层次分析法在太湖典型区域污染物总量分配中的应用

幸 娅，张万顺，王 艳，汤 怡

（武汉大学 资源与环境科学学院，湖北 武汉 430079）

1 研究背景

我国自“六五”期间开始实施污染物总量控制，实践证明其是控制污染源的发展趋势、改善环境质量和实现经济社会可持续发展的重要途径。实行总量控制，核心问题是各个排污单位或污染源之间如何科学、合理地分配区域允许的污染物排放量。目前，针对总量分配方法的研究，国外学者一般使用随机理论和系统优化相结合方法，Fujiwara等[1]基于概率约束模型，对允许排放的污染物总量在各个排污口间进行了分配。Burn等[2-3]依据概率约束条件，运用优化模型研究了这一问题。Li等[4-5]运用线性规划方法，Joshi等[6]采用直接推断法对排污口间污染物分配进行了研究。国内则主要是基于经济优化的原则采取的线性规划、非线性规划，以及基于公平性原则的等比例分配、按贡献率分配等方法[7]。但由于区域间在经济、环境、资源和管理等方面存在的差异性[8-9]以及排污总量控制系统所具有的不确定性[10]。忽视了这些因素，所制定的污染物总量分配方案和总量削减就难以达到预期效果。

本文遵循公平、有效、可持续发展的原则，从经济、社会和环境整体效益出发，考虑区域间社会、经济、环境、技术等多个因素，运用层次分析法构建了总量分配模型，选择常州市武进区作为太湖流域典型区域进行水污染物总量分配，并取得了较为满意的结果。

2 总量分配决策模型

公平、有效、可持续的总量分配应充分考虑分配区域在自然、社会、经济和技术等方面的差异，属于定量与定性相结合的一类问题。运用层次分析法把总量分配涉及的各种因素通过划分相互联系的有序层次使之条理化，根据对客观现实的判断，就每一层次中各因素的相对重要性给予定量表示，利用数学方法确定每一层次的各个因素的权重，为总量分配提供科学依据。

2.1 层次结构模型根据层次分析法的原则，将允许排放的污染物量作为目标层A，影响污染物总量分配的各分区的评价指标作为层次分析的准则层B、C，各个分区作为决策层D，建立层次系统结构模型，如图1所示。

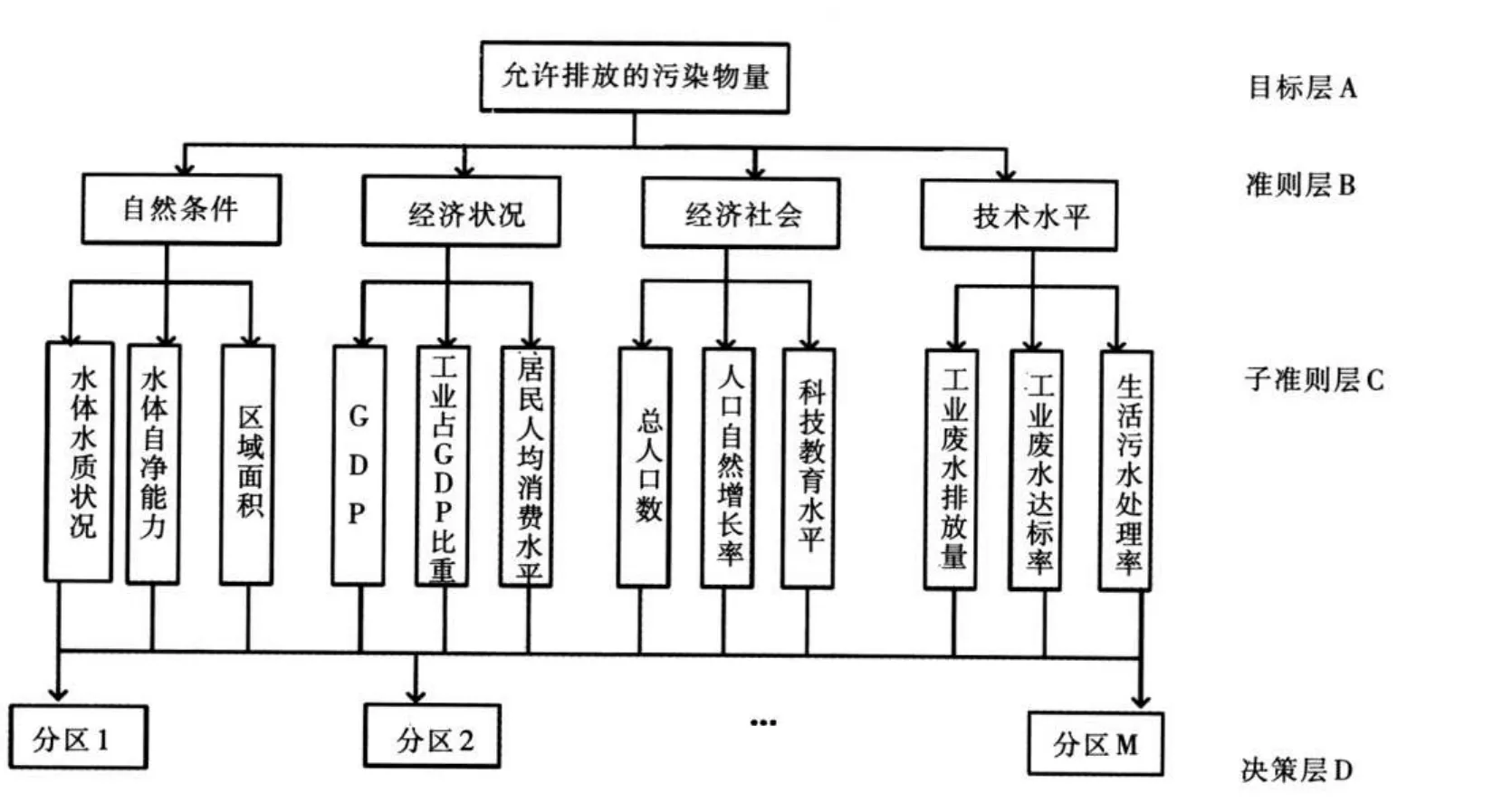
图1 总量分配层次结构模型

2.2 判断矩阵层次结构模型确定了上、下层元素间的隶属关系。对于同层各元素，以相邻上层有联系的元素为准，分别两两比较，在咨询有关专家意见的基础上运用评分办法判断其相对重要或优劣程度，一般采用1—9及其倒数的标度方法，见表1。

表1 1—9标度含义表

2.3 层次单排序及一致性检验用方根法计算各判断矩阵最大特征值λmax及其对应的特征向量。经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值，称为层次单排序。在评价的过程中，受到各种因素的影响可能产生判断的不一致性。为了测试评价判断的可靠性或不一致性，引入判断矩阵的最大特征值λmax和n之差与n-1的比值CI作为量度判断矩阵偏离一致性的指标，即用

若CR=CI/RI＜0.10，则说明判断矩阵一致性满足要求，即判断结果是可靠的。否则，应对判断矩阵的标度作适当的修正。1—9阶判断矩阵的RI值如下表所示：

表2 1—9阶判断矩阵的RI值

2.4 层次总排序及一致性检验计算同一层次所有因素对于最高层相对重要性的排序权值，称为层次总排序。这一过程是最高层次到最低层次逐层进行的。设WB=（w1，w2，…，wk）表示B层上k个元素相对于目标层A的排序权重向量。用Cj=（C1j，C2j，…，Cnj）表示C层上n个元素对B层第j个元素为准则的排序权重向量（其中无支配的元素权重取为0），则C层上元素对目标层A的组合权重向量为：

一致性检验也是从高到低逐层进行，如果B层次某些因素对于Aj单排序的一致性指标为CIj，相应的平均随即一致性指标为RIj，则B层次总排序随机一致性比率为：

类似的，当CR＜0.10时，认为层次总排序结果具有满意的一致性，否则需要重新调整判断矩阵的元素取值。

2.5 总量分配权重的确定分配区域指标基础数据归一化处理后，得出决策层D相对于目标层A的组合权重，该权重充分考虑了各分配区域的经济、社会、环境和技术等因素，因此视其为各分配区域占允许排放污染物总量的份额，即把各分配区域的组合权重作为各个区域的分配权重。

3 典型区域总量分配

3.1 典型区域基本资料选取太湖流域典型区域常州市武进区作为研究对象，实施污染物总量分配。常州市武进区境内河流纵横密布，形成北通长江，南连太湖、滆湖的自然水系。区内河道长2 100km。根据《常州市地表水（环境）功能区水资源质量状况通报》，在全区19个水功能区，监测断面22个，达标率为15.8%，2007年全区COD排放量为25 230t。区内河道水体水质不断恶化，以武进港、采菱港及中心区几条河流污染最为严重，基本为劣Ⅴ类，其余河流基本为Ⅴ类，水环境已不能承载区内经济社会的持续发展，实施总量控制刻不容缓。

3.2 分析计算

（1）运用层次分析法进行水污染总量分配研究，分别以常州市武进区湖塘、牛塘等16个乡镇构成决策层D，由于各个分区在自然属性和社会属性等方面存在客观差异，所以本文选取能够代表各个分区自然属性差异的水体水质状况、水体自净能力、区域面积，以及能够代表各个分区社会经济属性差异的GDP、总人口数、生活污水处理率和工业废水达标率等指标构成准则层B、C，基于流域水功能区水质目标，结合流域一维河网水质模型，确定流域允许排放的污染物总量为目标层A。

根据总量分配层次结构模型图，构建A-B，B-C判断矩阵，在咨询有关专家意见的基础上运用评分办法判断其相对重要或优劣程度，并进行层次单排序的一致性检验：

本文通过方根法计算最大特征根及其对应特征向量，计算结果如表3所示：

表3 判断矩阵计算结果

（2）准则层C相对于目标层A的层次总排序一致性检验：

一致性指标：

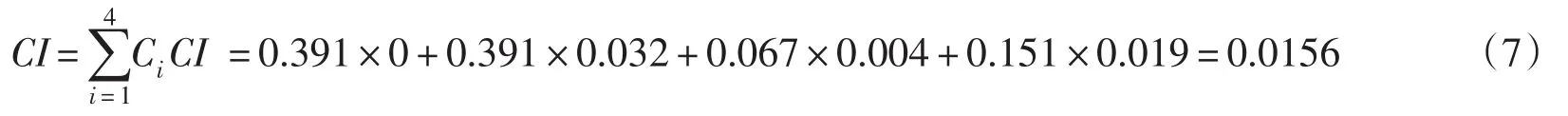
随机一致性指标：

判断矩阵一致性比率：

CR＜0.10，层次总排序结果具有满意的一致性。

（3）根据常州市武进区2007年的统计资料，构造决策层D相对于准则层C各元素的判断矩阵（C1-D），（C2-D），…（C12-D），求出各矩阵最大特征值及其相应的归一化后的权向量，再利用准则层C对目标层A的组合权重信息，见表3，求出决策层D对目标层A的总排序权重，所得结果见表4。

表4 各单元分配权重

从表中可以看出高新区、湖塘镇、横山桥镇等分配权重较大，分别为0.128、0.112和0.079。奔牛镇，经发区分配权重较小，分别为0.037和0.017。由于各分区对总目标的组合权重，是在较为全面地考虑了各分区经济、社会、环境和技术等条件的基础上得出的，因此，可将其视为各分区对允许排污总量占有份额的表示。分配结果与现状排放量对比如图2，图3所示。

分配后结果显示：湖塘镇、郑陆镇和横林镇3个单元COD现状排放量较大，分别为15 715.6、14 254.6和14 102.25kg/d。由于湖塘、郑陆和横林3镇的现状排污量较大，水质状况较差，并考虑3镇社会经济、人口以及科学技术发展水平，利用层次分析法确定分配权重，分配后3个单元的允许排放量为6 667.84、4 675.16和4 064.75kg/d，3个单元的削减比例分别为：57.6%、67.2%和71.2%。除高新区以外，各单元现状排放量略大于分配后的允许排放量，需要削减的比例较小。高新区现状排放量为6 277.23和7 630.73kg/d，在现有基础上可以增加水污染物排放量。

NH3-N分配结果与COD分配结果相似，湖塘镇、郑陆镇和横林镇3个单元COD现状排放量较大，分别为：1 089.07、981.07和552.08kg/d，分配后3个单元的允许排放量为：458.91、321.77和279.76kg/d。其他各单元现状排放量与分配后的允许排放量相差较小。其中，横山桥镇现状排放量与分配后的允许排放量分别为283.85和277.22kg/d。高新区现状排放量为：432.03kg/d，分配后的允许排放量为525.19kg/d，在现有基础上可以增加水污染物排放量。

图2 COD分配后与现状排放量对比

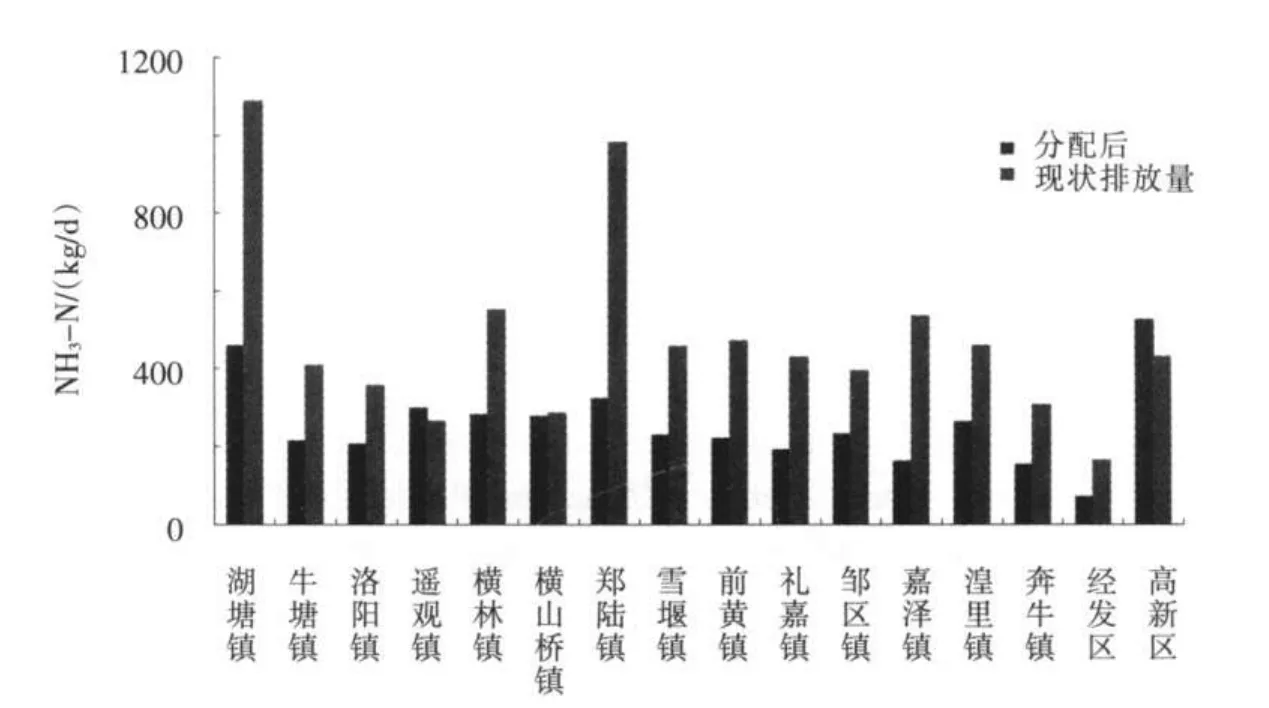
图3 NH3-N分配后与现状排放量对比

4 结论

本文在考虑了区域之间的经济、社会和环境差异的基础上，通过构建总量分配指标体系和矩阵模型，计算出各单元的排污权重大小，对其排污量进行分配。与一般的等比例削减方法或按贡献率削减方法相比，运用层次分析法进行污染物的总量分配层次分析法比较全面地考虑了影响污染物总量分配的各种因素，体现出单元之间的区域差异因素。解决了影响总量控制分配因素众多带来的不确定性问题，提高了污染物总量分配的科学性，更趋合理。评判指标值的选取、权重的确立及评判模型的选定，指标选取的合理与否都会影响到总量分配结果。

[1]Fujiwara o，Gnanendran S K，ohgaki S.River qual ity management under stochast ic stream flow[J].Environ.Eng.，1986，112（2）：185-198.

[2]Burn D H，Mcbean E A.Optimization modeling of water quality in an uncertain environment[J].Water Resour.Res.，1985，21（7）：934-940.

[3]Burn D H，Lence B J.Comparison of optimization formulations for waste-load allocations[J].J.Environ.Eng.，118（4）：597-612.

[4]Li shiyu，Tohru Morioka.Optimal allocation of waste loads in a river with probabilistic triburary flow under transverse mixing[J].Water Environment Research，1997，71（2）：156-162.

[5]Li shiyu.A programming model for river quality management under transverse mixing[J].Water Sci.Tech.，1992，26（7-8）：1823-1830.

[6]Joshi V，Modak P.Heuristic algorithms for waste load allocation in a river basin[J].Water Sci.Tech.，1989，21：1057-1064.

[7]胡国华，赵沛伦，王任翔.黄河盂津一花园口河段水环境容量研究[J].水资源保护，2002，1：26-30．

[8]张玉清.河流功能区水污染物容量总量控制的原理和方法[M].北京：中国环境科学出版社，2001：2-9.

[9]杨玉峰，傅国伟.区域差异与国家污染物排放总量分配[J].环境科学学报，2001（2）：129-133.

[10]杨玉峰.污染物排放总量控制系统的不确定性分析[D].北京：清华大学，1999.