基于数值流形元法的混凝土力学特性数值试验

赵 妍，张国新，林易澍，武晓川

（1.中国水利水电科学研究院 材料结构研究所，北京 100038；2.河海大学 水利水电工程学院，江苏 南京 210029；3.北方国际合作股份有限公司，北京 100053）

1 研究背景

混凝土是工程中广泛应用的一种材料，在细观层面表现为多相非均质性。目前进行混凝土力学试验是研究其力学特性最基本的方法，但是力学试验需要花费大量的人力、物力，所得到的试验结果又往往与试验条件、环境条件等的变化及材料本身的复杂性有关，使得试验成果相对离散。数值试验是近些年发展起来的一种新的方法，采用非线性方法，通过对数值试件细观层面的力学特性的精细模拟，可以得到试件宏观力学性质。数值试验方法可以避免一些不确定因素的影响、可在电脑上进行大量的重复试验、可以节省大量的人力物力。因此宏观与细观相结合，以基本物理试验数据和静动力学理论为基础，用数值方法模拟混凝土细观结构裂纹产生、扩展及与宏观力学性能关系的细观力学已经发展起来，成为20世纪90年代重要研究方向之一。

在细观层次上，混凝土是由粗骨料、水泥水化物及骨料与水泥砂浆黏结带（界面）等细观结构组成的多相复合材料。为了对各相材料的力学性质进行细观力学数值模拟，人们提出了许多研究混凝土断裂过程的细观力学模型[1]。最具典型的有格构模型（Lattice model）、随机粒子模型（Random particle model）、Mohamed A R等提出的细观模型、随机骨料模型（Random aggregate model）、唐春安等人提出的随机力学特性模型以及马怀发提出的随机骨料随机参数模型等，这些细观模型各具优缺点。

目前从细观层次上模拟混凝土断裂，大多都是基于有限元完成的。1996年前后，王宗敏首先用精细网格有限元模拟混凝土的破坏，当单元受拉破坏后，将单元去掉，该方法建大实用，但是这带来了质量和能量的不守恒，只能模拟混凝土的拉裂破坏。2004年，朱万成等[2]等利用开发的MFPA2D进行了混凝土细观力学性质对宏观断裂过程影响的数值试验，该系统仅考虑了混凝土各相材料力学特性分布的随机性，未考虑混凝土粗骨料颗粒分布的随机性。

于庆磊等[3]等应用数字图像处理技术，在细观上表征混凝土材料中由骨料的形状、大小和分布对混凝土材料造成的非均匀性；采用统计力学方法描述材料的非均匀性，模拟了混凝土单轴荷载作用下的破坏过程。马怀发等[4]等在随机骨料模型的基础上提出了随机骨料随机参数模型。该模型不仅考虑了骨料按级配随机分布，而且考虑了混凝土及其细观各相单元的抗拉强度和弹性模量均为随机参数，遵循对数正态分布。由于目前的数值试验难以模拟界面的接触非线性和界面的压剪破坏，因此只能模拟拉裂破坏。

石根华提出的数值流形元法[5]为混凝土断裂的模拟开辟了新的途径。该方法充分吸收了DDA的块体模拟和接触模拟的优点，用一套物理网格定义和处理块体边界及构造面，可以很好地模拟块体接触运动，离散体大位移问题。同时用一套数学网格定义块体内部的位移插值函数，可以像有限元那样计算块体内部的应力。张国新[6-10]对石根华的数值流形法进行了较大的扩展，使流形法可以模拟结构的剪断、完整块体内裂纹的生成及多裂纹的追踪等。

本文从细观角度出发，假定混凝土为由砂浆基质、骨料组成的多相复合材料，借助蒙特卡罗方法，在试件截面上随机确定骨料的位置、形状和尺寸，产生出随机骨料模型。利用改进的流形元法特有的两套网格和完善的一整套接触搜索的方法，以及裂纹自动搜索追踪的功能，模拟多裂纹扩展、贯通等相互作用的特有优势，来进行混凝土断裂过程的模拟，研究混凝土力学特性以及其断裂机理。

2 数值流形法的破坏模拟

结构的破坏形式主要有两种：一是沿薄弱部位，如节理、裂隙、软弱夹层、混凝土结构的构造缝等，这类破坏的模拟要求数值方法不仅能正确计算沿界面的接触应力，还得能模拟界面的张开，滑移等，并且当带有抗拉、抗剪强度时，要能模拟沿界面的破坏过程。二是在连续介质中的破坏形态，模拟这类介质的破坏以裂纹的产生和扩展为主，同时可以模拟连续介质的剪切破坏。本文作者开发的流形元程序可以模拟以上两种情况。

流形元模拟沿已有结构面破坏时，采用带抗拉强度的摩尔-库仑准则。当沿构造面的法向应力和切向应力σn满足τs下式时，构造面破坏。

剪切破坏：τs=c，当且σn＜0且σn＜σc

式中：σn压为正，拉为负；φ为摩擦角； σc为抗拉强度；c为凝聚力。

式（1）模拟沿界面的张开破坏；式（2）模拟岩界面的剪切破坏。

连续介质内新裂纹的产生按抗拉强度准则，新裂纹的扩展遵循断裂力学应力强度因子准则。断裂力学认为，裂缝的扩展并不取决于缝端的应力大小，而是取决于缝端的应力集中程度，即应力强度因子或应变能。当缝端的应力强度因子达到某临界值时，裂缝开始扩展，该临界值称为断裂韧性。本文计算裂缝扩展首先用作者开发的二阶流形元程序求解含裂纹体的位移、应力场，然后围绕缝端切出一含有缝端的局部子域，将用流形元法求出的该子域周边的位移作为已知位移边界条件，利用考虑了缝端奇异的奇异基本解和Kelvin基本解构造出边界积分方程，用边界元法求解，求出缝端应力强度因子[8]。求出应力强度因子后，用最大周向应力准则判断裂缝是否扩展及扩展方向。根据该准则，开裂角θ0决定于方程：

由上式得出开裂角：

最大周向应力理论建立起来的I—Ⅱ复合裂纹的断裂判据：

式中：θ0为裂纹扩展方向与初始裂纹的夹角。

石根华在流形法中开发的一套接触模拟方法，可以精确的计算结构面的接触力，二阶流形元法和奇异边界元法结合可以精确求解缝端的应力强度因子。因此用扩展的数值流形法来算破坏模拟，可以正确模拟带岩桥岩体的破坏。裂纹产生、扩展后不用重新剖分网格，只需改变相应的物理边界和数学覆盖即可，具体实现方法参照有关文献[5]。

3 数值流形法的裂缝追踪技术

进行混凝土力学特性的试验，往往伴随多条裂纹的出现，因此对于多裂纹的模拟是至关重要的。本文用子域奇异边界元法求解裂纹应力强度因子的模拟方法，详细步骤见文献[10]。

本文的流形元法引借助断裂力学方法结合奇异边界元法模拟破坏，解决了裂纹可以沿任意方向扩展和群缝追踪问题。具体多裂缝追踪技术可分为如下几步：（1）同时追踪所有的缝端，判断是否有满足开裂准则，并求出开裂安全系数；（2）允许开裂安全系数最小者扩展；（3）如没有裂缝扩展，搜索所有的节点，判断是否有节点满足新裂缝产生准则；（4）允许满足准则且安全系数最小的节点产生新裂缝，然后重复上述步骤，进行下一个循环。

4 混凝土力学特性数值试验的流形元模拟

基于对混凝土细观结构的认识，假定混凝土是由砂浆基质及骨料组成的多相复合材料，它们之间的界面层以试验为基础赋予相应的参数来模拟，考虑各相组分的非均匀性，利用蒙特卡罗方法、Fuller级配公式建立用于流形元模拟的细观模型，利用前面介绍的扩展的流形元法本身特有的两套网格和完善的一整套接触搜索的方法，以及裂纹自动搜索追踪的功能，模拟多裂纹扩展、贯通等相互作用的特有优势，来进行混凝土力学特性的数值试验模拟，展示在混凝土细观结构之下，利用数值流形元方法模拟混凝土的断裂的详细过程以及其断裂机理。

4.1 随机骨料模型由于蒙特卡洛方法由于能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果，本文采用它建立用于流形元模拟的随机骨料模型。

为了确定骨料所占的面积，可假设骨料最大直径为Dmax，最小直径为Dmin，直径小于Dmin的骨料归为砂浆，则直径在[Ds，Ds+1]范围内骨料所占面积Aagg由下式可得：

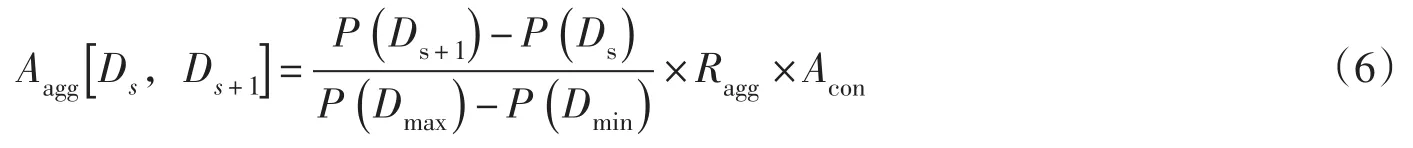
式中：P(Dmax)、P(Dmax)分别为最大骨料和最小骨料所占面积的累积概率；P(Ds+1)、P(Ds)分别表示骨料直径为Ds+1和 Ds所占面积的累积概率。

Walraven J.C.基于Fuller公式，将三维级配曲线转化为试件内截平面上任一点具有骨料直径D＜D0的概率PC（D＜D0），其表达式为：

式中：Pk为骨料体积占试件总体积的百分比，一般取Pk=0.75；Dmax为骨料最大粒径。由该级配浇筑的混凝土可产生优化的结构密度和强度来决定。

图1给出了产生的随机骨料模型，模型剖面为100×100mm的正方形。图中粗骨料的最小和最大直径分别取为5mm和20mm。

图1 随机骨料模型

从图中可以看出，骨料占有率对产生骨料的数量以及随机分布都有很大的影响；砂浆的最小厚度γ会影响骨料相对间的摆放位置。

4.2 混凝土单轴受压破坏过程的流形元模拟模拟单轴的混凝土试件，粗骨料为普通的碎石，最大直径为20mm，抗压强度为35MPa（单轴抗压强度），具体参数如表1所示。

表1 混凝土试件的力学参数

模拟中采用与试验室试验一样的加载方式，上端采用位移控制的加载方式，加载速度为0.000 05m/s，下端水平方向固定，混凝土受压破坏加载模型见图2。图3给出了混凝土试件在加载不同时刻的混凝土断裂形态图。

图2 混凝土受压破坏加载模型

图3为受压破坏不同时刻混凝土试件的断裂过程，其中细线代表未破坏的界面，粗线代表界面已经破坏。在加载的初始阶段，应力较小，骨料界面因强度较低，首先破坏，接着混凝土中也出现一些小裂纹，这些界面的破坏以及裂纹的出现，使整个试样产生应力重分布，在它们的周围形成应力集中，进而周边单元产生较大的拉应力，引起裂纹扩展以及新的裂纹产生。随着外荷载的不断增加，不断有界面破坏以及新的裂纹产生，裂纹开始相互贯通。在试件达到峰值荷载时，由于试件内部的破坏，承载力已经达到极限，在增加外部施加的位移时，裂纹带形成，如图3（e）所示，宏观裂纹基本沿荷载加载方向，绕过骨料沿着砂浆介质扩展，由于骨料强度较大，有些裂纹遇到骨料止裂。此后由于试件承载力的降低，试件中裂纹稳定扩展，周边也出现新的裂纹，直至失去最后的承载力，如图3（h）所示，试件破坏。

研究还发现，在单轴受压情况下，裂缝的扩展方向不是直线和连续的，出现裂纹交错分叉的现象，这是由于混凝土的不均匀性带来的。

图3 混凝土受压破坏断裂过程（数值模拟结果）

由图4可以看出，加载初期，由于荷载较小，应力—应变仍保持着较好的线性，随着荷载的增大，不断有裂纹出现，应力的增加小于应变的增加，曲线出现明显的非线性。随着荷载的增加，裂纹开始贯通，曲线非线性更加明显，应力逐渐达到峰值。到达峰值后，试件发生失稳，但保留较大的残余强度，逐渐失去承载力，直至试件完全断裂。

图5为混凝土试样单轴抗压强度的试样。可以看出流形元模拟得到的破坏模式和裂纹形态也和试验结果表现出很好的相似性。说明流形元模拟结构破坏，裂纹扩展等方面是正确的。

图4 混凝土受压破坏应力-应变曲线

图5 混凝土试样单轴压缩荷载下的破坏形态

从以上结果可以看出，扩展的流形元对这种含有多结构面的混凝土细观结构的断裂过程模拟是非常准确的，而且破坏后产生的多裂纹扩展问题也能很好的追踪，可以很好的模拟混凝土试件的断裂过程，可以部分代替试验研究，这解决了以往数值方法都不能很好解决的问题。

4.3 混凝土单轴受拉破坏过程的流形元模拟本节采用图1中所示的模型，顶部施加拉伸位移，速度为0.000 05m/s，骨料与砂浆界面抗拉强度Re=3.0MPa，用扩展的二阶流形元模拟其断裂过程，图6-图8为得到的混凝土的断裂模拟结果。

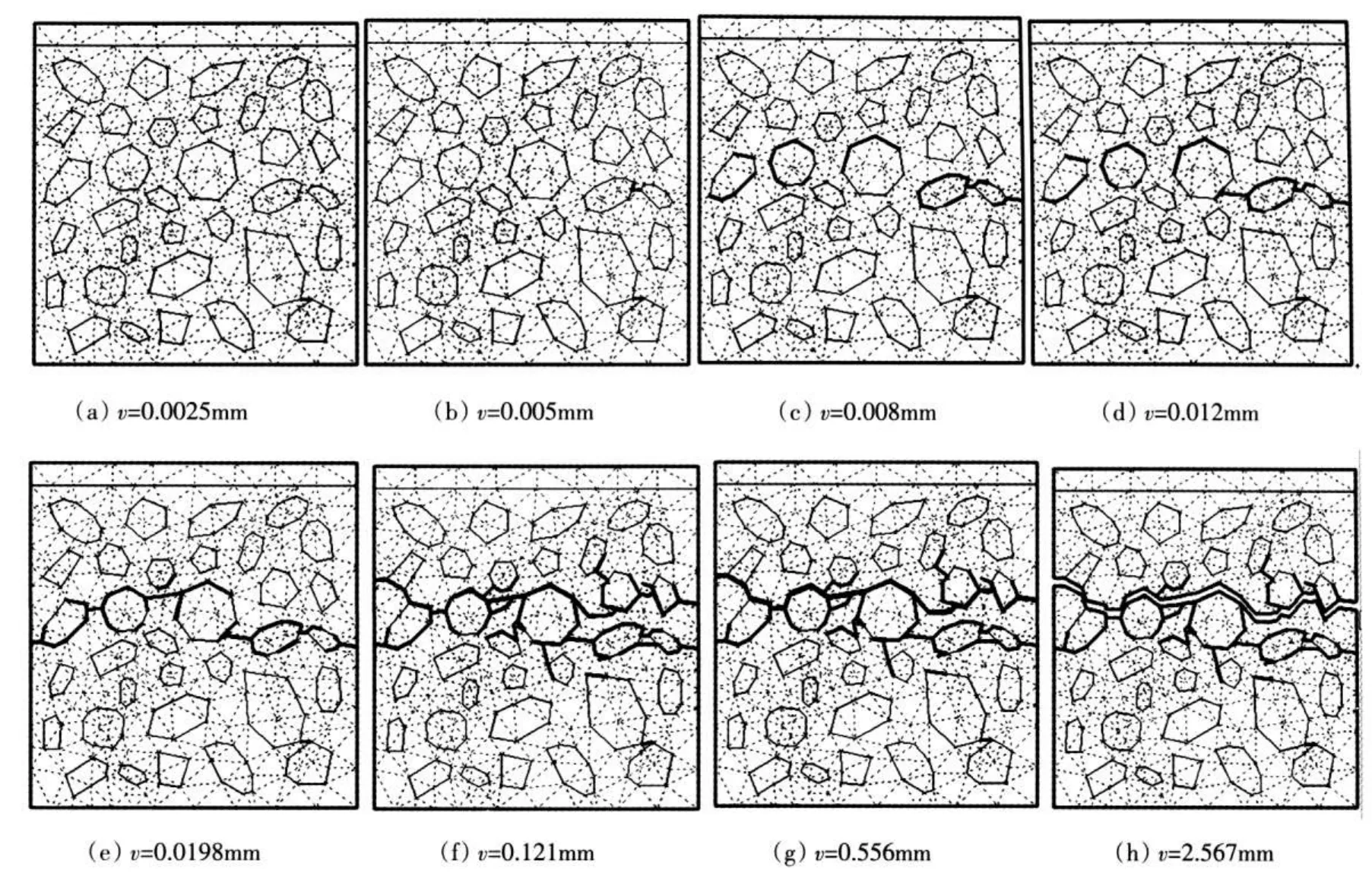
图6 混凝土单轴受拉破坏断裂过程

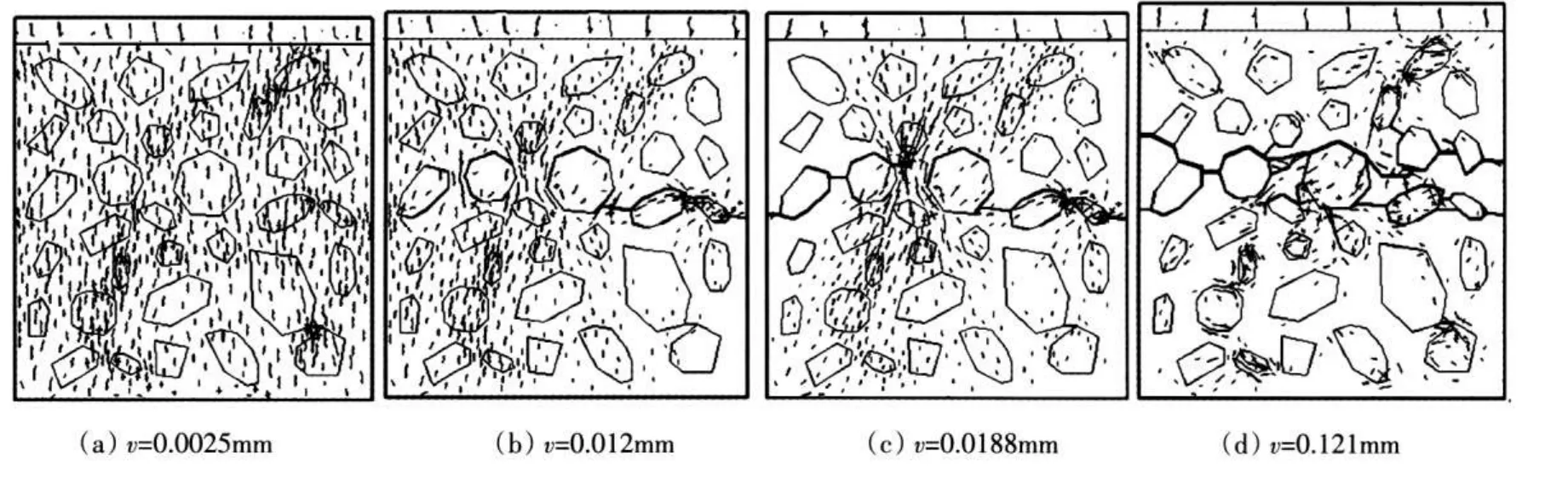
图7 混凝土单轴受拉破坏应力向量

从图6、图7可以看出，混凝土受力主要为拉应力，其宏观裂纹的方向垂直于位移加载方向，主要表现为横裂纹。加载初期，数值试件骨料与砂浆的界面首先破坏，进而这些裂纹向砂浆基质中不断扩展，变形局部化逐渐表现出来，最后形成一条或多条大致垂直与拉伸荷载作用方向的宏观裂纹。由于考虑了混凝土材料的非均匀性，加载初期，宏观裂纹的路径往往呈现曲折性，绕过骨料，在界面和砂浆基质中扩展。图8应力-应变曲线呈现出明显的非线性特性。

图9为试验得到的单轴受拉试件的破坏试件，形成的宏观裂纹大致垂直于主拉应力的方向，沿着砂浆或骨料与砂浆之间的界面破坏。这与数值模拟结果得到的裂纹扩展从砂浆和骨料的界面开始，裂纹的扩展方向基本上绕过骨料，并且不是直线和连续的相符合。

4.4 不同界面强度的影响研究混凝土中砂浆与骨料的界面强度对混凝土强度影响较大，因此界面抗拉强度分别取0.3、1.0、2.0和3.0MPa，分别对4.3节中的单轴受拉试件进行数值模拟，研究不同的界面抗拉强度对混凝土整体宏观强度的影响。

当骨料与砂浆界面取不同的抗拉强度时，裂纹出现的时刻和位置是不同的；在同一加载时刻，抗拉强度越大，裂纹出现越迟，试件破坏程度越低，这说明骨料与砂浆的抗拉强度程度对于混凝土整体强度有很大的影响，因此浇筑灌浆时，增加其黏结程度，对提高混凝土的抗拉能力是有很大作用的。

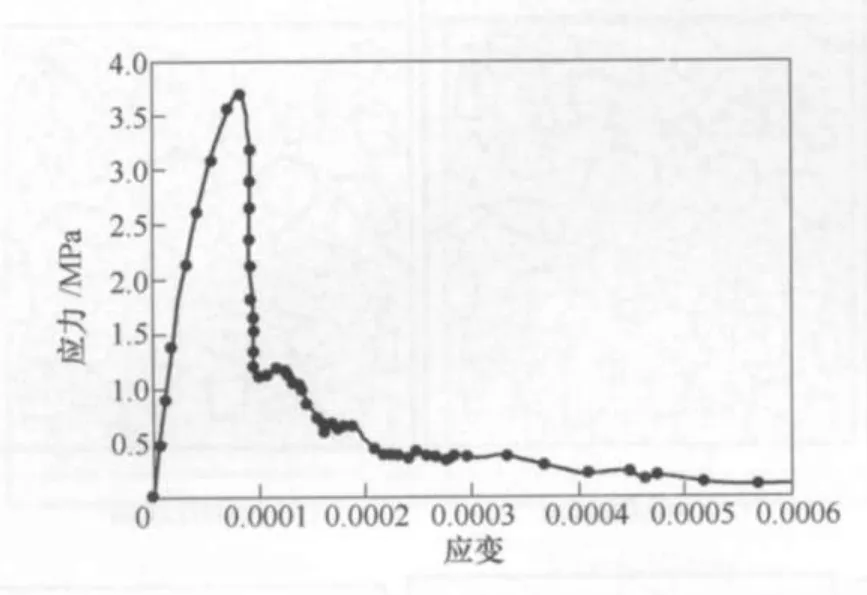
图8 混凝土单轴受拉破坏应力-应变曲线

图9 受拉试件试验破坏断面

图10为流形元模拟得出的各界面间取不同凝聚力时应力-应变对比曲线，从图中可看出，提高界面的抗拉强度，可以使混凝土强度有很大提高，非线性趋势也更加明显，峰值过后应力值下降较缓慢。说明界面的抗拉强度对提高混凝土宏观整体强度有一定的帮助。因混凝土是准脆性材料，其应力-应变曲线整体脆性较为明显。这些结果符合试验的结果。可以说本文建立的数值试样，可以很好的反映混凝土的细观结构，扩展的流形元方法因其有一整套模拟裂纹追踪和扩展的功能，可以很好的模拟其断裂过程及其力学特性。

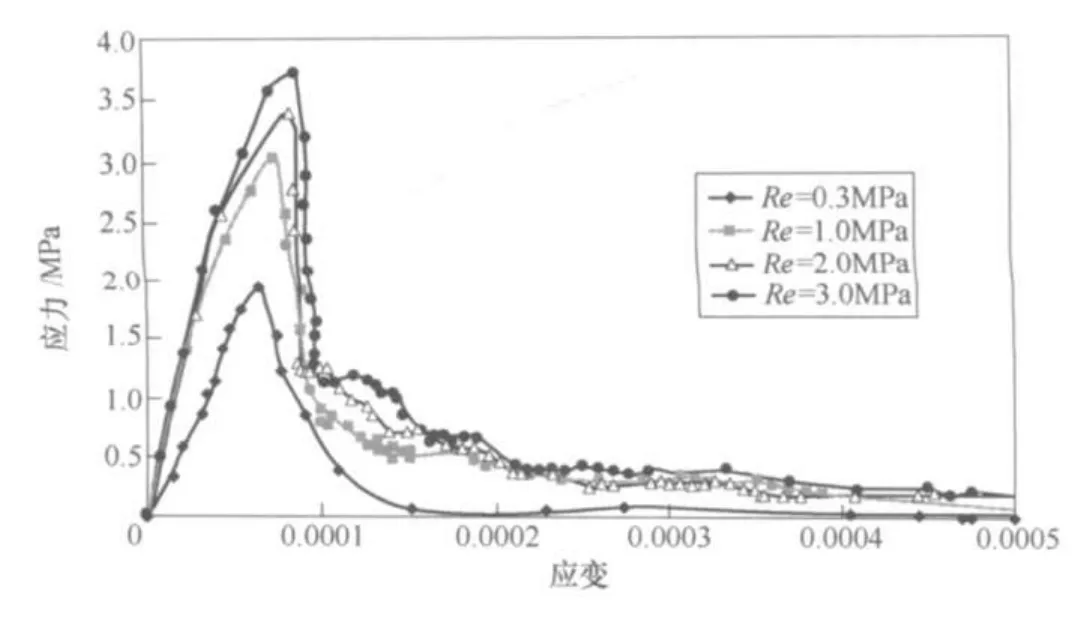
图10 界面间取不同凝聚力时单轴拉伸应力-应变曲线对比

5 结论

从细观层次出发，把混凝土看作是由砂浆基质、骨料的二相复合材料，为了考虑各相组分的非均匀性，借助蒙特卡罗方法，建立了随机骨料模型。用研究开发的可用于材料破坏过程分析的二阶流形元法对混凝土细观数值模型单轴压缩、拉伸等试验进行模拟，得出了试件的破坏模式以及应力-应变曲线，也证实了黏结带的力学性质对于普通混凝土的宏观断裂过程起重要作用。其模拟得出断裂过程的现象与试验结果具有相似性，应力-应变曲线表现出明显的非线性，与实际相符，证明开发的二阶流形元方法对混凝土材料在各种受力条件下的断裂过程及以及混凝土材料的力学性能研究是颇为有前途的方法。

[1]马怀发，陈厚群，黎保琨.混凝土细观力学研究进展及评述[J].中国水利水电科学研究院学报，2004，2（2）：124-130.

[2]朱万成，唐春安，滕锦光，等.混凝土细观力学性质对宏观断裂过程影响的数值试验[J].三峡大学学报（自然科学版），2004，2（1）：22-26.

[3]于庆磊，唐春安，朱万成，等.基于数字图像的混凝土破坏过程的数值模拟[J].工程力学，2008，25（9）：72-78.

[4]马怀发，陈厚群.全级配大坝混凝土动态损伤破坏机理研究及其细观力学分析方法[M].北京：中国水利水电出版社，2008.

[5]石根华.数值流形方法与非连续变形分析[M].裴觉民译.北京：清华大学出版社，1997.

[6]Zhang G X，Yasuhito Sugiura，Kozo Saito.Failure Simulation of Foundation by Manifold Method and Comparison with Experiment[J].Journal of Applied Mechaics，JSCE，1998，1：427-436.

[7]张国新，彭静.二阶流形元与结构变形分析[J].力学学报，2002，34（2）：261-269.

[8]张国新，金峰，王光纶.用基于流形元的子域奇异边界元法模拟重力坝的地震破坏[J].工程力学，2001，18（4）：18-27.

[9]张国新，赵妍，等.考虑岩桥断裂的岩质边坡倾倒破坏的流形元模拟[J].岩石力学与工程学报，2007，9：1773-1780.

[10]张国新，赵妍，石根华，等.模拟岩石边坡倾倒破坏的数值流形法[J].岩土工程学报，2007，29（6）：800-805.