电力线载波通信报文压缩技术研究
蒋觐阳,曹 亮
兰州大学信息科学与工程学院,甘肃兰州 730000
电力线载波通信是利用已有的电力线路进行数据传输的一种通信方式,无需专门架设通信基础设施并且具有相当广泛的网络分布,具有投资小、设备简单、通信可靠性高等优点。然而,由于电力线载波通信存在着一些技术难题,如传输信道间歇噪声大、阻抗随负载变化大、信号衰减大等问题,我们将数据压缩技术引入电力线载波通信,在数据传输前进行压缩,这样就可以尽可能在有限的带宽内传输尽可能多的数据。
1 数据压缩原理
数据压缩是指在不丢失信息的前提下,缩减数据量以减少存储空间,提高其传输、存储和处理效率的一种技术方法。或按照一定的算法对数据进行重新组织,减少数据的冗余和存储的空间。压缩的理论基础是信息论[1]。从信息的角度来看,压缩就是去除掉信息中的冗余,即去除掉确定的或可推知的信息,而保留不确定的信息,也就是用一种更接近信息本质的描述来代替原有的冗余的描述,这个本质的东西就是信息量。
关于数据压缩有很多算法,针对不同特点的数据选择不同的压缩算法从而达到最优的压缩效果。LZW继承了LZ77和LZ78压缩效果好、速度快的优点,且算法描述易于接受。该算法能在不了解数据统计特性前提下,使压缩比接近已知统计特性时所能达到的压缩比,且易于实现,是目前最常用的算法。
1.1 LZW算法基本原理
LZW压缩算法是一种新颖的压缩方法,Lemple-Ziv-Welch 三人共同创造,用他们的名字命名。它采用了一种先进的串表压缩,将每个第一次出现的串放在一个串表中,用一个数字来表示串,压缩文件只存贮数字,则不存贮串,从而使图像文件的压缩效率得到较大的提高。奇妙的是,不管是在压缩还是在解压缩的过程中都能正确的建立这个串表,压缩或解压缩完成后,这个串表又被丢弃[2]。
LZW算法中,首先建立一个字符串表,把每一个第一次出现的字符串放入串表中,并用一个数字来表示,这个数字与此字符串在串表中的位置有关,并将这个数字存入压缩文件中,如果这个字符串再次出现时,即可用表示它的数字来代替,并将这个数字存入文件中。压缩完成后将串表丢弃。如"print" 字符串,如果在压缩时用266表示,只要再次出现,均用266表示,并将"print"字符串存入串表中,在图像解码时遇到数字266,即可从串表中查出266所代表的字符串"print",在解压缩时,串表可以根据压缩数据重新生成。
LZW算法流程:
1)初始化:将所有的单字符串放入串表;2)读第一个输入字符给前缀串ω;3)Step: 读下一个输入字符K。
if 没有这样的K(输入已穷尽):
码字(ω) 输出;结束。
If ωK 已存在于串表中:
ω:=ωK;repeat Step;
else ωK不在于串表中:
码字 (ω) 输出 ;
ωK加进串表;
ω:=K;repeat Step.
例子:
input:ababcbababaaaaaaa
ω:a->ab->ba->ab->4c->cb->ba->5b->8a->aa->aa->10a->aa->11a->a#->#
串 表:1(a) 2(b) 3(c) 4(ab) 5(ba) 6(4c) 7(cb) 8(5b) 9(8a) 10(aa)11(10a) 12(11a)
output:a b 4 c 5 8 a 10 11 a
1.2 电力线通信报文压缩算法设计
将LZW压缩算法应用在电力线通信中,数据采样利用率提高了两倍,使报文传递更可靠;通过控制信息位(bit)级检错、数据信息分组检错等手段,增强检错能力,降低误同步概率;数据信息分组检测纠错,报文长度不再受链路层程序逻辑限制;纠错方式不再是唯一的扩频,支持不同长度的扩频编码,速率的提高可减少报文冲突几率,有利于并行路由的顺畅运行;报文压缩后不仅可以提高传输速率,还可以提升数据传输成功机率[3]。
例如,报文原始数据为:255,24,54,255,24,255,255,24,5,123,45,255,24,5,24,54...如何对它进行压缩,因为原始数据可以用8bit来表示,故清除标志Clear=255+1 =256,结束标志为End=256+1=257,目前标号集为0 1 2 3......255 CLEAR END
第一步,读取第一个字符为255,在标记表里面查找,255已经存在,不做处理;
第二步,取第二个字符,此时前缀为A,形成当前的Entry为(255,24),在标记集合不存在,把它在标记集合中标记为258,然后输出前缀A,保留后缀24,并作为下一次的前缀(后缀变前缀);
第三步,取第三个字符为54,当前Entry(24,54),记录(24,54)为标号259,并输出24,后缀变前缀;
第四步:取第四个字符255,Entry=(54,255),记录(54,255)为标号260,输出54,后缀变前缀。.......
一直处理到最后一个字符,用一个表记录处理过程,CLEAR=256,END=257。
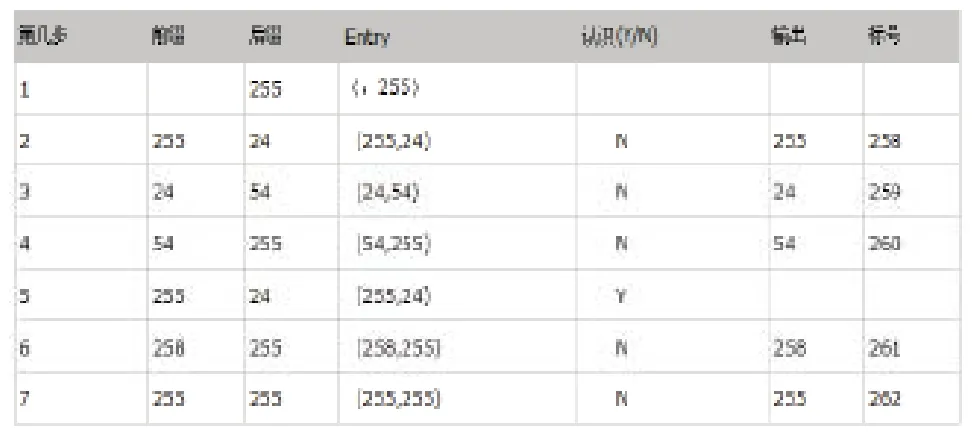
表1 LZW算法举例
2 算法改进
2.1 改进思路
LZW方法简单易行,但是存在诸多不足,例如,对不同大小的文件,均使用12位输出代码。在压缩的开始阶段文件较小时,字典中的短语比较少,使用位数更少的压缩代码显然能减少压缩文件的大小[4]。当“next code”的值在256到511之间时,9位输出代码就足以表示所有短语;另一个有待改进的方面是压缩率的监测。在压缩进程中,当字典空间被填满、新的短语不能加入到字典中时,对随后的字典中无定义的字符串就无法进行压缩,压缩率将下降。
2.2 改进方法
1)可变代码长度
发现字典填满时,立即将字典清空,以便后续字符串能建立短语。首先在字典中设置清除标志,当字典填满后,在进行阈值判断时,对每一个码字(Code Word)的使用情况计数。当进行阈值判断所得到的压缩比小于指定的阈值时,发出清除标志,这时根据字典中每一个码字使用的计数值大小进行排序,对字典进行相应的重构,然后删除排序靠后的若干项。这种方法较简单,也有效果[5]。
STEPl初始化,使开始词典包含所有可能的根(Root),当前前缀P置空;
STEP2当码字流有码字要译时,反复执行STEP3,STEP4,STEP5和STEP6;
STEP3读入字符数据流中的下一个字符C;
STEP4如果字符串P+C在当前词典中,
a P置P+C(用字符C扩展P);
b 把代表当前前缀P的码字输出到码字流;
否则,
c 输出表示P的码字到编码数据流;
d 把字符串P+C添加到词典;
e P置C(此时P仅含一个字符C);
STEP5若字典未满,则执行STEP3;
STEP6如果压缩比小于指定阚值,则清除匹配率小的词条,否则,返回STEPl;
STEP7结束。
2)监测压缩率
要监控压缩率的变化至少需要知道四个量。一是原始压缩率,显然压缩率为100%。二是现在的压缩率,由输出压缩代码与输入字符数的比值来确定,必须知道输入字符数和输出压缩代码。以上四个变量在程序中分别定义为ratio_old、ratio_new、bytes_in、bytes_out。其中
ratio_new=
当程序通过ratio_new值发现压缩率已经低于100%,说明字典中的短语已经过时,不再适合压缩之用,应建立新的字典。这里选择在输入字符号每增加一百个时计算一次,用一个标识通知还原算法原来的字典已经不再使用,还原算法即可从此开始建立新字典。压缩程序改进如下:
while((character=getc(input))!=(unsigned)
EOF){
++bytes_in;/*计算输入值*/
if(bytes_in>checkpoint){/*checkpoint初始值为100*/
if(num_bits==MAX_BITS){
ratio_new=bytes_out*100/bytes_in;∥计算新压缩率
if(ratio_new>ratio_old){/压缩率是否下降
OutputBits(output,CLEAR_TABLE,code_bits);//输出标识
code_bits=9;//压缩代码位数从9开始
next_code=258;∥短语从258开始编码
dict_byte=511; ∥字典容量为512
bytes_in=bytes_out=0; ∥ 复 位 bytes_in、bytes_out ratio_old=100;
for(i=0;i code_value[i]=一1;} else/*压缩率没有下降*/ ratio_old=ratio_new;∥以ratio_new作为ratio_old,以便下次比较 还原程序改进如下: while((new_code=input_code(input))!=END_OF_STREAM) { if(new_code== CLEAR~TABLE){ /*清空字典标识*/ code_bits=9;∥压缩代码位数从9开始 next_code=258; ∥短语从258开始编码 dict_byte=511; ∥字典容量为512 continue; }…… 给出算法比较图 表2 LZW经典算法与改进算法压缩性能比较 首先,由表中数据可以看出改进的LZW算法对各种不同类型的文件压缩率都有了很大的提高,特别是对位图文件的压缩率改善更加显著。 其次,改进的LZW算法不仅压缩比较高,且压缩用时也较短,在电力线载波通信中,报文数据经过压缩,可以让出带宽,达到最初设想。 [1]袁枚.数据压缩技术及其应用[M].北京:电子工业出社,1995. [2]Mark Nelson.数据压缩技术原理与范例[M].北京:科学出版社,1995. [3]周天晖,王光.改进的LZW压缩算法在语音数据复接器中的应用[J].电力系统通信,2002(12). [4]刘萌,丁香乾.电力线窄带通信报文压缩算法研究[J].网络与通信,2010(16). [5]ZIV J,LEMPEL A.A universal algorithm for sequential data compression[J].IEEE Transactions on Information Theory,VOL.1T一23,NO.3,MAY 1977.3 改进的LZW算法比较


