基于复合Newton-Cotes改进的一种数值积分算法

刘 浩,李梦爽

南京大学，江苏南京 211102

1 问题的提出

[1]中的证明可知：在 n<=8 时数值稳定，误差随n 的增大而减小，同时n>8 时，会产生数值不稳定性，造成巨大计算误差。但是，实际的计算过程中误差并没有像[1]中所言在n小于8时候会随着n的增大而减小，而是减小到一定程度之后就不再减小。

经过实验分析（在精度更高的计算环境下，误差的减小微乎其微）我们确定这不是由于计算机表示精度的原因造成的。进一步分析和对比[2]中的给定积分系数Ai，我们确定这是由于其中在计算过程中计算Ai多项式积分引入了额外的误差。于是我们提出了一种改进的Newton-Cotes数值积分算法。我们称新算法为后置秦氏Newton-Cotes算法。

2 算法的介绍

经典的复合Newton-Cotes算法和相关结果

Newton-Cotes计算方法是将问题转化为计算积分的近似值

当阶数过大时会产生数值不稳定性，所以采用复合Newton-Cotes算法增加计算的精度。其思想是讲区间[a，b]平分成m段，在每段上使用Newton-Cotes算法，最后将各段结果求即为积分的近似值。

【定理1】[1]n阶Newton-Cotes算法的离散误差

为

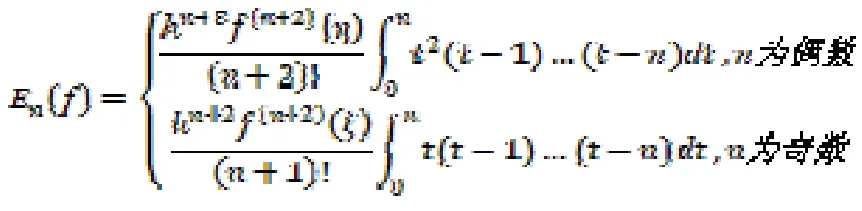
由此当n较大时离散误差会发散。

但是实际数值计算试验中并没有表现出上述定理所述的结果，这是因为上述定理认为Ai的计算是绝对准确的，但实际计算中只是还是使用数值积分方法计算该Ai，只是计算多项式积分的计算更准确一点。然而这却导致了在n上升到较小值的之后误差就不再明显下降。于是我们提出了如下算法。

3 后置秦氏复合Newton-Cotes算法

在经典的复合Newton-Cotes算法中我们会使用，秦九韶算法计算多项式的值之后再进行数值积分。我们这里观察发现其实Ai的计算可以利用多项式积分的特点进行优化。在后置秦氏复合Newton-Cotes算法中我们先计算出Ai中多项式的系数，之后对系数矩阵做加权平移就可以得到积分后多项式的系数矩阵，然后再使用秦九韶算法计算Ai。这相当于将秦氏算法后置，所以我们取名为后置秦氏复合Newton-Cotes算法。具体介绍之前我们先引入一个引理。

【引理1】k次多项式Pk(t)的系数矩阵为

下图表示了后置秦氏复合Newton-Cotes算法的图示。

4 算例与分析

我们将分别使用经典的复合Newton-Cotes算法和后置秦氏复合Newton-Cotes算法计算计算积分，并对比计算结果。

【试验一】：使用经典的复合Newton-Cotes算法（m是分段数，n表示Newton-Cotes算法的阶数）

下图中上方曲线是m=100时误差随n变化的曲线，下方是m=10000时的曲线。纵坐标是对数坐标表示误差的绝对值。

实验表明经典算法在n在3和8之间精度没有明显增长，并验证了定理一中的关于数值不稳定的结论。

【实验二】：使用后置秦氏复合Newton-Cotes算法

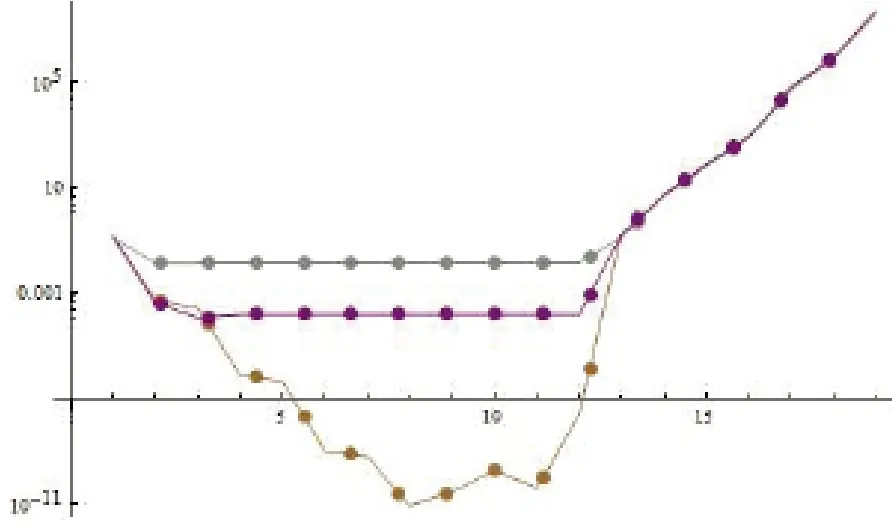
上图中上方两条是实验一中的数据。最下方曲线是m=10000时候误差随n上升变化的曲线。

实验表明使用改进之后的后置秦氏复合Newton-Cotes算法可以明显地增强算法的精度。

【实验三】：对比上述试验中计算出的Newton-Cotes系数Ai

参考[2]中给定的Cotes系数，我们发现经典算法的系数对称性和精确度都没有改进算法好，我们分析认为这正是新算法精度较高的原因。

5 结论

使用我们设计的后置秦氏复合Newton-Cotes算法在不明显增加计算量的情况下可以大大增加计算结果的精度，尤其在Cotes系数的对称性上有比较大的改进。

参考文献

[1]林成森.《数值计算方法.上册》.科学出版社.

[2]黄云清.《数值计算方法》.科学出版社.