基于粒子群算法的直线感应电机优化设计

喻 晓， 林荣文， 吴冠平

(福州大学电气工程与自动化学院，福建福州 350108)

0 引言

直线电机是一种将电能直接转换为直线运动机械能的电力传动装置。在实现直线运动的功能上，由于直线电机不需要任何转换装置而直接产生推力，与传动的旋转电机相比有着优越的实用性和便捷性，常被运用于轨道交通和升降电梯等领域。但由于其特有的端部效应，直线电机的效率和功率因数比同容量的旋转电机低，尤其在低速时比较明显。

粒子群优化算法(Particle Swarm Optimization Algorithm，PSO)是一种基于群体智能的进化计算方法，基本概念源于对鸟群捕食行为的研究。PSO的搜索过程是从问题解的一个集合开始，而不是从单个个体开始，具有隐含并行搜索特性，减小了陷入局部极小的可能性。PSO有记忆，好的解的知识粒子都保存，每个粒子在算法结束时仍然保持着其个体极值。由于PSO不受函数约束条件的限制，但直线感应电机的优化问题属于有约束条件的非线性规划问题，故本文将约束条件转化为惩罚因子加入原目标函数，转化为无约束极值问题。同时，引入线性递减的惯性权重来平衡全局搜索能力和局部搜索能力。试验表明，PSO在满足约束条件的情况下，可以较好地实现以提高功率因素和同步效率为目的的直线感应电机结构参数优化。

1 直线感应电机基本原理

1．1 工作原理

直线电机的种类有很多，本文的研究对象是中低速磁悬浮列车中常用到的单边短初级直线感应电机(Linear Induction Motor，LIM)。其工作原理与旋转感应电机类似，只是将旋转电机在顶上沿径向剖开，把圆周拉直。在LIM的三相绕组中通入三相对称正弦电流，产生沿展开方向成正弦分布的气隙磁场。当三相电流随时间变化，气隙磁场将平行移动，称之为行波磁场。次级线圈在行波磁场的切割下将产生感应电动势并感应电流，而电流和气隙磁场相互作用便产生电磁推力，推动初级沿着行波磁场的方向运动。这就是LIM的基本工作原理。

旋转电机的气隙是闭合的圆周，而直线电机的气隙是一条直线，有入口和出口，这会导致三相绕组彼此的互感不相等，从而产生反向磁场和脉振磁场，增加阻力和附加损耗，该现象被称为纵向端部效应，是直线电机设计与优化过程中不得不考虑的因素。

1．2 电磁计算

对于钢次级的LIM，既要考虑次级导体板导磁性能的非线性，又要考虑直线电机所特有的边端效应，因此其电磁计算是个相当复杂的问题［4］。实践证明，采用实心转子异步电机常用的磁阻抗法来计算直线电机的励磁阻抗和次级钢板的等效阻抗，并在此基础上引入等效电阻Red来近似考虑纵向边缘效应的影响，此方法在工程上是可行的。

考虑纵向边端效应的钢次级LIM等效电路如图1所示。

图1 考虑纵向边端效应的等效电路

LIM的参数计算公式如下。

初级绕组每相电阻:

励磁电抗:

初级绕组漏抗:

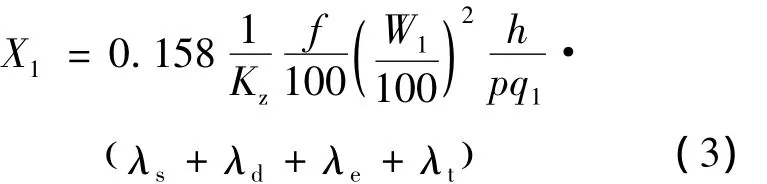
纵向边端效应等效电阻:

其中:

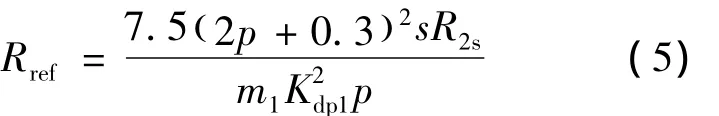
等效电磁电阻:

等效电磁电抗:

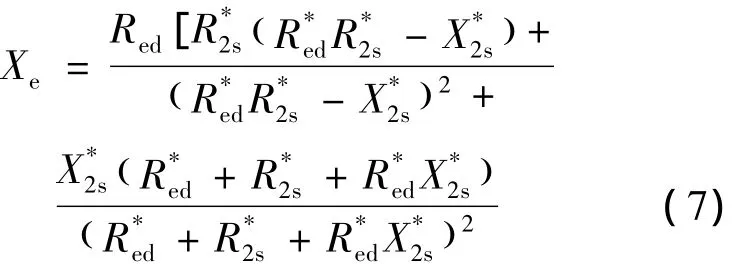
式中:——初级绕组每相串联匝数;

lc——线圈平均半匝长度;

ρ——初级电阻率;

a1——并联路数;

s——转差率;

μ0——真空的磁导率;

f——频率;

τ——极距;

h——初级叠片厚度;

m1——相数;

W1——初级绕组每相串联匝数;

kdp1——绕组系数;

δ——气隙大小;

KδKμ——气隙系数和饱和系数乘积;

p——极对数;

Kz——每槽导体系数;

q1——初级每极每相槽数;

λs+λd+λe+λt——漏磁导系数之和;

R2s——次级归算等效电阻;

直线感应电机的起动性能计算如下。

起动电流:

功率因数:

起动推力:

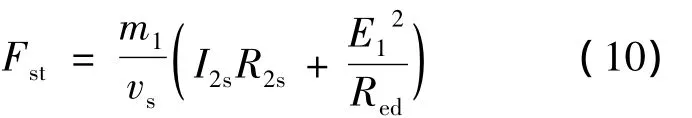
起动同步功率:

起动时输入功率:

同步效率:

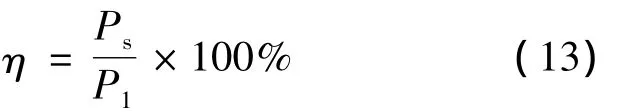
式中:U1——初级相电压;

vs——同步速;

I2s——次级归算电流;

E1——感应电动势。

2 PSO基本原理

在PSO中，把一个优化问题看作是在空中觅食的鸟群，“食物”就是优化问题的最优解，而在空中飞行的每一只觅食的“鸟”就是PSO算法中在解空间中进行搜索的一个粒子。粒子在搜索空间中以一定的速度飞行，该速度根据其本身的飞行经验和同伴的飞行经验来动态调整。所有的粒子都有一个被目标函数决定的适应值，该适应值用于评价粒子的“好坏”程度。

每个粒子知道自己到目前为止发现的最好位置(Pbest)和当前的位置，Pbest就是粒子本身找到的最优解，这个可看作是粒子自己的飞行经验。除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(Gbest)，Gbest是在Pbest中的最好值，即是全局最优解，这个可看作是整个群体的经验。用随机解初始化一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪个体极值(Pbest)和全局极值(Gbest)来更新自己。找到这两个最好解后，接下来是PSO中最重要的“加速”过程，每个粒子不断改变其在解空间中的速度，以尽可能地朝Pbest和Gbest所指向的区域“飞”去。

一般数学模型如下:

假设在一个N维空间进行搜索，粒子i的信息可用两个N维向量来表示:

粒子位置表示为x= (x，x，…x)Tii1i2iN

速度为v= (v，v，…v)Tii1i2iN

在找到两个最优解后，粒子即可根据式(14)、式(15)来更新自己的速度和位置:

式中:vkid——粒子i在第k次迭代中第d维的速度;

xk——粒子i在第k次迭代中第d维的位

id置;

i——种群大小，i=1，2，3…M;

c1、c2——学习因子，或称加速系数，合适的c1和c2既可加快收敛又不易陷入局部最优;

rand1、rand2——介于［0，1］之间的随机数;

Pbestkid——粒子i在第d维的个体极值点的位置;

Gbestkd——整个种群在第d维的全局极值点的位置。

在粒子群算法中，为解决速度快、精度低、易发散等缺点，通常引入惯性权重w-，则式(14)改进为

3 LIM优化设计的实现

3．1 目标函数的选取

本文是针对LIM功率因数和同步效率低于同容量的旋转电机而进行的优化设计，所以选取的优化目标是功率因数和同步效率。多目标优化的常见处理方法是把各个目标函数统一到一个目标函数里面。在此，将功率因数和同步效率相乘，并用1减去该乘积，将求极大值问题转化为求极小值问题，初步目标函数如下:

3．2 约束条件的选取

综合考虑LIM的性能指标和生产成本，本文选取同步效率、功率因数、起动推力和起动电流作为优化的约束条件。为了使各约束函数值达到相同数量级，使用相对值的形式，表达式如式(18)所示:

PSO属于无约束优化算法，本身不能处理约束条件。因此要对约束条件进行转化，构成无约束的增广目标函数。引入惩罚函数:

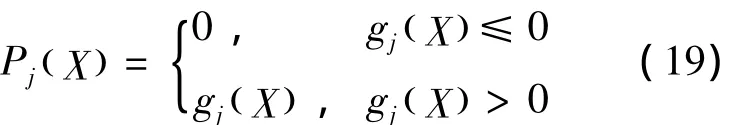
3．3 优化变量的选取

通常设计变量的选择原则是:一般选取对电机性能影响大，对目标函数和约束条件影响大，且能相应确定其他有关参量的独立设计变量为优化设计变量。本文根据LIM特点及性能要求取优化变量为初级叠片厚度h、初级槽深ds、初级槽宽b1、槽口宽b0和气隙大小δ。表达式如下:

当满足约束条件时，惩罚函数不发挥作用;当不满足约束条件时，惩罚函数按照一定的权值ωj附加在目标函数中，寻优时便纳入考虑。改进后的目标函数(增广目标函数)如下:

3．4 优化程序设计

在前文对LIM电磁性能计算方法以及PSO实现方法研究的基础上，采用MATLAB软件进行编程运算。程序模块包括电磁计算模块、粒子群初始化模块、粒子更新模块和寻优主模块。程序流程如图2所示。

3．5 优化结果

初始输入数据如表1所示。

电磁计算模块编程时，式(1)～式(7)中未知参数的算法或取值，参考文献［5］可得。

优化结果输出如表2所示。

最佳适应度曲线如图3所示。

4 试验结果分析

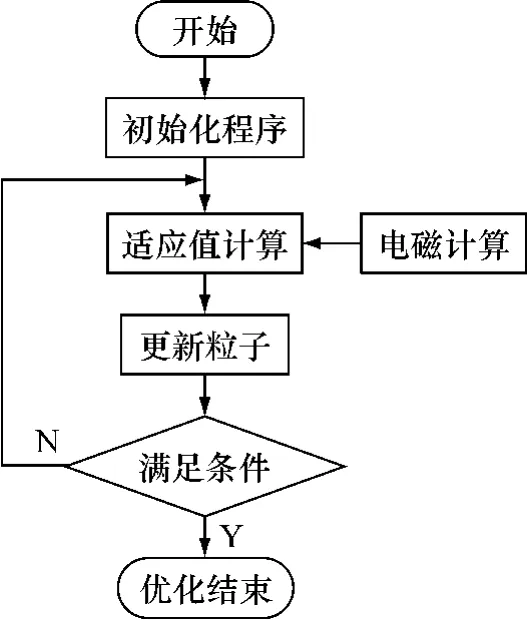
图2 程序流程图

表1 初始数据输入表

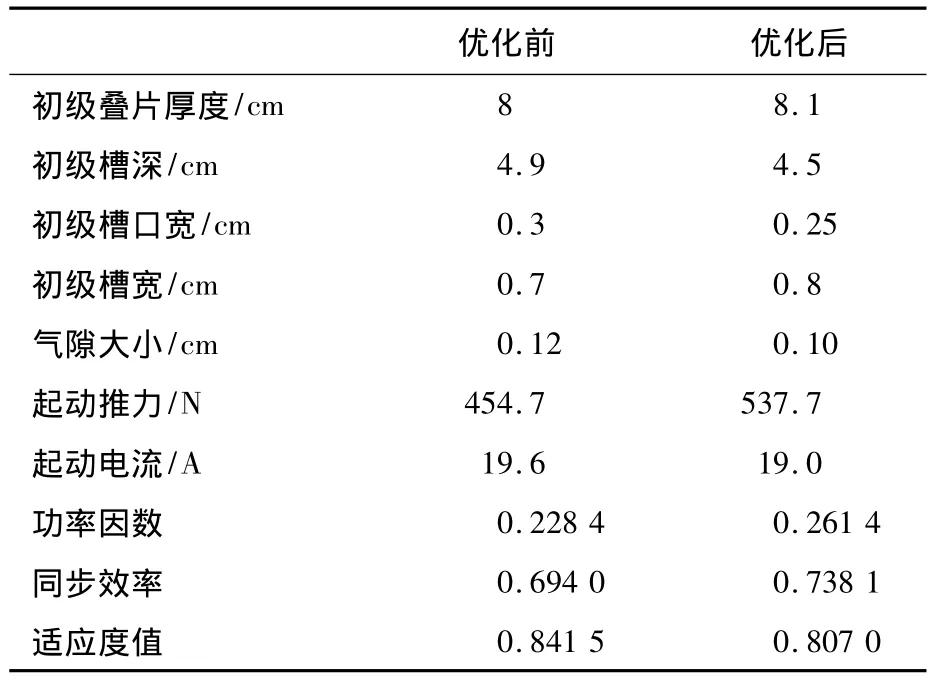
表2 优化结果输出

图3 最佳适应度曲线

试验结果显示:经PSO优化运算后，在设计允许范围内，初级叠片厚度、初级槽宽的大小略有增加，而初级槽深、初级槽口宽和气隙大小的取值略有减小;功率因数较优化前提高14.4%，同步效率较优化前提高6.4%，适应度值减少4.1%，同时还实现起动推力较优化前提高18.2%，起动电流较优化前减少3.1%;最佳适应度曲线显示算法收敛，说明计算是正确的。

5 结语

本文通过理论阐述及试验运算，得出结论如下:PSO以其原理简单、容易编程实现、不易发散的优点，适用于LIM优化设计。但是，PSO也存在收敛快的特点，需要不断调整惯性权重和最大飞行速度的值来避免优化陷入局部最优。

［1］叶云岳.直线电机原理与应用［M］.北京:机械工业出版社，2000.

［2］焦留成，朱建铭.直线感应电动机结构参数对功率因数及效率的影响研究［J］.焦作矿业学院学报，1995(6):71-77.

［3］郭亮，卢琴芬，叶云岳.基于粒子群算法的直线振动发电机优化设计［J］.电机与控制学报，2008(4):442-446.

［4］傅丰礼，唐孝镐.异步电动机设计手册［M］.北京:机械工业出版社，2002.

［5］张小玲.粒子群算法在圆筒型直线感应电机优化设计中的应用［D］.沈阳:沈阳工业大学，2010.

［6］张贤明.MATLAB语言及应用案例［M］.南京:东南大学出版社，2010.

［7］Jeong Hyoun Sung，Kwanghee Nam.A new approach to vector control for a linear induction motor considering end effects［C］∥Thirty-Fourth IAS Annual Meeting，Conference Record of the 1999 IEEE，1999(4):2284-2289.