全埋式抗滑桩合理桩长研究

刘军武

0 引言

自然界中存在着大量的滑坡，坡体的滑动给人类带来了巨大损失。滑坡治理是岩土工程的主要任务之一，从20世纪30年代开始，抗滑桩便成为重要的支挡结构形式，在铁路、公路、厂矿等滑坡中有着广泛的应用[1］。

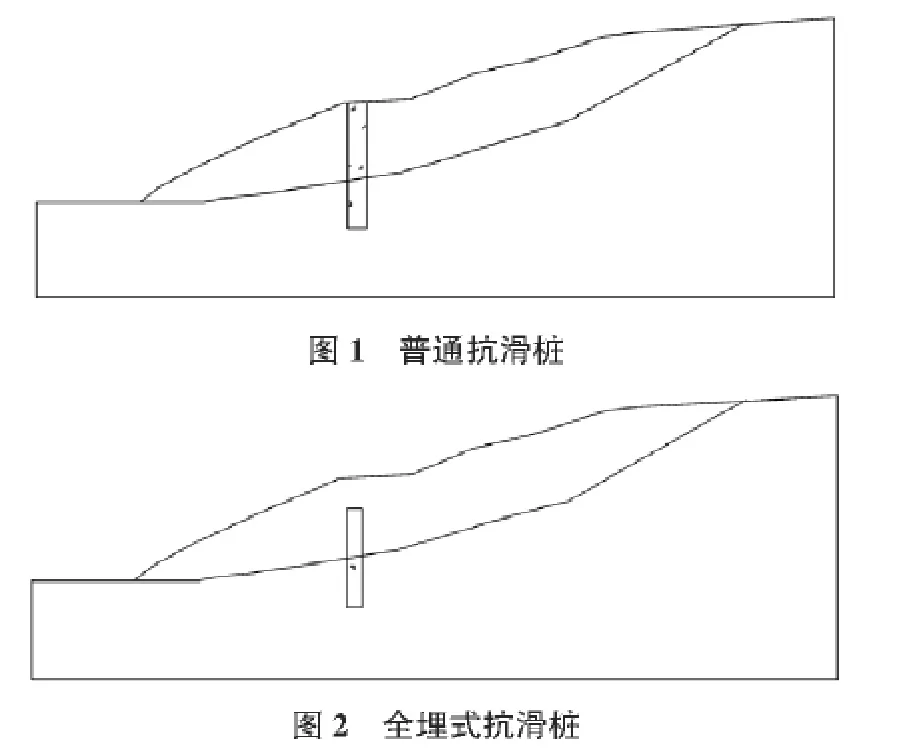
根据抗滑桩桩顶是否到达滑坡体地表可将抗滑桩分为普通抗滑桩和全埋式抗滑桩(见图1，图2)，全埋式抗滑桩的桩顶距滑坡体表面有一定距离，桩顶上的部分推力转移到滑体上，充分的利用了滑坡体的自身抗力，相对于普通抗滑桩不仅桩长减短，而且其弯矩、剪力也减小，更经济合理[2］。目前，对普通抗滑桩的研究较多，而对全埋式抗滑桩研究较少。文献[3］利用模型试验对桩体受力分布形式和规律进行了研究;文献[4］利用模型试验对全埋式抗滑桩的桩前和桩后坡体受力状态及桩长变化时坡体破坏形式等进行了研究。

全埋式抗滑桩的关键问题是桩长的确定，当桩长较短桩顶距离坡体表面较深时，滑坡容易产生越顶破坏;当距离较浅时，则桩体弯矩较大，材料用量较多造成浪费。本文在有限元的基础上，利用强度折减法分析研究全埋式抗滑桩合理的嵌固长度及自由段长度。

1 分析方法

研究滑坡稳定性的方法很多，如条分法、斯宾塞法、传递系数法等都是基于极限平衡理论，其优点可以直接的给出边坡或者滑坡的安全系数，概念明确便于工程应用，其缺点也非常明显，由于假设土体为刚塑体，不能计算出土体的变形及土体内部的应力分布，特别是有支挡结构时，不能得出支挡结构的内力及其位移。有限单元法不仅考虑了力的平衡条件，还考虑了土体的本构关系，可以考虑土体的非线性、复杂边界条件等。同时，在有限元中使用强度折减法不仅可以计算出应力和位移分布，还可以得出安全系数。

由Zienkiewicz提出强度折减法，其原理是将土体参数强度c，φ同时除以一个折减系数Fr折减后的土体强度参数为:

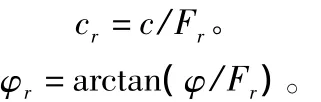
其中，cr，φr均为折减后的土体强度参数。

计算时，假设不同的强度折减系数，根据折减后的土体参数进行有限元分析，当达到临界破坏时的强度折减系数就是边坡的稳定性安全系数Fs。判断土体到达临界破坏状态的标准有多种，本文采用土体是否产生的连续的贯通区作为判断标准。

2 计算模型

本文以陕西南部某一滑坡为研究对象，将滑坡简化为平面应变问题，建立二维有限元模型，模型单元划分如图3所示。

滑坡体的土层采用摩尔—库仑本构模型，各层岩土参数见表1。

表1 计算参数

布置抗滑桩处的滑坡体厚度为12 m，抗滑桩间距4 m，对抗滑桩不同自由段长度和嵌固段长度进行计算分析，以便得出全埋式抗滑桩合理桩长。

3 合理桩长

全埋式抗滑桩的桩长包括两个部分:滑裂面上的自由段长度和滑裂面下的嵌固端长度。为了研究其合理的长度，本文分别对自由段长度和嵌固端长度进行研究。

3.1 自由段长度

为了确定全埋式抗滑桩安全经济的自由段长度，需对设置了不同自由段长度的全埋式抗滑桩边坡进行计算，得出不同情况下边坡的安全系数。

图4，图5给出了嵌固端为6 m和8 m时，不同自由段长度对滑坡安全系数的影响。

从图4，图5中可以看出，在不同的嵌固端下，安全系数都随着自由段长度的增加而增加。但当自由段大于8 m时，滑坡的安全系数趋于稳定，增加不明显，说明增加自由段的长度对安全系数影响不大。当自由段大于3 m时，即当自由段大于滑体厚度的1/4时，加固后的边坡安全系数均大于1.25，边坡稳定，满足滑坡的治理要求。

3.2 嵌固端长度

为了分析确定合理的嵌固端长度，本文计算了一系列自由段长度下，不同嵌固端长度对滑坡安全系数的影响。图6仅给出了自由段长度为5 m时，不同嵌固端长度对安全系数的影响。其余的规律与之相似。

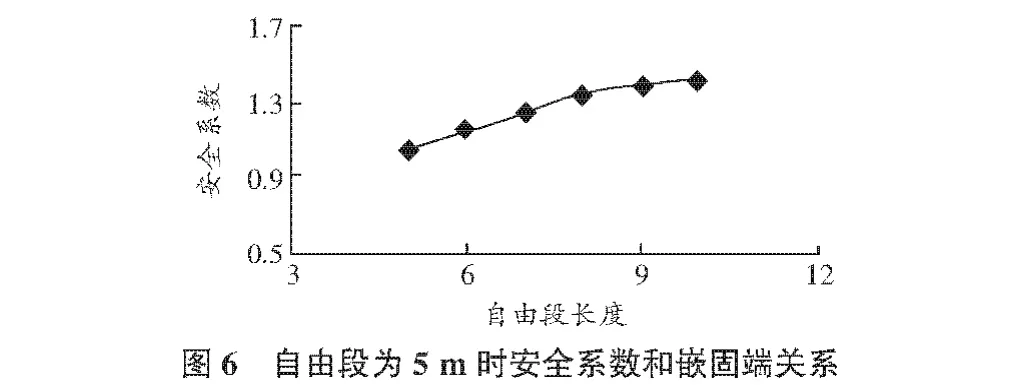
从图6中可以看出，当自由段长度一定时，滑坡的安全系数随着嵌固端长度的增加而增加，到达7 m后，安全系数增加较小，说明嵌固端大于一定长度后，对滑坡的安全系数影响较小。嵌固端长度大于6 m，滑坡的安全系数大于1.25，说明嵌固端大于滑体厚度1/2，满足滑坡的治理要求。

4 结语

通过计算分析，可以得出如下结论:

1)相较于传统的普通抗滑桩，全埋式抗滑桩桩长较短，受力更为合理，花费更为经济;

2)滑坡的安全系数随着全埋式抗滑桩自由段长度和嵌固端长度增加而增加，当大于一定长度后安全系数变化不大;

3)全埋式抗滑桩自由段长度不宜小于所在位置的滑坡体厚度的1/4;

4)全埋式抗滑桩嵌固端长度不宜小于所在位置的滑坡体厚度的1/2。

[1]李海光.新型支挡结构设计与工程实例[M］.北京:人民交通出版社，2004.

[2]雷 用，赵尚毅.支挡结构设计与施工[M］.北京:中国建筑工业出版社，2009.

[3]熊治文.深埋式抗滑桩的受力分布规律[J］.中国铁道科学，2000，21(1):48-56.

[4]雷文杰，郑颖人，王恭先.沉埋桩加固滑坡体模型试验的机制分析[J］.岩石力学与工程学报，2002，102(6):5-11.

[5]熊治文，马 辉，朱海东.全埋式双排抗滑桩的受力分布[J］.路基工程，2002，26(7):1347-1351.