梯形磁密作用下同步发电机相电势分析*
饶 翔,吴旭升,任明炜,高 嵬
(1.海军工程大学电气与信息工程学院,武汉 430033;2.江苏大学电气与信息工程学院,镇江 212013)
带整流负载的同步发电机空载运行时相电势的波形与传统的正弦波形有很大差异,为保证更好地整流换向,相电势的波形一般为等腰梯形。其中包括上边宽度为120°或接近120°的梯形相电势波形(图1a)。此时斜边的形状具有很大任意性。如果对相电势的正弦性不作要求的话则扁平形状的相电势波形更符合要求,在相同的磁路下,扁平磁场下实际的感应强度比正弦情况下低很多,或者说在相同的磁饱和情况下扁平磁场有效体积利用率更高。专门为带整流负载而特别设计的同步发电机其质量及外观尺寸等指标均优于普通工业用途的发电机。普通工业用途的同步发电机因为气隙中磁感应强度B的形状使得发电机相感应电势接近正弦形[1~3]。在不考虑定子齿谐波对相电势的影响时,由于绕组采用短距分布,使得高次谐波绕组系数较基波小,因而使高次谐波被全部或部分削弱[4]。
传统对相电势分析方法是将磁感应强度分解为一系列谐波并借助于绕组系数确定相电势中谐波成分[5,6]。至于相电势的合成问题则采用相反的步骤,即通过将谐波相电势求和的方法求得合成相电势。在梯形磁场中一个周期内谐波的和是有限的,为了考察所求的和是否足够大,以保证误差在(0.5~1)% 范围内,所需计算的谐波数必须足够大以便获得满意的结果。显然这种方法是精确的,机械的,缺乏直观性。在梯形磁场中根据相电势的定义,不采用磁场和电势的谐波分析法,也可求得合成相电势并对其特点进行分析。
1 整距绕组相电势波形分析
图1所示为同步发电机仅带整流负载时理想相电势和磁密波形。
假设每极每相槽数为q、短距系数为β,按空间磁密实际形状来确定感应电势波形。气隙中一根单位导体运动电势瞬时值为

式中,V为磁感应强度B1点的导体线速度。
分布在不同磁感应强度点 B1,B2,B3,… 的几根串联导体的电势为

上式结果的符号由磁感应强度的极性和绕组连接方式确定。
感应电势的形状由气隙中磁场的形状决定。不考虑饱和时,对于气隙均匀、转子表面绕线为γ(γ是转子每极下嵌放绕组部分与极距之比):

隐极式电机和极弧长度近似为bp=0.75的凸极电机具有接近梯形分布的磁感应强度。由e1的表达式可知,理想情况下一根导体(或相对跨距为β=1的一个线圈)的电势形状重复着空间磁感应强度的分布。然而对于实际的电机这将对应于每极每相槽数q=1的定子绕组,由于参数特点和设计方面的原因,这是不可接受的,更主要的是此时齿谐波γz的次数较低。

对于带整流负载工作常采用的六相十二个相带绕组来说q=2是可以接受的,因为此时齿谐波γz的次数为23和25,这与q=4的三相绕组的齿谐波的情况相同[7]。当相带宽为α3=时,一相相邻两线圈的角度为

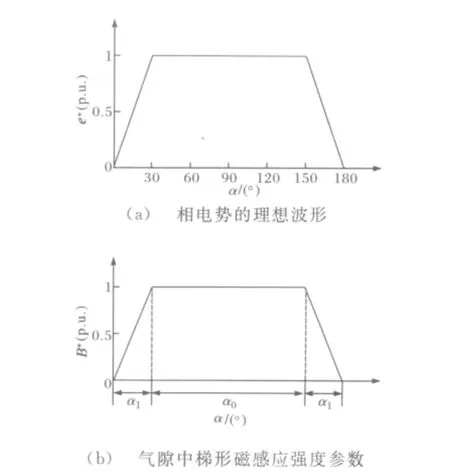
图1 同步发电机仅带整流负载时理想相电势和磁密波形Fig.1 Ideals potential and flux density waveform of synchronous generator only with the rectifier load
在图2中画出了相对节距β=1的两个线圈(即整距线圈)感应电势及它们的和。假设每个线圈的感应电势为1,则叠加后两个线圈产生的电势和为e'=e1+e2=2(等于线圈数)。为了后面分析方便及作图清晰起见,将电势和e'除以2(即线圈数)这样电势和变为e=e1+e2=1,如图中粗实线所示。可见(αu1,eu1)是转折点。显然,该周期性的图像继续往下画是一样的。
由此可见,合成感应电势曲线在αu1发生转折。对于两个线圈的合成感应电势来说其特点是,由于侧边出现折点其梯形图形出现“失真”,同初始磁密图形比较其上边宽度α减小。
并且

侧边转折点位于

折点处感应电势值为

对于六相绕组来讲,对应于某个磁极磁密宽度α0时折点处感应电势EMF值如表1所示。
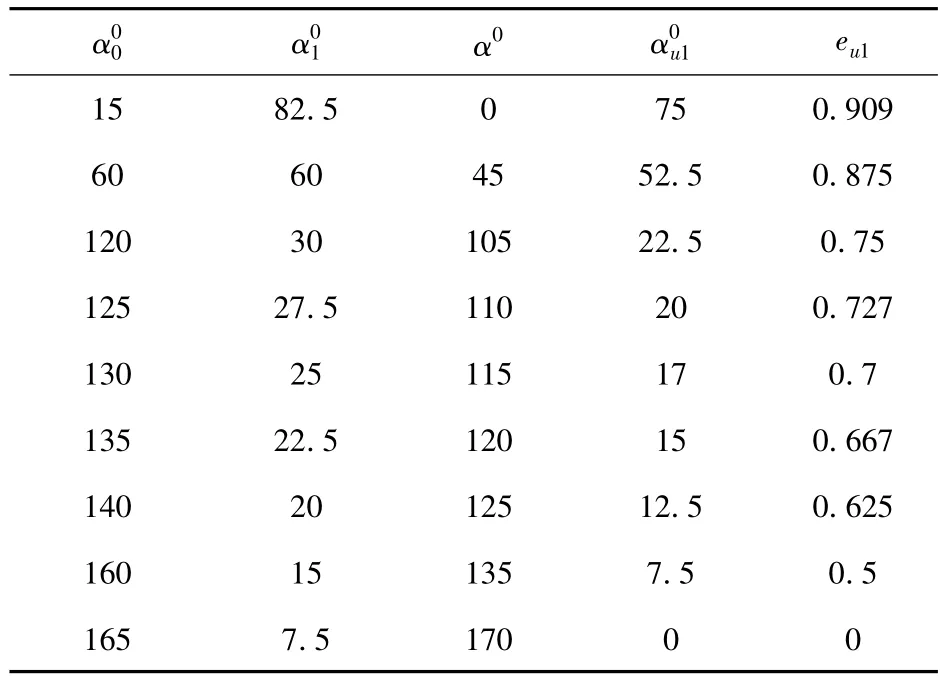
表1 m=6,q=2,αq=15°,β =1 时感应电势值Tab.1 Electromotive force value as m=6,q=2,αq=15°,β =1
表中示出了参数值的极限情况。当α0=αq=15°时,侧边带折点的梯形过渡为侧边带折点(αu1=75°) 的三角形(α =0);当 α0=165°(α1=)时,侧边带折点的梯形过渡为正常的等腰梯形(αu1=0)。标出极限过渡情况在理论上有重要意义。对极弧长度接近bp=0.75的凸极电机或γ=0.25的绕线转子隐极电机来说,α0工作区间通常在60°~ 135°。当磁密的宽度α0=135°时,可以使合成感应电势上边的宽度为α=120°。
当q>2时,感应电势和的求法类似。图3a、3b中示出了q=3,4时的感应电势和。
相邻两线圈之间的角度分别为

由图可见,感应电势波形上边比q=2时的小,因为随着q的增大,在一相范围内线圈边之间的角度也增大,侧边上的折点数增加为(q-1)个。q的提高会使感应电势的波形和原始磁密波形相比失真较大。
在极端情况下,当q=∞时侧边在点(αu1,eu1)处以圆弧的形式连接成一点。当q=∞,αq角等于相带宽度αph时,感应电势和的上边将缩短。即

在极弧宽度α0大于相带宽度αph时,在感应电势曲线上出现平坦部分。

图3 三整距和四整距线圈感应电势波形Fig.3 Induced voltage waveform of three and four full coils
随着α0减少该部分减少(图4a和图5)。在α0=αph点处平坦部分消失α=0,感应电势曲线最接近正弦形(图4a曲线1);随着α0进一步减小α0<αph,在感应电势曲线上又出现平坦部分α,此时感应电势的幅值将小于1(图4b)。
理论上,在极限情况下当磁通为三角形时α0=0,α有最大值α=αph,感应电势的幅值达到最小值e=0.667。因此,磁密波形为梯形的情况下,上边宽度α0=αph时,可保证相电势的波形最接近正弦形。
对于六相绕组来说,最佳值为α0=30°,因此有 γ =0.833,bp=0.166。对于三相绕组最佳值为α0=60°,γ =0.667,bp=0.333。对于隐极电机上述理论分析得到的γ值是可以接受的,对于凸极电机上述 bp值不采用[8]。

图4 三相绕组相电势波形Fig.4 Phase voltage waveform of three-phase winding

图5 当 m=6,q= ∞,αph=30°,β=1时,六相绕组相电势波形Fig.5 phase voltage waveform of six-phase windings under m=6,q= ∞,αph=30°,β =1
2 短距绕组电势波形分析
下面研究梯形磁密下感应电势波形中的短距现象,见图6。
首先研究q=1,β<1的情况。在研究整距绕组时相距第一条边为π的线圈的第二条边可以不考虑,但在研究短距情况时两条边都必须考虑,因为两条边间的距离为βπ。
考虑短距时对电势最直接的影响就是波形变化。当相带数为2m时第二个线圈对称的位于第二个磁极下,在整距情况下该线圈是不考虑的。当存在短距时应当一起研究两个线圈,见图6(a)。
第一个线圈的两条边用1-1'标识,第二个线圈的两条边用2-2'标识,仿照电机设计中常规的分析方法将两个短距线圈用两个等效的整距线圈来代替,等效整距线圈的两条边为1-2',2-1'。
因此,实际短距线圈的电势波形可由前面研究的q'=2的整距线圈来等效。等效线圈相邻两条边的角度由短距系数β确定,即

在定子开槽的情况下,短距系数β可以采用离散值:

这里 k=1,2,3…,因此 αβ等于

按照上述思想,当k=1时,有αβ=αq,q=1的实际短距绕组等效转化为q'=2的整距绕组来分析(见表2)。这个规律可以扩展到一般情况即q>1,β<1的绕组。
因此,短距绕组感应电势波形确定问题可以归结为等效线圈数为q'=2q的整距分布线圈的感应电势问题,此时等效线圈相互位置由q和β确定,因此短距将导致感应电势波形和磁密波形相比进一步失真。以q=2和k=1,2,3的情况来加以说明,见图6(b)。
为削弱电枢反应磁势11和13次空间谐波,对六相绕组,当k=1推荐β=0.916。等效线圈之间的角度αβ=αq=15°与实际角度αq相等,因此等效线圈的一部分安放在实际线圈上。边的安放如图6b所示(β =0.916,k1=1)。这时感应电势的上边是α =α0-30°而不是q=3,β=1时的α =α0-20°。若 k=2,则 β =0.833,αβ=2αq=30°,等效线圈边的分布如图6b所示(β =0.833,k2=2),此时上边的宽度为α=α0-45°而不是q=4,β=1时的 α = α0- 22.5°。
进一步增大到k=3,β=0.75,四个等效线圈构成两个线圈组,每个线圈组两个线圈见(图6b,β=0.75,k3=3)。

图6 短距线圈的等效分布Fig.6 Equivalent distribution of short-range coil

表2 β=1时不同q值对应的感应电势参数Tab.2 Parameters of induced voltage at different q values when β =1
3 正弦形感应电势波形参数选取
最后研究一下q及β值较大时的绕组情况,显然,这些绕组不能给出上边为足够宽的梯形波感应电势。这里将正弦形感应电势波形的优化作为例子。
研究q=∞,β<1的绕组,类似上述短距绕组研究方法,问题归结为研究等效区间宽度为,β=1,q=∞ 的等效绕组由实际宽度αph和β来确定:

前面已提及的六相绕组可以有两个短距系数β =0.833,β =0.916。
当β=0.833时等效宽度是α=60°,该六相绕组的相感应电势波形与β=1的三相绕组相同(图4a、b)。此时若要求感应电势为正弦形,理论上讲,最优值为 α0==60°,相应地 γ =0.667,bp=0.333。
对于三相绕组,研究短距为β=0.667和β=0.833。在第一种短距下等效宽度为=120°,在第二种短距下等效宽度为=90°,此时理论上最优参数为 α0=90°,相应地 γ =0.333,0.500,bp=0.667,0.500。
由此可见考虑到γ值的实际选取,六相汽轮发电机较三相汽轮发电机更接近最优值[8]。
4 结语
(1)对于整距绕组情况,随着每极每相槽数q的增大会使感应电势的波形和原磁密波形相比失真较大,在极端情况下,当q=∞时,相电势梯形波的两侧边变为圆弧形式,当极弧宽度等于相带宽度时,可得到最接近正弦形的相电势。
(2)对于短距绕组,由于实际的每极每相槽数为q的短距绕组可以归结为等效的每极每相槽数为q'=2q的整距绕组,因此短距将导致感应电势波形和磁密波形相比进一步失真。
(3)上述分析只用于分析磁密波形为梯形的情况。对于常用的工业用同步发电机,在实践上采用熟知的方法可以获得很好的接近正弦波形的磁密波形。但在显著剔除了磁场中正弦波的情况下,可以采用上述分析方法,例如在考虑转子磁势的阶梯形时,在考虑磁饱和程度很高时等等。
[1]Franklin Paul W.Theoretical study of the three phase salient pole type generator with simultaneous AC and bridge rectified DC output[J].IEEE Trans on Power Apparatus and Systems,1973,92(2):543 -557.
[2]杨建华,高军(Yang Jianhua,Gao Jun).考虑磁饱和影响的同步发电机励磁电流计算(Field current calculation of synchronous generators taking into account the magnetic saturation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(2):104 -108.
[3]谢莉,雷银照(Xie Li,Lei Yinzhao).同步发电机整流系统的时域模型与瞬态计算(Time domain model and transient calculation of synchronous generator rectifier system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(1):26 -30.
[4]许实章.交流电机的绕组理论[M].北京:机械工业出版社,1985.
[5]许善椿,金波,李春廷,等(Xu Shanchun,Jin Bo,Li Chunting,et al).交流电机定子分数槽绕组的谐波磁势问题(Harmonic magneto-motive of fractional-slot sta-tor winding or ac electric machines)[J].大电机技术(Large Electric Machine and Hydraulic Turbine),1999,18(3):1 -5.
[6]陈乔夫(Chen Qiaofu).正规大小相带分数槽绕组的谐波分析(Analysis of harmonic magneto-motive of normal size fractional-slot winding)[J].中小型电机(E-lectric Machines and Control Application),1989,16(5):5-7.
[7]饶翔,吴旭升,任明炜,等(Rao Xiang,Wu Xusheng,Ren Mingwei,et al).不对称六相分数槽绕组磁势分析(Analysis of armature magnetometive force on anisomerous hex-phase fraction slot winding)[J].大电机技术(Large Electric Machine and Hydraulic Turbine),2011,216(3):21 -27.
[8]陈世坤.电机设计[M].北京:机械工业出版社,2000.

