基于微粒群区域搜索和小波评价的差分式自动聚焦

吕恒毅，刘 杨，薛旭成

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.哈尔滨工业大学控制科学与工程系，黑龙江哈尔滨150001）

基于微粒群区域搜索和小波评价的差分式自动聚焦

吕恒毅1，刘 杨2，薛旭成1

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.哈尔滨工业大学控制科学与工程系，黑龙江哈尔滨150001）

为进一步提高图像法自动聚焦的性能，提出了一种差分式提取图像边缘的方法，并构造了图像清晰度的小波评价函数，同时利用微粒群（PSO）算法对聚焦区域进行快速搜索。首先，介绍了差分式边缘提取方法及其优势，给出了一种评价区域的选取判据以及基于PSO的高效搜索方法；然后，对小波评价函数参数进行了比较分析和优选；最后，与传统方法进行了对比实验。结果表明，由于采用了差分式提取方法以及新的自适应聚焦窗口和评价函数，聚焦曲线较传统方法具有更高的调焦分辨率，PSO算法的使用使聚焦速度提高了约170 ms，聚焦精度约为2.3 μm，同时调焦效果不受初始位置的影响。

自动聚焦；差分式边缘提取；聚焦区域选择；微粒群（PSO）算法；清晰度评价函数；小波变换

1 引 言

自动聚焦［1～3］是获取高分辨率图像的关键技术，它在数字成像系统、计算机视觉和视频监控等领域起着至关重要的作用。自动聚焦通常包括3个步骤：聚焦区域的选择［4］、评价函数的计算和聚焦位置搜索算法。聚焦区域选择能够有效提高聚焦效率，同时获取对评价函数相对有利的评价窗口，但传统的聚焦区域搜索算法耗时较大，且搜索到的聚焦区域内的图像仍会包含一部分低频冗余信息，对评价函数灵敏度和稳定性十分不利；评价函数是自动聚焦中的核心部分，决定了图像法自动聚焦［5］的精度和速度，国内外学者对此进行了深入的研究，并提出了众多的评价函数形式［6～10］，但传统曲线形态大多存在着有效调焦范围过窄或聚焦位置附近灵敏度不高的不足。鉴于此，本文提出了差分式提取图像边缘的方法来剔除低频冗余，并为之匹配设计了小波评价函数和基于微粒群算法（PSO）的评价区域搜索方法，得到了优于传统方法的结果。

2 图像边缘的差分式提取

图像中的低频成份不仅严重影响评价函数曲线的灵敏度，而且可能影响评价函数的判断正确性［9］。对于一幅清晰的图像，在离焦过程中，锐度大的边缘信息衰减相对较慢，在离焦量较大时仍能辨认出其基本的轮廓信息，而锐度较小的边缘信息则消失殆尽；在聚焦过程中，图像的高频成分逐渐变得清晰，而低频成分变化不明显。因此，将调焦过程中每步的图像与初始离焦图像做差并求绝对值，便可得到低频含量很小的图像边缘分量，并作为评价函数计算的输入图像，其表达式如式（1）所示。

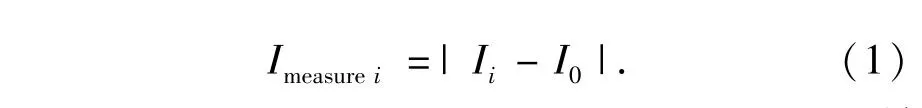
传统方法以原始图像作为输入，如式（2）所示。

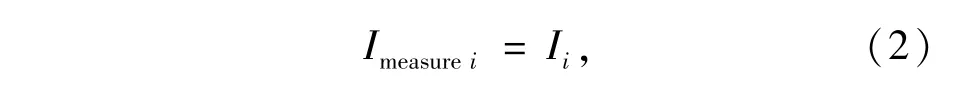
式中，i=1，2，3，……；Imeasurei为第i次调焦后用于评价函数计算的图像；Ii为第i步调焦后探测器获得的图像；I0为初始位置的离焦图像。

采用公式（1）和（2）得到的图像比较如图1所示。

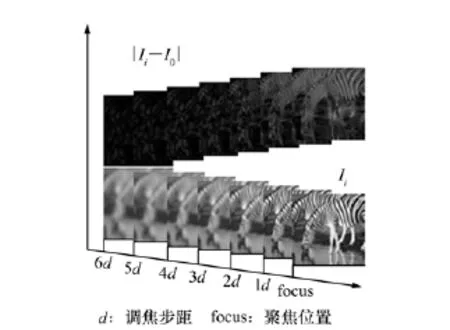
图1 式（1）和（2）的待评价图像比较图Fig.1 Comparison of images using algorithm （1）＆amp；（2）

由图1可看出，经绝对差分的图像的低频冗余被有效剔除，用于清晰度评价的图像仅包括边缘锐度较大的部分；随着离焦量的减小，差分图像的边缘锐度逐渐增强，调焦时具备可评价性。与此同时，提出的差分式方法在剔除图像低频冗余影响的同时，可以有效剔除CCD探测器的固有共模干扰。

3 评价区域选取

对于高分辨率、多像素的成像系统来说，对整幅图像进行评价函数计算将耗费大量的时间，影响调焦系统的实时性；同时，图像中的背景信息会严重影响聚焦图像的空间频率分布，导致评价函数的灵敏度和分辨率下降［11］。因此，选取整幅图像中边缘最丰富、锐度最强的部分进行评价函数计算是必要的。

3.1 评价区域的选取判据

本文用于区域选择的图像为|I1-I0|，而在调焦过程中，获得的首幅和次幅图像的绝对差分|I1-I0|中的边缘信息灰度往往较低，但这些边缘信息却对应着原始景物中的边缘锐度最大的部分，因此要对其进行提取和增强。鉴于此，构造评价区域选取判据为：

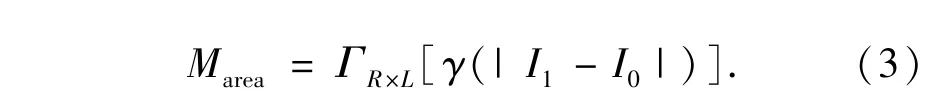
其中γ（）为图像的边缘轮廓获取函数，选用“sobel”算子对图像进行轮廓提取并进行二值化处理；ΓR×L［］为轮廓信息能量最大值窗口获取函数，R和L分别为评价窗口的行和列数。R和L值应选择适当，若过大会起不到降低调焦时间的作用，若过小则会导致评价函数不稳定，这里取值为R=L=100，读者可根据相机实际像元数自行选取。

评价区域选择方法可由图2形象表示。

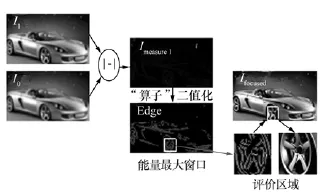
图2 评价区域选取原理示意图Fig.2 Sketch map of evaluation area selection

图2中，评价区域Marea是通过在图像Edge中遍历搜索灰度能量最大的窗口而得到的，它代表了景物中边缘锐度最强的部分。但对于图像大小为M×N、评价窗口为m×n的调焦系统，当采用遍历法进行聚焦区域搜索时，须对（M-m+1）×（N-n+1）个子图像进行边缘能量计算，计算量极大。因此，本文采用微粒群算法（Particle Swarm Optimization，PSO）进行寻优。

3.2 评价区域的PSO搜索算法

PSO算法［12］是Kennedy和Eberhart于1995年提出的一种基于群智能的演化计算技术，主要用于搜索全局最优解。其核心思想是：通过群体中个体之间的协作和信息共享来寻找全局最优解。PSO算法初始化为一群随机粒子，粒子在每一次迭代中通过跟踪两个“极值”（粒子当前时刻为止的个体最优解p和粒子种群当前时刻为止的全局最优解g）来更新自己，通过不断地学习与迭代，最终达到全局最优解。采用标准PSO算法，粒子速度和位置的迭代公式为：

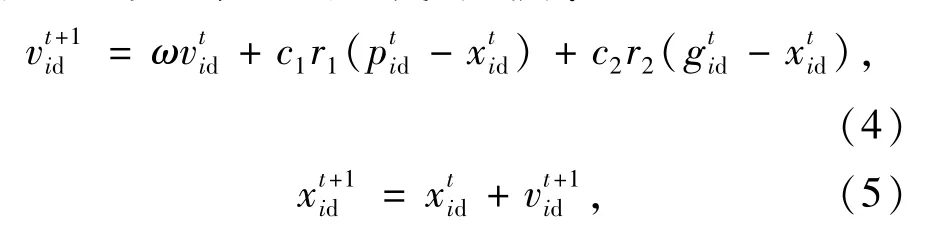
式中，i=1，2，…，K表示粒子数序号；ω为惯性权重；c1，c2为加速系数；r1，r2是［0，1］间的随机数。PSO算法的详细计算步骤及参数选取参见文献［13］。

本文的搜索目标是寻找图像中的最佳评价区域。对于窗口大小确定的调焦系统，评价区域的位置可由其左上角像素坐标（x，y）唯一确定，因而将粒子的维数设为二，分别对应评价区域左上角像素的横纵坐标，这样一个粒子就代表了一个评价窗口。对于图像大小为M×N、评价窗口大小为m×n的调焦系统，PSO粒子种群定义为：

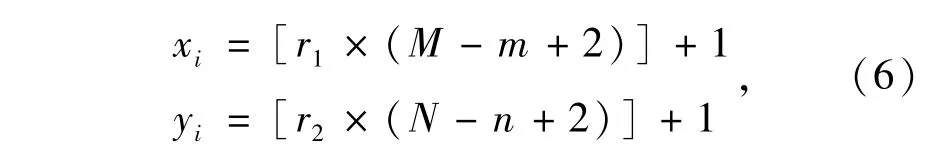
其中，［］高斯取整函数，r1，r2是［0，1］间的随机数，（x1，yi）为第 i个粒子的位置；i=1，2，…，K。速度初始化亦为随机值。适应度函数为：

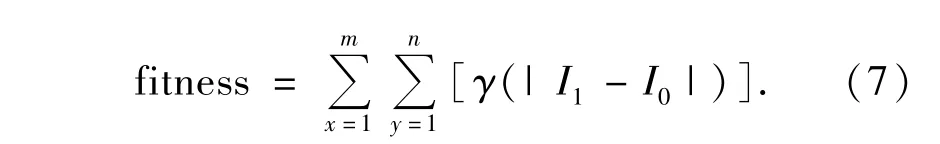
图3 聚焦区域的微粒群算法搜索结果Fig.3 Search results in focusing area by PSO

同时，本文选取K=30，c1=c2=2，ω=0.5，终止条件M=25，可根据具体情况自行调整。利用PSO对某图像进行评价区域自动搜索，结果如图3所示。

从图3可以看出，PSO算法的搜索结果对应着原图像中边缘最丰富的部分，经过数据计算也证明了PSO算法获得了该图像中的全局最优解（29，133）。然而PSO算法属于随机式启发算法，对于复杂的多峰函数，其搜索结果与粒子的初始值有关，而初始值为随机数，因此有时可能得不到全局最优解。所以在应用PSO算法对图像的评价区域进行搜取时，有必要验证其准确性和稳定性。

由概率统计中的大数定律可知，对于一个随机事件，当实验次数足够多时事件结果的算术平均值依概率收敛于真实值。蒙特卡洛（Monte Carlo）方法正是建立在这一理论基础之上的。该方法先根据实际问题建立模型，再按照设定的随机过程反复生成随机数，通过求输出结果的统计特征值作为待解问题的数值解。本文采用蒙特卡洛分析的思想对PSO区域选取的结果进行统计，对同一幅图像做1 000次区域选取实验，实验结果用输出区域左上角像素的坐标来表示，每次实验时粒子初始值的随机数按乘同余法生成，得到的前8次结果如表1所示。

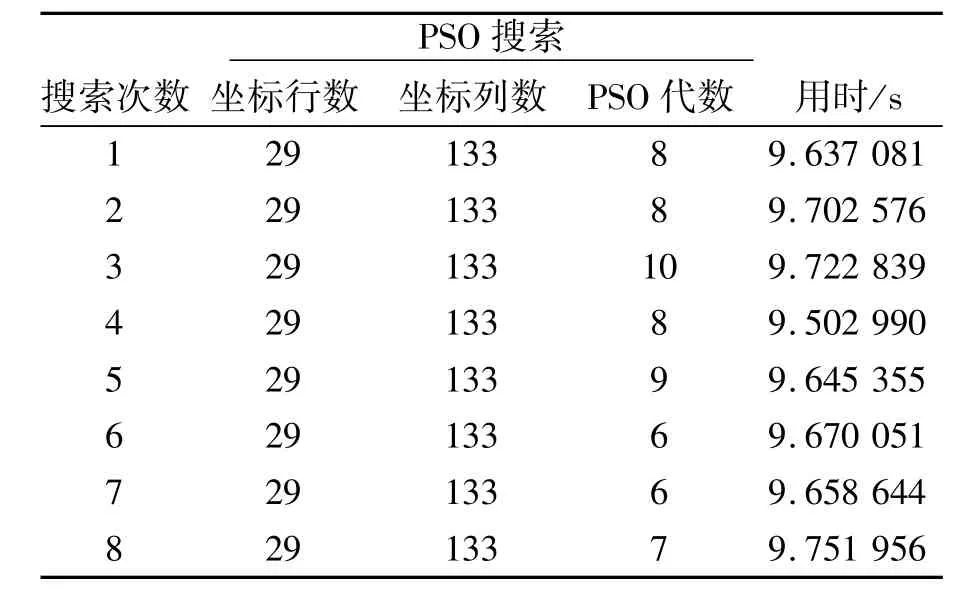
表1 PSO算法寻优结果Tab.1 Optimization results by PSO method

表1中遍历法搜索坐标行数为29，坐标列数为133，对应的搜索曲线如图4所示。

由表1和图4可以看出，虽然各次搜索的粒子初始化位置随机、初始适应度各不相同，但PSO搜索算法能在极少的代数内找到全局最优解，没有出现陷入局部极值的现象。整个实验得到的结果均值为（28.993，132.982），准确率为99.97％，与采用遍历法获得的全局最优值几乎相等，比文献［11］中的自适应遗传算法稳定性高。从计算时间来看，文献［11］中遗传算法自身的选择、交叉和变异策略需要较多计算时间，相比之下，PSO算法的更新机制简单，计算量要小。本文在主频为1.73 GHz、内存为1 G的PC机上对搜索方法进行仿真，前8次用时如表1中所示，1 000次平均用时约为9.51 s，平均搜索代数约为7，对文献［11］和本文方法的聚焦窗口大小和硬件速度进行等效转换和比较表明，本方法平均用时约为126 ms，更适合调焦使用。

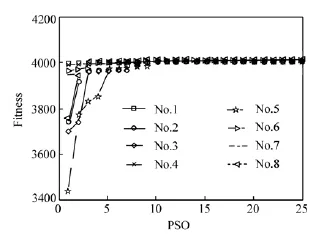
图4 PSO算法搜索适应度曲线Fig.4 Fitness values of searching by PSO

4 基于Wavelet的评价函数

小波变换［14，15］（Wavelet Transforms）是继Fouirer变换以来的纯粹数学和应用数学完美结合的一个典范，具有优秀的时频局部特性，对图像边缘细节的锐度信息有很强的提取能力和感应灵敏度。

4.1 评价函数构造

图像小波分解可由图5表示（以3层分解为例）。

从图5中可以看出，在每一层分解过程中，二维小波将图像分解为低频和高频两部分，其中高频包括HH、HL和LH 3个分量。同时，各层分解均可得到 4组分解系数 coefLHK（低频系数）和coefHHK，coefHLK，coefLHK（高频系数）。 高频系数代表了各分辨率下高频成分的能量和强度。在聚焦过程中，高频能量逐渐增强，低频能量缓慢衰减。综上所述，构造基于 Wavelet的评价函数如式（8）：

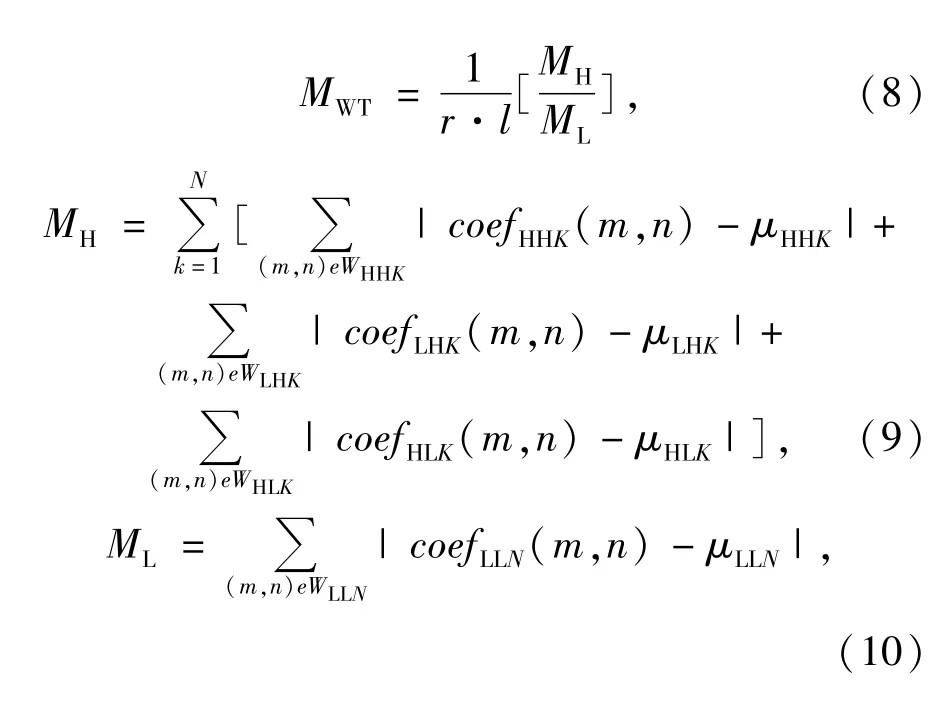
式中，r和l分别为用于分解的图像的行和列数，N为小波分解层数，μ为各层系数的数学期望；W为各层分解得到的窗口图像。

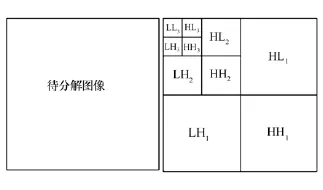
图5 二维小波分解示意图Fig.5 Sketch map of two-dimensional wavelet transforms

4.2 评价函数参数选取

与传统小波评价函数中参数的选取不同，本文的选取要适应公式（1）所得到的图像的特点。

4.2.1 小波基的选取

小波基的支撑长度和消失矩是两个重要的参数。支撑长度决定了小波基的时频局域化能力和计算复杂度；消失矩则表征了小波基逼近光滑信号时的收敛率，体现了对奇异点的捕捉能力。因此，二者对小波基的高频细节提取能力均有影响，通常希望选用支撑长度短、消失矩高的小波基。

选用工程中应用较为广泛的 Db（Daubechies）、Coif（Coiffets）和Sym（Symlets）小波进行对比实验。其中，3种小波基的主要参数特性比较如表2。

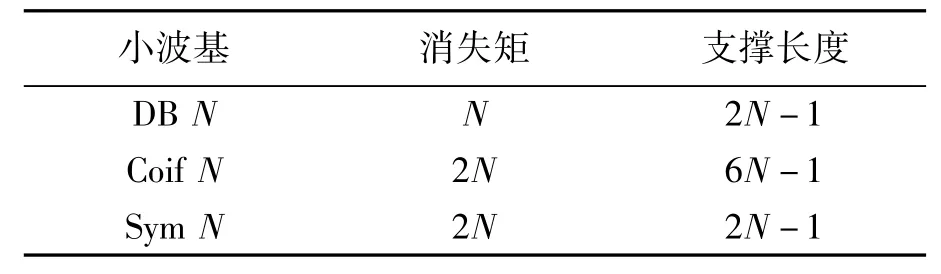
表2 小波基参数特性比较Tab.2 Characteristics comparsion of wavelets

为方便起见，分两步进行比较（评价函数曲线形态优劣判据采用文献［6］中提出的自动聚焦不确定性测量（AUM）判据，AUM值越小，曲线形态越佳，同时，本文调焦步距为d=4 μm（为方便起见这里不采用变步长调焦））。

第一步：取相同的支撑长度（L=5），分解层数为3，并采用第4.1节提出的评价函数和差分式提取方法对Lena图像聚焦序列进行分析，此时，对应的小波评价函数曲线归一化（用每步值除以最大值）后如图6所示，对应的AUM判据值如表3所示。

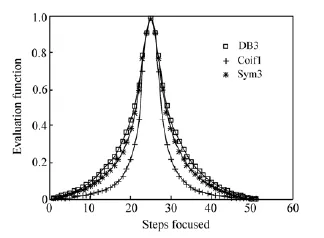
图6 等支撑长度小波基评价效果比较Fig.6 Comparison of wavelet assessing effects with the same support length L

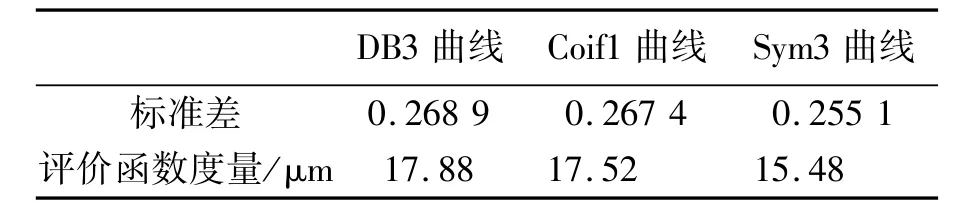
表3 图6评价函数曲线标准差和AUM值Tab.3 Standard deviation and AUM values of evaluation function in Fig.6

由表3可知，Sym小波的评价函数曲线的AUM值最小，因此平均分辨率最高；同时，由于L=5，因此3种小波基的消失矩分别为3，2和6，所以Sym小波的消失矩也是三者中最高的。

第二步：取相同的消失矩（D=4），其他条件同第一步，各评价函数曲线归一化后如图7所示，对应的AUM判据值如表4所示。

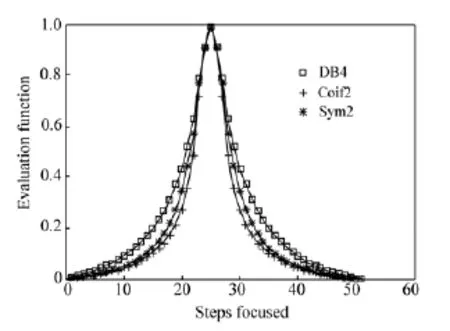
图7 等消失矩小波基评价效果比较Fig.7 Comparison of wavelets assessing effects with the same D

表4 图7评价函数曲线标准差和AUM值Tab.4 Standard deviation and AUM values of evaluation function in Fig.7

由表4可知，Sym小波的评价函数曲线的AUM值最小，因此平均分辨率最高；而且D=4时，3种小波的支撑长度分别为7，11和3，因此Sym小波的支撑长度最短，计算量最小。

综合上述两步仿真分析，选用Sym小波族。接下来确定N值。

由表2可知，N值决定了小波基的消失矩和支撑长度的大小。N值选取应适中，过小则消失矩过低，过大则支撑长度过长，计算量太大，因此取N为2，4，6，8，其他条件同第一步，比较结果如图8所示，对应的AUM判据值如表5所示。

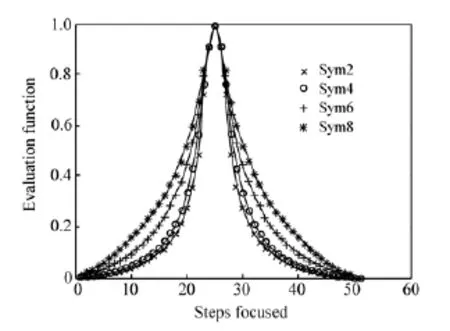
图8 不同N值的Sym小波基评价效果比较Fig.8 Comparison of wavelet assessing effects with different N

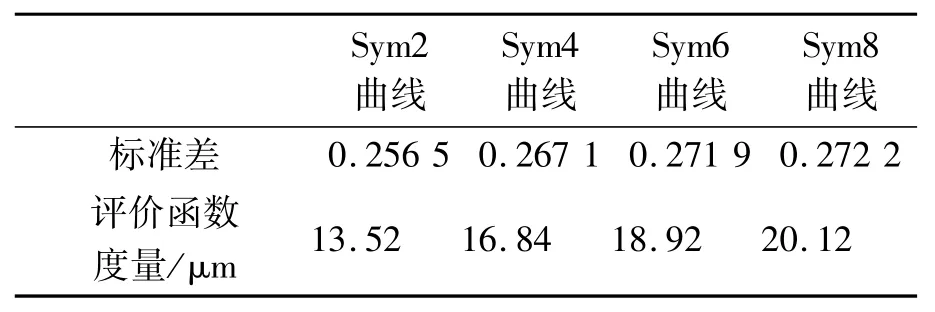
表5 图8评价函数曲线标准差和AUM值Tab.5 Standard deviation and AUM values of evaluation function in Fig.8

由表5可知，Sym2的评价函数曲线的AUM值最小，平均分辨率最高，因此本文选取Sym2小波基。

4.2.2 分解层数的确定

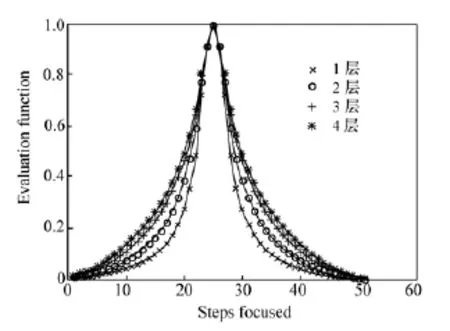
图9 不同分解层数评价效果比较Fig.9 Comparison of evaluation effects with different decompose floors

选取分解层数1、2、3和4进行比较，并采用第4.1节提出的评价函数和差分式提取方法对Lena图像聚焦序列进行分析，比较结果如图9所示，对应的AUM判据值如表6所示。

表6 图9评价函数曲线标准差和AUM值Tab.6 Standard deviation and AUM values of evaluation function in Fig.9

由表6可知，1层分解的评价函数曲线的AUM值最小，平均分辨率最高，因此本文选取分解层数为1。

5 实验与比较分析

经上述三节介绍，本调焦方法流程如图10所示。

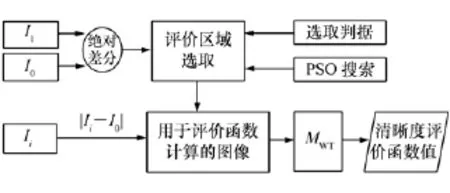
图10 自动调焦方法流程图Fig.10 Flow chart of auto-focusing method

5.1 与传统调焦方法的比较

传统的调焦方法在I0图像中进行评价区域选择，目前典型的选取方法包括固定窗口（中心取窗法、黄金分割法等）和自适应窗口（基于图像熵的选取方法和基于图像一阶矩的选取方法等）。然后通过传统的评价函数［6～10］进行图像清晰度评估，本文选用了功率谱函数（公式（11））、熵函数（公式（12））、灰度差分函数（公式（13））和传统的小波评价函数法（公式（14））4种典型的传统评价函数。

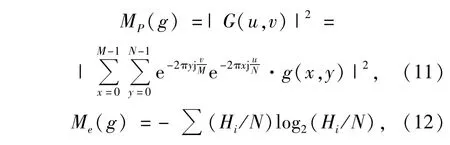
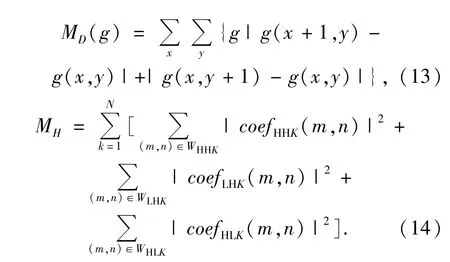
而本文方法则在图像|I1-I0|中利用PSO算法和判据公式（3）搜索评价窗口区域，然后以公式（8）作为评价函数。由于传统方法的组合方式较多，为方便起见，做比较试验如下：

（1）与固定窗口调焦比较（以中心窗口为例）

由于固定的评价窗口不具备自适应性，可能存在窗口内景物边缘细节稀少的情况，此时本方法与各传统评价函数比较如图11所示。由图11可以看出，由于固定窗口内细节与边缘较少，各传统调焦曲线均很平缓，传统小波方法和熵函数法甚至出现拐点，无法用于调焦，其他方法的评价函数的AUM值如表7所示。

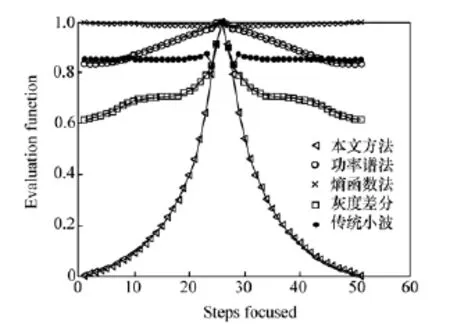
图11 固定窗口中细节稀少时的评价曲线图Fig.11 Evaluation curves with little details in fixed window

表7 图11评价函数曲线标准差和AUM值Tab.7 Standard deviation and AUM values of evaluation function in Fig.11

由此可见，本方法的 AUM值最小，曲线最好。

在某一固定离焦位置分别重复进行100次聚焦试验，3种方法的平均聚焦时间及平均聚焦精确度如表8所示。其中，聚焦精度为理想聚焦位置与实际聚焦位置差的绝对值，聚焦精度由控制系统精度决定。

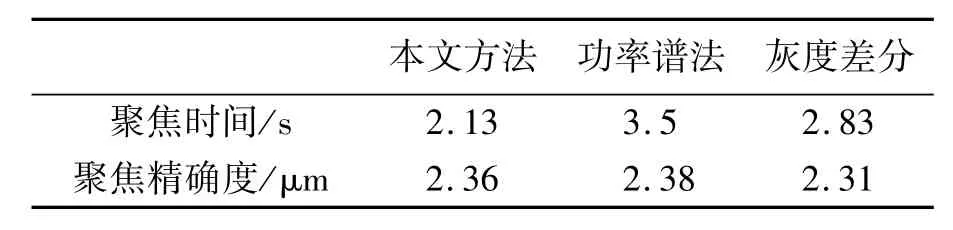
表8 3种方法的聚焦时间及聚焦精确度比较Tab.8 Comparison of focusing time and focus precision of three methods

由表8可知，与固定窗口的传统方法相比，本方法的聚焦时间最短，聚焦精度无大差异。

当窗口内景物存在足够细节和边缘时，本方法与传统各评价函数比较如图12所示。对应的AUM判据值如表9所示。

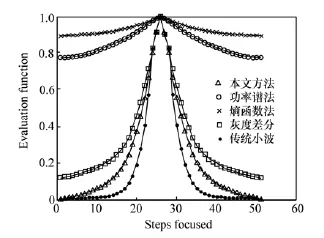
图12 固定窗口中细节稀多时的评价曲线图Fig.12 Evaluation curves with much details in fixed window

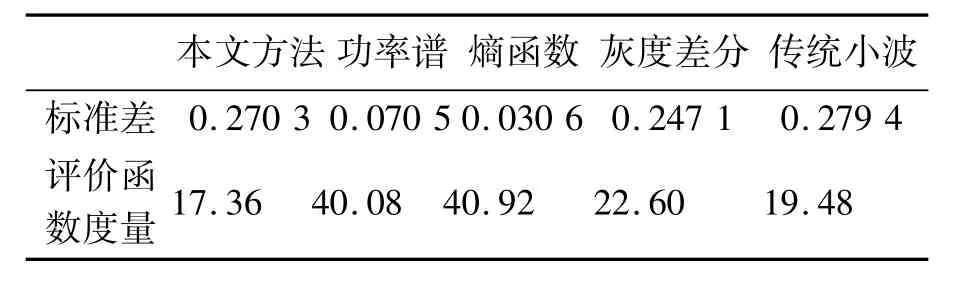
表9 图12评价函数曲线标准差和AUM值Tab.9 Standard deviation and AUM values of evaluation function in Fig.12

由此可见，本方法的AUM值最低，评价函数曲线最好。

（2）与自适应窗口调焦比较（以基于熵的方法［11］为例）。

由于采取了基于熵的评价区域选取方法，本方法和此时的传统方法在评价区域的获取结果上差异不大，此时的比较结果如图13所示，对应的AUM判据值如表10所示。

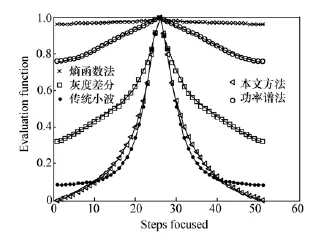
图13 自适应窗口时的评价曲线图Fig.13 Evaluation curves with adaptive window

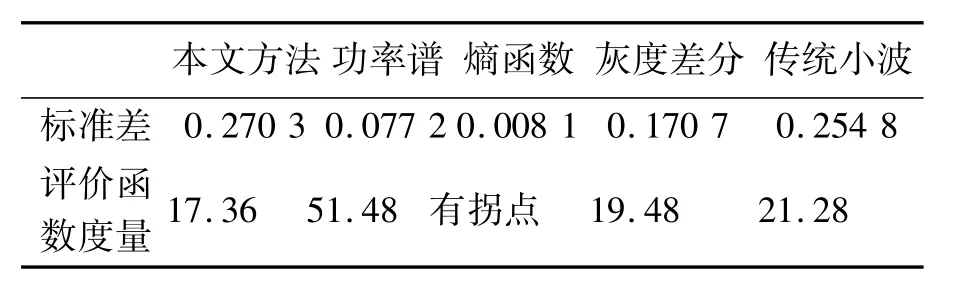
表10 图13评价函数曲线标准差和AUM值Tab.10 Standard deviation and AUM values of evaluation function in Fig.13

由此可见，本方法的 AUM值最小，曲线最好。

在某一固定离焦位置分别重复进行100次聚焦试验，除熵函数法有拐点外，其他方法的平均聚焦时间及平均聚焦精确度如表11所示。

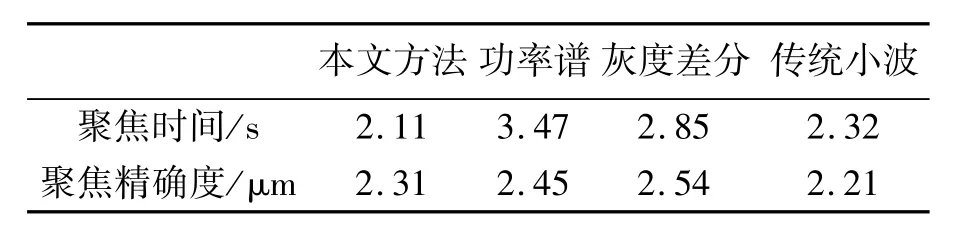
表11 图13评价函数曲线标准差和聚焦精确度Tab.11 Standard deviation and focus precision values of evaluation function in Fig.13

由表11可知，与自适应窗口的传统方法相比，本方法的聚焦时间最短，聚焦精度无大差异。

5.2 初始位置影响分析

由于本方法中用于评价函数计算的图像是通过差分式提取得到的，因此不难想象，初始位置不同时，差分获得的前几次图像灰度以及所包含的边缘信息的丰富程度会有所不同。以此类推，整个评价函数曲线的形态亦会有所不同，这也是本方法与传统方法的一个主要区别，也就是说本方法的调焦曲线是随初始位置而变化的。本文对Lena图像序列进行了仿真，结果如图14所示。

由图14可知，初始位置不同时评价函数归一化曲线形态确有不同，且初始离焦量越小曲线越陡峭；同时，不论初始位置如何，本方法的曲线均能几乎充满［0，1］区间（即初始位置处的评价函数值接近于0），使得本方法具有较高的平均调焦分辨率。最后，观察图12、图13和图14，可以发现，除本方法，其他方法均无法充满［0，1］区间，这也是本方法优于传统方法［16，17］的主要特点。

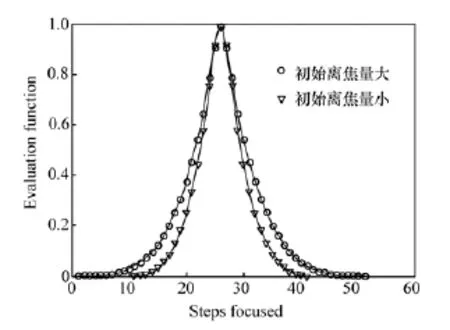
图14 不同初始位置评价效果比较Fig.14 Comparison of assessing effects with different original positions

6 结 论

本文提出了差分式提取图像边缘的方法，给出了基于微粒群边缘能量搜索的聚焦区域选取途径，并构造了图像清晰度的小波评价函数。通过实验比较，选用了Sym2小波基，并确定分解层数为1层；采用公式（1）的待评价图像获取方法和小波评价函数相结合的方式与传统方法进行了对比实验，结果表明，前者具有最大的调焦范围和很高的分辨率，同时，PSO算法的使用，进一步提高了聚焦的速度，而且本文调焦方法不受初始位置的影响。

［1］NAYAR S K，NAKAGAWA Y.Shape from focus［J］.IEEE T.Pattern Anal，1994，16（8）：824-831.

［2］PARK B-K，KIM S S，CHUNG D S，et al..Fast and accurate auto focusing algorithm based on two defocused images using discrete cosine transform［J］.SPIE，2008，6817：68170D.

［3］CHOI J S，KANG H，LEE C M，et al..Noise insensitive focus value operator for digital imaging systems［J］.IEEE Transactions Consumer Electronics，2010，56（2）：312-316.

［4］KIM Y，LEE J S，MORALES A W.A video camera system with enhanced zoom tracking and auto white balance［J］.IEEE Transactions Consumer Electronics，2002，48（3）：428-434.

［5］MICHELE M，HENRY J，FREDERICK K，et al..A Image based auto-focusing algorithm for digital fundus photography［J］.IEEE Transactions Medical Imaging，2009，28（11）：1703-1707.

［6］SUBBARAO M，TYAN J K.Selecting the optimal focus measure for auto-focusing and depth-from-focus［J］.IEEE T.Pattern Anal.，1998，20（8）：864-870.

［7］SUN Y，DUTHALER S，NELSON B J.Auto-focusing in computer microscopy：selecting the optimal focus algorithm［J］.Microscopy Res.Techniques，2004，65（3）：139-149.

［8］YANG G，NELSON B J.Wavelet-based auto-focusing and unsupervised segmentation of microscopic image［C］.Proceedings of the IEEE International Conference on Intelligent Robots and System，Las Vegans，Nevada，2003：2143-2148.

［9］张乐，姜威，高赞.数字图像一阶矩的自动聚焦区域选择算法［J］.光学技术，2008，34（2）：231-236.ZHANG L，JIANG W，GAO Z.Automatic focusing region selection algorithm based on first order of digital image［J］.Opt.Technique，2008，34（2）：231-236.（in Chinese）

［10］梁敏华，吴志勇，陈涛.采用最大灰度梯度法实现经纬仪自动调焦控制［J］.光学 精密工程，2009，17（12）：3016-3021.LIANG M H，WU ZH Y，CHEN T.Auto-focusing adjustment of theodolites by largest the Gradient method［J］.Opt.Precision Eng.，2009，17（12）：3016-3021.（in Chinese）

［11］胡涛，陈世哲，刘国栋，等.图像法自动调焦的最佳调焦区域选取算法［J］.光学技术，2006，32（6）：851-854.HU T，CHEN SH ZH，LIU G D，et al..Algorithm of selecting the optimal focusing region［J］.Opt.Technique，2006，32（6）：851-854.（in Chinese）

［12］KENNEDY J，EBERHART R.Particle swarm optimization［C］.Proc IEEE Int Conf on Neural Networks，Perth，Australia.Nov/Dec 1995：1942-1948.

［13］谢晓锋，张文俊，杨之廉.微粒群算法综述［J］.控制与决策，2003，18（2）：129-134.XIE X F，ZHANG W J，YANG ZH L.Overview of particle swarm optimization［J］.Control and Decision，2003，18（2）：129-134.（in Chinese）

［14］JAWERTH B，AWELDENS W.An overview of wavelet based multiresolution analysis［J］.SIAM Rev.，1994，36（3）：377-412.

［15］XIE H，RONG W B，SUN L N.Wavelet-based focus measure and 3-D surface reconstruction method for microscopy images［C］.Proc.of the IEEE/RSJ International Conference on Intelligent Robots and Systems，Beijing，China，2006：229-234.

［16］张运海，赵改娜，张中华，等.免散瞳眼底照相机的精密调焦［J］.光学精密工程，2009，17（5）：1014-1019.ZHANG Y H，ZHAO G N，ZHANG ZH H.Accurate focusing of non-mydriatic fundus camera［J］.Opt.Precision Eng.，2009，17（5）：1014-1019.（in Chinese）

［17］张新洁，颜昌翔，谢涛.星载光学遥感器调焦机构的设计［J］.光学 精密工程，2009，17（11）：2756-2761.ZHANG X J，YAN CH X，XIE T.Design of focusing mechanism of space remote sensor［J］.Opt.Precision Eng.，2009，17（11）：2756-2761.（in Chinese）

Difference auto-focusing based on particle swarm optimization searching and wavelet evaluation

LÜ Heng-yi1，LIU Yang2，XUE Xu-cheng1

（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Department of Control Science and Engineering，Harbin Institute of Technology，Harbin 150001，China）

In order to enhance the auto-focusing capability of a imaging system，a difference image extraction method is proposed.Meanwhile，a evaluation function based on wavelets and a region selecting technique using Particle Swarm Optimization（PSO）are given.The principle and superiority of the difference image extraction method are introduced.Then a selecting criterion and a searching method using PSO for region evaluation are described，and the parameters for wavelet based evaluation function are compared and optimized.Finally，emulation experiments are practiced to analyze the advantages and disadvantages of traditional and proposed methods.Results indicate that the proposed method can offer a higher resolution to the focusing curve due to the difference image extraction，new focusing window and focus evaluation.Moreover，it has improved the focusing speed by 170 ms and provided the focusing precision about 2.3 μm.Furthermore，its focusingeffects are always satisfactory with different initial positions.

auto-focusing；difference edge extraction；focus region selection；Particle Swarm Optimization（PSO）；defination evaluation function；wavelet transform

TP391.4

A

1674-2915（2011）03-0283-10

2011-02-21；

2011-04-23

国家自然科学基金重大合作项目（No.6071002）

吕恒毅（1984—），男，辽宁大连人，硕士，研究实习员，主要从事空间遥感相机成像系统及智能调焦等方面的研究。E-mail：lv_hengyi@163.com

刘 杨（1982—），博士研究生，主要从事信号处理和故障诊断方面的研究。E-mail：lghit520@yahoo.com.cn