基于改进灰色模型的电力负荷中长期预测

蒋 燕，谢 林，李子清，陈 刚

(1.重庆电力高等专科学校电力工程系，重庆400053;2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044)

0 引言

负荷预测是电力系统运行和规划的前提，它对电力系统调度、用电、计划等工作有着重要的意义［1］。提高负荷预测精度一直是一些学者和工程师所追求的目的。

负荷预测的核心是预测方法的选择，也就是建立预测数学模型［2］。常见的中长期负荷预测方法大致分为两大类。一类是基于参数模型的预测方法，常见的有:电力弹性系数法、时间序列法、相关分析法、回归分析法等［3］。第二类是基于非参数模型的预测方法，常见的有:灰色模型预测法、模糊预测法、人工神经网络预测法、小波分析法、优选组合预测技术、专家预测技术等。

灰色GM(1，1)预测模型是电力系统负荷预测中最常用的模型。它把一切随机过程看作是在一定范围内变化的、与时间有关的灰色过程，将离散的原始数据整理成具有规律性的生成数列，使其生成序列呈一定的规律，并用典型曲线拟合建立数学模型。

灰色模型法由于具有所需数据少、计算量小的优点而得到了广泛的应用［4］。然而，传统的灰色模型并非是一种严格的系统方法，它避开了影响负荷数据变化的一些因子，它的建模是一种近似指数增长规律模型，当负荷增长率变化较大时，预测精度较低。且预测模型过多的依赖数据初始取值，初始值的微小变化都可能使模型变化很大。因此在数据波动性比较大时，使得预测效果不是很理想。

本文对灰色模型进行了一定的改进，首先对负荷数据进行灰色建模，得到灰色负荷预测值，然后与实际负荷数据对比得到数据差序列，最后再对数据差序列进行线性回归建模，对未来年数据差值进行预测，并加上灰色模型所预测值得到最终的修正值。此方法的优点在于避免了仅仅靠灰色模型进行预测而未对残差进行修正的缺点，并且线性回归算法简单，提高了其结果预测精度。

1 灰色模型基本原理

灰色系统理论是我国著名学者邓聚龙教授于1982年创立的一门新兴横断学科，它以“部分信息己知、部分信息未知”的“小样本”、“贫信息”不确定系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统行为的正确认识和有效控制。在灰色系统理论的创立和发展过程中，邓聚龙教授发现并提炼出灰色系统的基本原理。这些基本原理具有十分深刻的哲学内涵［5］。

灰色系统是采用数据生成，并从生成中寻找数学规律的一个边缘学科。数据生成是指将原始数列X(0)中的数据x(0)(k)按某种方法作数据处理(或数据变换)。灰色理论对灰量、灰过程的处理，不是找概率分布，求统计规律，而是用“生成”的方法求得随机性弱化、规律性强化了的新数列，此数列的数据称为生成数。利用生成数建模，是灰色理论的重要特点之一。

GM(1，1)模型的实质是对原始数据序列作一次累加生成(1-AGO)，使生成数据列呈现出指数增长的规律，并建立微分方程模型，最后求解微分方程的时间响应函数表达式，再累减还原可得到预测值。

GM(1，1)建模的具体步骤如下:

①设原始数据序列为:

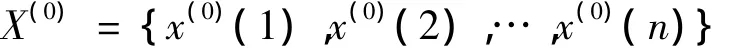
对X(0)数据列进行一次累加生成(1-AGO)，得到新的数据列 {x(1)(k)}，k=1，2，...，n ，即:

②记X(1)={x(1)(k)}，建立一阶线性灰色微分方程的白化微分方程:

③利用最小二乘法则求解模型参数a，u:

其中:

不对称故障情况下，由于负序分量的存在，锁相环无法跟踪实际的换相电压而产生偏移，同时换流器交流侧和直流侧分别会产生较大含量的三次谐波和二次谐波，交流侧电压三次谐波会进一步影响换相电压的过零点偏移，可能会导致换流阀延迟导通进而影响实际触发角；交流侧电压三次谐波和直流侧电流二次谐波影响换相持续时间从而影响换相角。因此本研究基于换流器交流侧发生不对称故障，分析了换流器的实际触发及换相过程，通过对实际触发角和换相角的计算得到实际熄弧角来判断是否发生换相失败，并给出了详细的计算流程，具有一定的理论价值和工程应用价值。

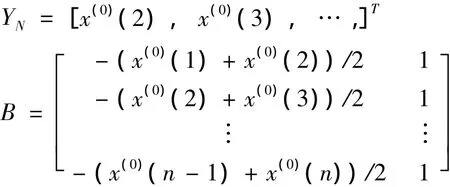
④求解微分方程，得灰色预测模型:

⑤还原为X(0)的灰色预测模型:

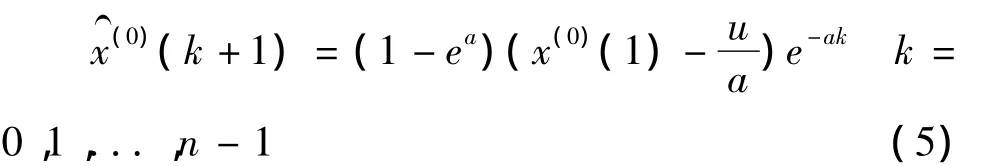
2 改进的灰色预测模型

为进一步提高预测精度，本文根据电力负荷预测的特点，针对常规灰色模型预测存在的不足，从以下两个方面对常规灰色模型进行改进:一是对负荷原始数据进行平滑处理;另一方面，采用一阶线性回归模型对灰色模型的预测结果进行修正。

2.1 数据平滑处理

常规的灰色预测模型GM(1，1)是一种指数增长模型，当电力负荷累加数据呈现严格的指数增长形势时，则用此方法通常能够保证较好的数据拟合度。但是当数据波动性变化较大，不够平滑时，常规方法的预测误差可能变得较大［7］。因此为了降低数据的不平滑度，可采用了三点平滑数据处理技术对数据进行平滑处理，可使预测数据拟合度效果更好。

三点平滑公式如下:

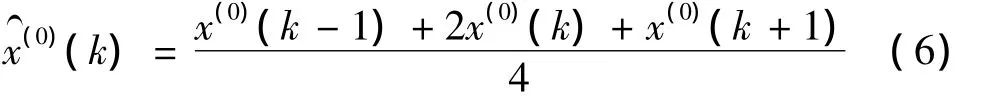
对于两端点计算公式分别为:

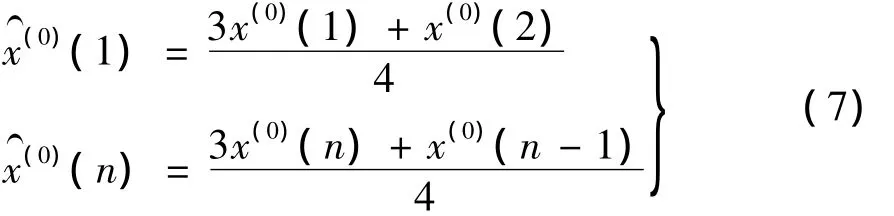
经过这样处理既增加了当前数据的权重，又避免了数值过度波动，使预测更加可信。然后再利用(5)式进行灰色模型建模。

2.2 残差修正处理

对序列 x(0)(k)，k=1，2，...，n ，按照 GM(1，1)模型方法求解出预测值(k)，算出残差序列{ε(0)(k)}，k=1，2，...，n ，其 中 ε(0)(k)=x(0)(k)-(k)。首先定义残差序列ε(0):

对该残差数据进行一元线性回归建模，得到ε(0)的线性回归模型为:

n

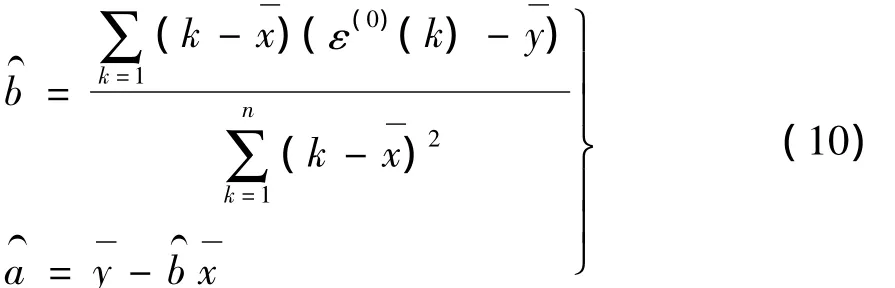
建立了残差数据的一元线性回归模型(9)后，可对灰色预测模型的(k)进行修正，即:

运用线性回归残差修正模型可以提高一般灰色预测模型的预测精度，并且避免了对残差符号的选择问题。

3 算例分析

为了验证此改进算法的有效性，以某地区1992～2002年共11年的历史年最大负荷［8］数据作为预测样本进行建模，并对2003～2005年年最大负荷进行预测。

x(0)=(25.44，28.21，30.22，31.65，35.41，37.21，41.60，46.85，48.32，49.82，50.52)

通过计算得到常规灰色模型方程为:

最后，对2007、2008、2009三年的年最大负荷进行预测，其预测值及相对误差结果见下表1。

表1 某地区年最大负荷预测结果及相对误差

从表1中可以看出，传统GM(1，1)的相对预测误差在10%左右，而采用改进灰色模型方法后，其预测误差保持在3%左右，误差大大的降低了，明显提高了预测精度。

4 结论

对传统灰色模型和改进灰色模型进行分析研究，通过具体算例比较分析可知，改进后的模型的预测精度更高，预测效果很好，验证了此方法的有效性。本文方法弥补了传统灰色理论本身具有的缺点，提高了预测精度，可用于电力系统中长期负荷预测。

［1］周维，晋红升，潘学华.混沌理论在中长期电力负荷预测中的应用［J］.中国电力教育，2007，(S3):87-8.

［2］黄家圣，谢卫，李军军，等.电力系统短期负荷预测的多神经网络集成模型［J］.上海海事大学学报，2005，(3):64-67.

［3］甄利玲.中长期电力负荷预测回归模型及其应用［J］.雁北师范学院学报，2002，(5):54-56.

［4］赵勇，李永刚.灰色理论在中长期负荷预测中的应用［J］.内蒙古科技与经济，2008，(2):83-84.

［5］邓聚龙.灰理论基础［M］.武汉:华中科技大学出版社，2002.

［6］牛勇，王震宇，王红军，等.改进灰色模型在中长期电力负荷预测中的应用［J］.东北电力大学学报，2009，(2).

［7］周晓刚.盘锦地区中长期电力负荷预测的研究［D］.沈阳:沈阳工业大学，2007.