边坡稳定分析的最小势能法与极限平衡法的对比研究
张 涓,陆 洋
(1.湖南工程学院 建筑工程学院,湘潭411104;2.中南大学 土木建筑学院,长沙 410075)
0 前 言
在公路、铁路等基础设施项目的建设过程中都会出现边坡工程,而边坡的稳定性直接影响到整个工程的质量.边坡稳定性分析的基本方法是极限平衡法,其基本特点是只考虑静力平衡条件和土的摩尔一库仑破坏准则,即通过分析土体在破坏那一刻的力的平衡来求得问题的解.在大多数情况下,问题是静不定的,极限平衡方法在处理静不定问题时的对策是引入一些简化假定,使问题变得静定可解.这种做法使方法的严密性受到了影响,但是对计算结果的精度影响并不大[1].
Mauldon和Ureta(1994)提出了一种新的滑动稳定性分析模型,此模型依据稳定平衡体系势能最小的原理,从整个边坡的势能变化求得一个满足势能最小的位移,据此可直接求出滑面上的法向应力分布,再利用平衡条件和摩尔-库仑强度准则便可直接得到安全系数[2].这种最小势能法思路清晰、计算简便,而通过它和传统的极限平衡方法的对比分析研究,有助于进一步了解其模型特点及适用范围.
1 边坡稳定安全系数的定义差别
最小势能方法和极限平衡法中的严格条分的Bishop法计算得到的安全系数非常接近.但是二者是两个完全不同的方法:二者的假设完全不同,在不同的假设前提下,二者沿滑裂面的法向力分布也不同;二者安全系数的定义也不同.最小势能法先假定一个扰动因素使土体从目前的稳定状态进入极限平衡状态.此时滑体内出现一假想的滑裂面,在该滑裂面上每一点的法向应力和切向应力都满足摩尔-库仑强度准则.最小势能方法的安全系数有超载系数的性质,即滑裂面上全部抗滑力矩和滑动力矩之比:
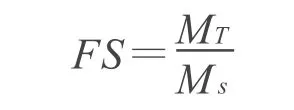
而Bishop法的安全系数,是通过降低材料的强度以达到极限平衡,是材料强度的储备系数[1].
2 算例分析
2.1 不同内聚力对计算结果的影响
选取如图1所示边坡,坡高3 m,坡比1∶1.2,容重 γ=20.5 kN/m3,内摩擦角 φ=15°,边坡控制点坐标:A(10,10),B(46,40),C(66,40),选取的滑弧半径51.8413 m,圆心O(18.6532,61.1140).在计算时忽略水和地震的作用.考虑锚索加固时的情况见图2[3]图中的锚索布置如表1.在不同内聚力下极限平衡法和最小势能方法得到的结果如表2和图3.表中MPE代表本文所用最小势能方法的结果,后同.
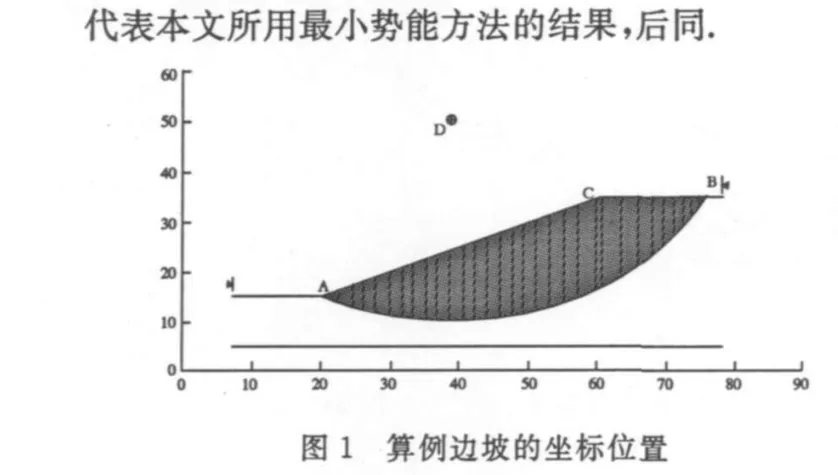
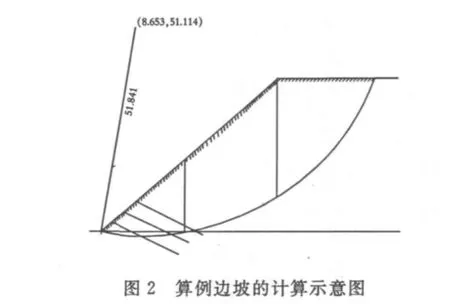

表1 锚索布置表
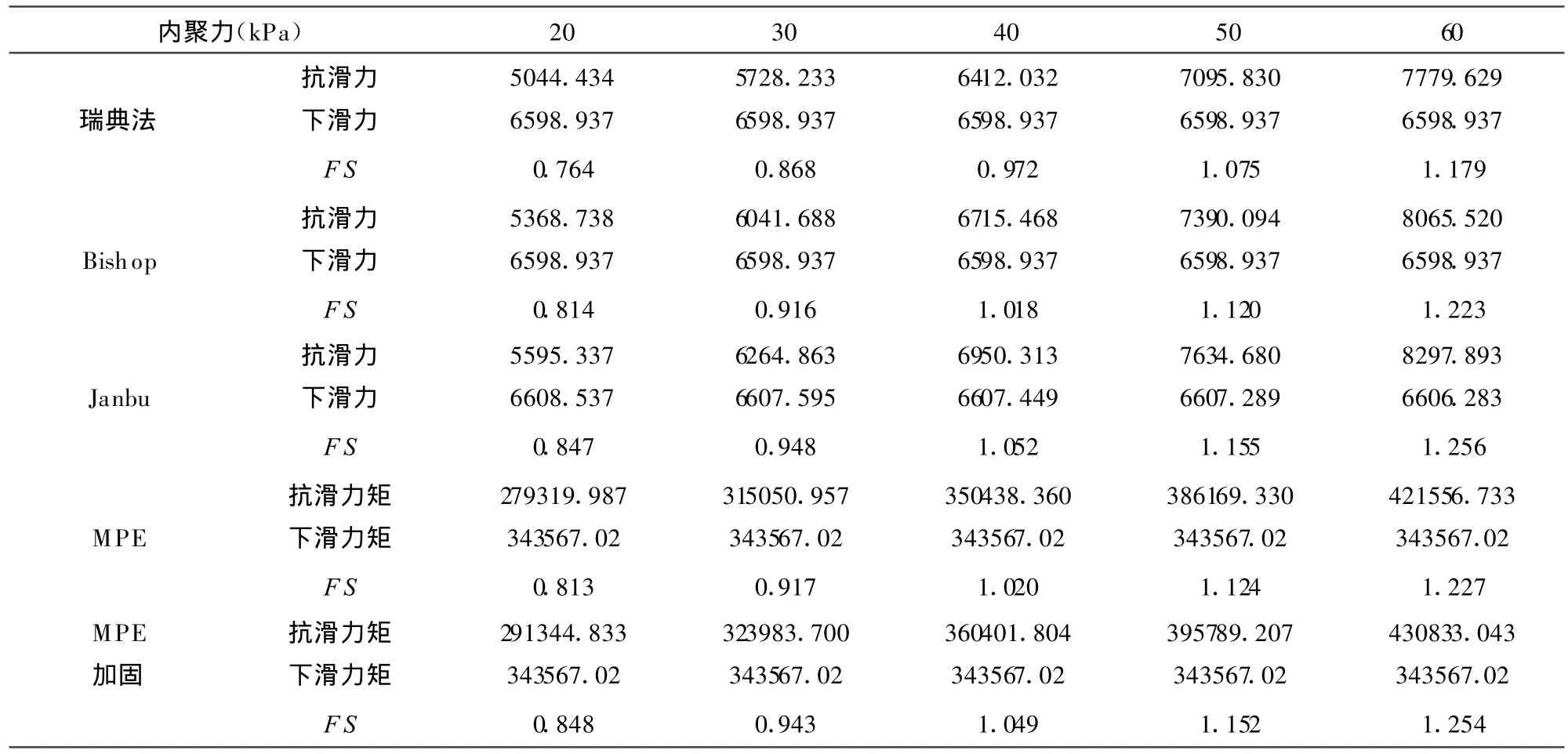
表2 不同内聚力下的计算结果
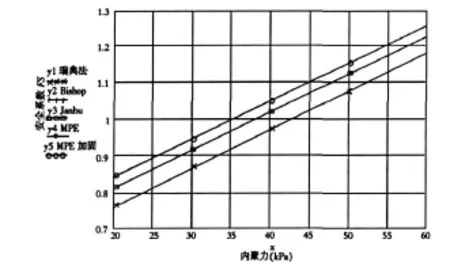
图3 不同内聚力下的计算误差比较
图3表明MPE法的计算结果与极限平衡方法的误差都比较小,原最小势能方法计算所得的安全系数和Bishop方法计算所得的安全系数十分接近.
2.2 不同内摩擦角对计算结果的影响
选取边界和图1同样的边坡,滑弧的位置不变,容重为γ=15 kN/m3,内聚力 C=35 kPa.将内摩擦角从10°等步长变为30°,比较极限平衡法和最小势能方法(MPE)得到的安全系数.计算结果如表3和图4所示.

表3 不同内摩擦角下的计算结果
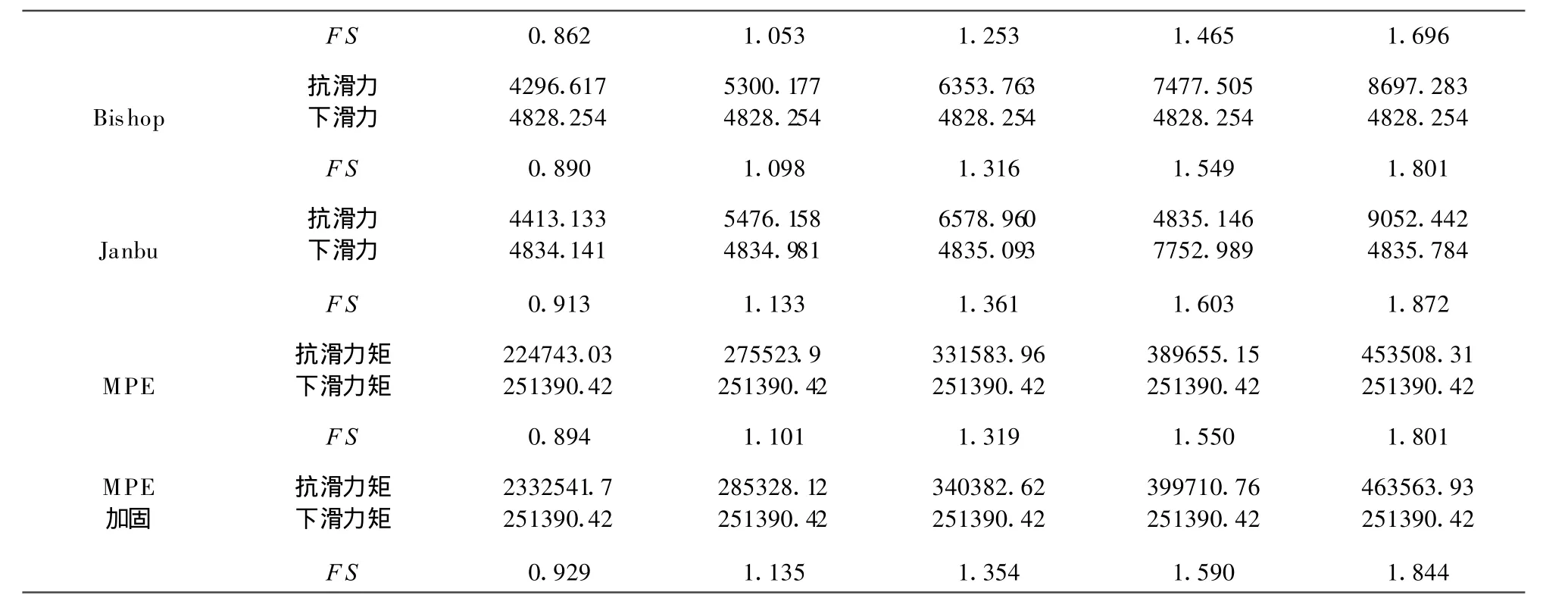
FS 0.862 1.053 1.253 1.465 1.696 Bishop Janbu抗滑力下滑力8697.283 4828.254 FS 0.890 1.098 1.316 1.549 1.801 4296.617 4828.254 5300.177 4828.254 6353.763 4828.254 7477.505 4828.254抗滑力下滑力9052.442 4835.784 FS 0.913 1.133 1.361 1.603 1.872 4413.133 4834.141 5476.158 4834.981 6578.960 4835.093 4835.146 7752.989 453508.31 251390.42 FS 0.894 1.101 1.319 1.550 1.801 MPE加固MPE抗滑力矩下滑力矩224743.03 251390.42 275523.9 251390.42 331583.96 251390.42 389655.15 251390.42抗滑力矩下滑力矩463563.93 251390.42 FS 0.929 1.135 1.354 1.590 1.844 2332541.7 251390.42 285328.12 251390.42 340382.62 251390.42 399710.76 251390.42
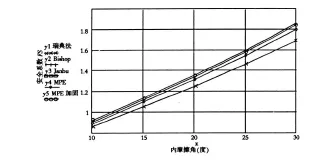
图4 不同内摩擦角下的计算误差比较
2.3 不同坡高对计算结果的影响
为测试不同坡高对最小势能法和Bishop法的安全系数的影响,设计图5所示边坡,坡比1∶1,内聚力C=15 kPa,内摩擦角 φ=22°,容重 18.4 kN/m3,设原始坡高为50 m,每次消去10 m,一直消到坡高为10 m,分别计算五种不同坡高下两种方法所得的安全系数.计算控制点坡脚坐标为0(8.778,10.1020),滑弧半径为70 m,圆心为(5,80).控制点1~10的坐标分别为:1(18.778,20.1020),2(28.778,30.1020),3(38.778,40.1020),4(48.778,50.1020),5(58.778,60.1020),6(72.112,60.1020),7(68.294,50.1020),8(62.517,40.1020),9(54.094,30.1020),10(41.225,20.1020).计算结果如表4和图6所示.
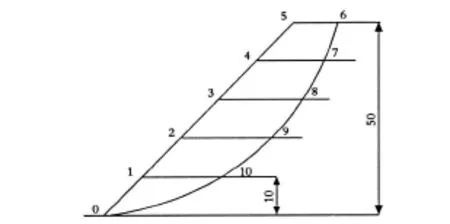
图5 不同坡高对安全系数的影响示意图
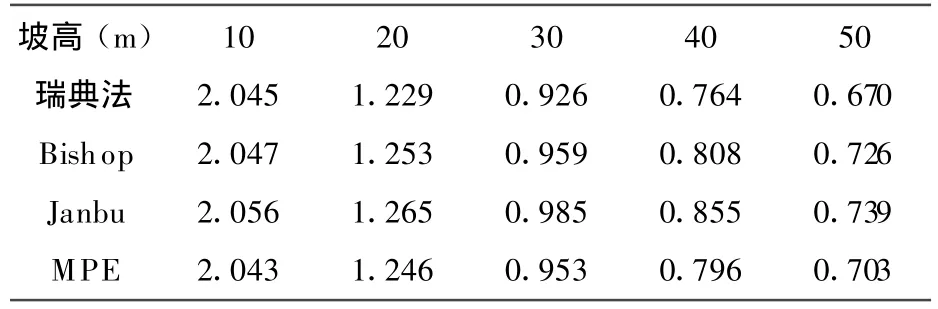
表4 不同坡高下的计算结果
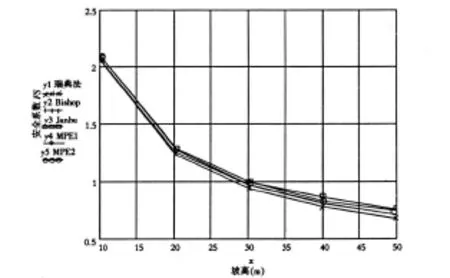
图6 不同坡高下的计算误差比较
2.4 不同坡比对计算结果的影响
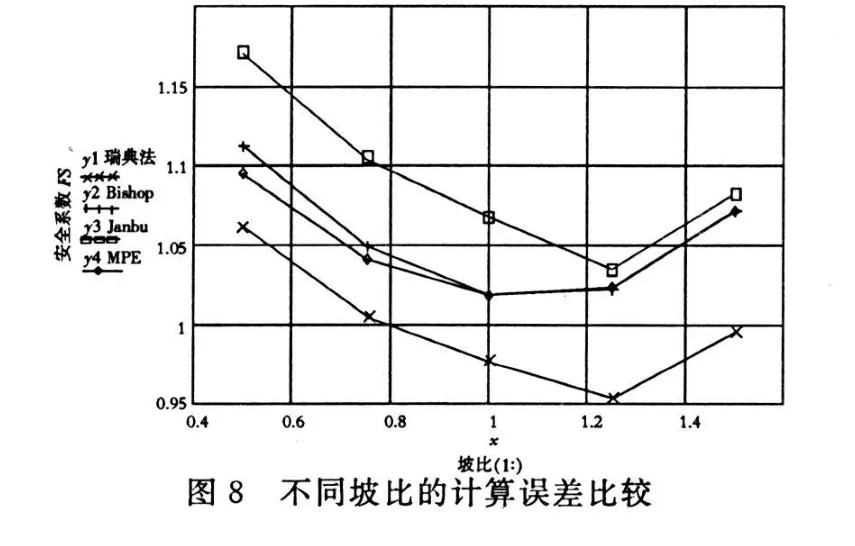
为分析坡比对最小势能法的安全系数的影响,采用图7所示的坡体,坡高30 m,内聚力 c=40 kPa,容重 γ=20.5 kNm3,内摩擦角 φ=15°,边坡控制点坐标:A(10,10),C(66,40),滑弧半径51.8413 m,圆心点O(18.6532,61.1140).四种不同坡比下极限平衡法和最小势能方法得到的安全系数结果如表5和图8所示.
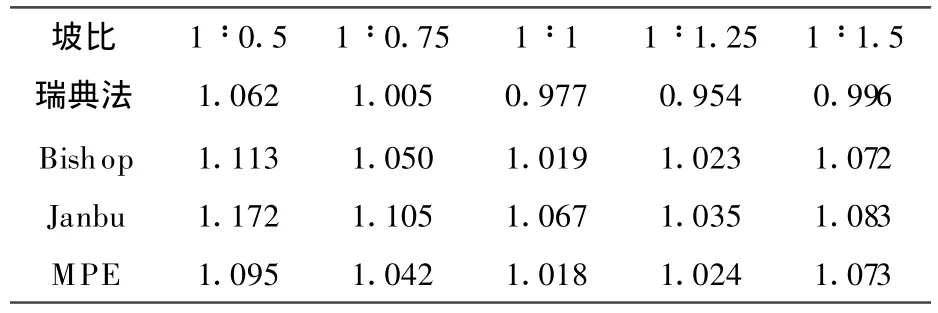
表5 不同坡比的计算结果
3 结 语

通过不同内聚力、不同内摩擦角、不同坡高、不同坡比情况下的算例分析,边坡稳定分析的最小势能方法与极限平衡法(包括瑞典法、Bishop法和Janbu法)的安全系数结果误差在3%之内.对比研究表明,最小势能方法和极限平衡法的计算结果比较接近,且结果也比较稳定,是一种比较可靠的边坡稳定分析方法.证明该法结果可靠度高,具有一定的工程实用价值[4,5].
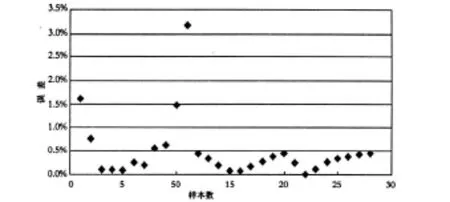
图9 最小势能法和Bishop法计算结果误差分析
[1]陈祖煜.土质边坡稳定分析[M]:原理◦方法◦程序.北京:中国水利水电出版社,2003.
[2]Mauldon.M.and Ureta,J.(1994)Stability of Rock Wedges with M ultiple Sliding Surfaces,Association of Geologists Annual Meeting,Williamsburg.
[3]李 铀,陆 洋,等.锚杆(索)加固边坡的最小势能稳定分析方法研究[J].岩土力学,2008,29(9):2331-2333.
[4]陆 洋,李 铀.最小势能二维边坡稳定分析方法的研究与应用[J].山西建筑,2005,31(21):114-115.
[5]陆 洋,李 铀.边坡平面破坏稳定分析的最小势能方法[J].工程建设与设计,2006,10:55-58.
——《势能》

