渗流自由面数值模拟方法比较

蒋胜银，李连侠，廖华胜，杨 华，邹 俊

（1.四川大学水力学及山区河流开发保护国家重点实验室，成都 610065；2.珠江水利科学研究院，广州 510611）

渗流自由面数值模拟方法比较

蒋胜银1，李连侠1，廖华胜1，杨 华1，邹 俊2

（1.四川大学水力学及山区河流开发保护国家重点实验室，成都 610065；2.珠江水利科学研究院，广州 510611）

结合最新提出的自由面适应网格法，与现行的2种固定网格法即变单元渗透系数法和初流量法进行数值模拟比较，以探讨各种方法在自由面渗流计算中的优缺点及其应用情况。试探性地选取3种固定网格方法进行系统的比较，即在精度、迭代步数、网格敏感度、初设自由面敏感性上进行多方位比较，分析各方法的灵活性、鲁棒性、数值稳定性、计算效率和可靠性。结果表明，在同一网格系统下，自由面适应网格法较其它2种方法具有计算速度快、精度较高等优点，其迭代步数和结果精度对初设自由面和网格密度敏感度均较其它2种方法低。

渗流自由面；数值模拟；固定网格方法；自由面适应网格方法

1 概 述

由于与水相联系，很多水工建筑物都有渗流问题。渗流会影响建筑物的受力情况以及结构物的材料性质等，所以，渗流关乎水工建筑物的安全性和可靠性。尤其在各类挡水建筑物中，例如：拦河坝、深基坑围堰、闸坝等。如果不能有效应对渗流，则可能发生建筑物滑动、土体渗透破坏、渗漏水量过大等问题。

国内外以往渗流研究的内容一般是过流体中浸润线的几何位置，过流体的水头场、水力坡降场和流速分布，渗流量等。以这些信息为基础，进行渗流的整体或局部渗流稳定性分析、质量的评估等。

渗流计算的数值模拟方法按网格性质的不同还分为变网格法、固定网格法和无网格法。本文探讨的主要是固定网格法。固定网格法即在计算中保持网格不变，采用扩大的渗流区域和固定边界（通常是全部区域和边界）来求解各种各样的渗流问题。自Neuman于1973年提出用不变网格分析带有自由面渗流问题的Galerkin方法［1］以来，出现了多种固定网格法，比较有影响的有Desai（1976）［2］稳定渗流计算的剩余流量法，并于1983年推广到非稳定渗流计算；Bathe（1979）［3］的单元渗透矩阵调整法；张有天［4］（1988）的初流量法。另外还有变分不等式法［5］、结点虚流量法［6］、虚单元法［7］、稳定渗流计算的截止负压法［8］、高斯点法［9］、变单元渗透系数法［10］等。

本文结合最新提出的自由面适应网格法［11］，与现行的几种固定网格法如变单元渗透系数法和初流量法进行数值模拟比较，以探讨各种方法在自由面渗流计算中的优缺点及其应用情况。

2 常见渗流自由面模拟方法

在数学范畴，自由面渗流和无自由面渗流的数学模型基本是一样的，但是无自由面渗流没有自由面边界和逸出边界，在数值模拟时，是一个线性问题，求解方便。反之，自由面渗流则因为自由面位置也为求解变量之一，对其求解则成为非线性问题，使得渗流计算变得复杂和困难。通常用迭代逼近的方法来求其近似解。具有自由面三维渗流问题的数学模型可用下式表示：

式中，K为渗透系数张量；H＝H（x，y，z，t）为水头；Ω为渗流计算区域；ΩH为源（汇）项；SS为储水率；t0为计算初始时刻，H0（x，y，z）为t0时刻Ω域的水头分布；Γ1为第1类（给定水头）边界，H1（x，y，z，t）为Γ1上的水头分布；Γ2为第2类（给定流量）边界；n2为Γ2的法向方向；q（x，y，z，t）为Γ2上的流量分布；Γ3为第3类边界，即渗流自由面边界；ε为Γ3上的补给强度；μ为给水度。

针对这一问题，为求解浸润面提出了诸多方法。本文主要针对渗流数值模拟方法中的固定网格法进行讨论。对于固定网格法而言，一般分为3类：第1类是弱化渗流自由面以上区域的影响，比如变单元渗透系数法、丢单元法；第2类是补偿流量的方法，比如剩余流量法、初流量法；第3类是自由面适应网格方法。为对比这3类方法的优劣，本文选取了3种方法：变单元渗透系数法、初流量法、自由面适应网格法进行比较。

2.1 变单元渗透系数法

为求解渗流自由面边界的变单元渗透系数法，具体做法如下：

（1）在上游水位与下游水位之间先估计出初始自由面的区域。

（2）对全区域进行网格划分，在预估的初始自由面域内将网格划分得很密。

（3）自由面上结点的水头等于其位置势，将自由面之上的所有结点进行标识并判断处于自由面上的所有单元。

（4）把位于自由面上单元的渗透系数改为一个很小的数。由于自由面之上的单元在第2次以后的迭代计算过程中，不需要参与计算，为了让自由面之上的单元对以后的计算不产生影响，方便编程序，所以把自由面以上的单元在迭代过程中都乘以一个很小的数，比如为10×10－3，足以在计算过程中把自由面以上的单元渗流结果忽略，不再考虑自由面以上单元对渗流的影响。

（5）进行下一次求解，将本次求出的结点势与上一次求出的结点势比较，当渗流域内结点均满足收敛条件时，渗流场中所有满足｜H－Z｜≤ε2的结点的连线即为自由面。

2.2 初流量法

初流量法是在达西定律中增加一初流量项q0i，通过对初流量值的调整，将一系列非线性分析化为线性分析。若以整个区域为考察对象（包括非饱和区），可将达西定律改写为

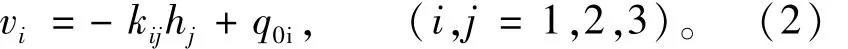
该式采用了张量记法，kijhj为介质渗透张量；q0i表示初流量值。

在计算中，通过第一步迭代的结果找出自由面以上单元和包含自由面的单元，通过单元高斯点的水头与高程的关系，判断是否计算初流量。形成了新的Q项（等效结点流量列阵）。解矩阵方程，通过这次的结果计算高斯点的流量，又形成新的Q项，迭代计算，直到满足收敛条件。

初流量法有3种收敛标准：①结点初流量的绝对值不超过某一允许量；②计算出的自由面稳定，若干次迭代后h＜z的高斯点数不变；③饱和区结点水头增量不超过某一允许量。本文选用的是后2个收敛标准。

2.3 自由面适应网格方法［11］

渗流计算中浸润线计算一般迭代过程可描述如下：

（2）求解渗流场，求出渗流自由面上的水头分布；

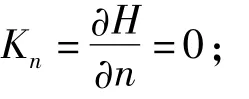
（4）重复第（2）和第（3）步，直到第n＋1和n次迭代所求出的水头Hn＋1和Hn的相对误差值在精度要求范围内；

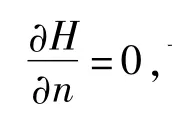
与其他方法不同，自由面适应网格法在浸润线（自由面）的调整过程中，不需要将网格变形，而是将浸润线按其所在位置，近似映射到最近的在既定网格系统中求解，其中的映射既可以是简单的零阶映射，也可是高阶映射，它最大限度地利用了浸润线上H＝z的边界条件特性。其具体方法如下（见图1）：图中a，b，c，d，e，f为其与纵向网格线的交点，abcdef为计算过程中可能的浸润线中间结果。对于浸润线上每一分段，按照距离节点位置最近原则把该段映射到计算节点上，如ab段就被映射到节点A1，A2，B上，依此类推，计算浸润线abcdef最后就按该原则被映射在固定网格系统中的A1A2BC1C2DE1E2F，该折线被称为映射浸润线，实现了自由面适应网格的过程。设｜A1a｜表示节点A1到点a的距离，｜Bb｜表示节点B到点b的距离，依此类推，则如果｜A1a｜，｜A2a｜，｜Bb｜，｜Cc｜，｜Dd｜，｜E1e｜，｜E2e｜，｜Ff｜的最小值满足精度要求，即计算浸润线和映射浸润线足够接近，就认为迭代收敛，否则进行下一点的迭代，直至收敛为止。

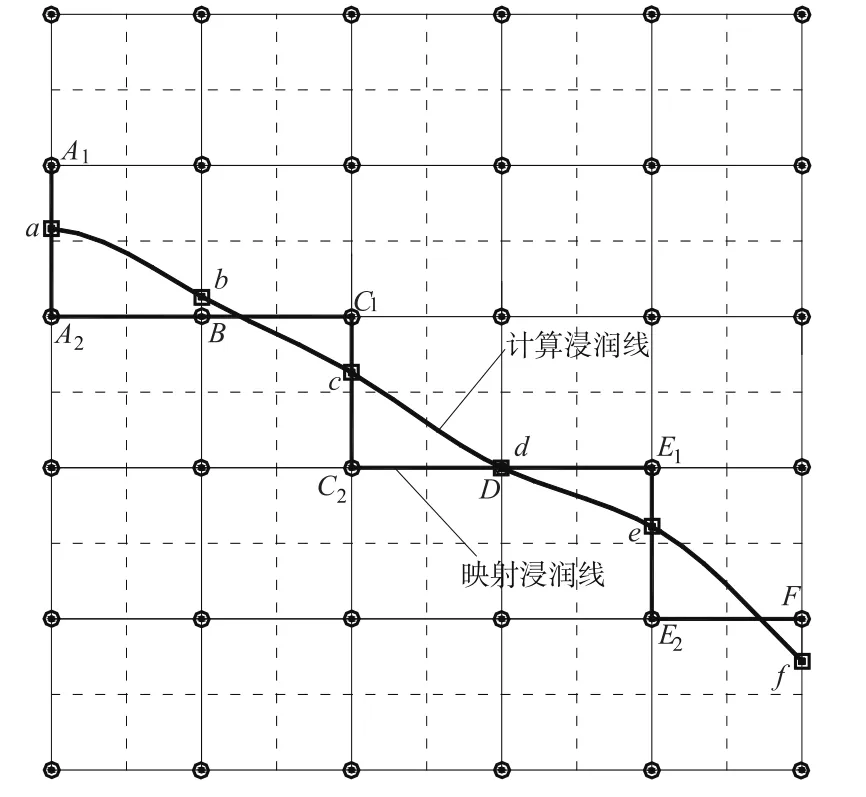
图1 自由面适应网格方法实现原理示意图Fig.1 Principle of adaptive grid for free surface

3 对比算例及比较参数拟定

3.1 对比算例及计算工况

梯形坝渗流是工程中常见的渗流现象，比如用于挡水的土石坝和基坑开挖的围堰堰体等建筑物其体型均属梯形坝。均匀介质的梯形坝的自由面渗流是有理论解的，通过这个理论解与3种模拟方法结果进行比较，可以进一步说明问题和发现问题。

选取的梯形坝体型如图2，上游坡面边坡系数m1＝3，下游坡面边坡系数为m2＝2。上游水位H1＝15 m，下游水位H2＝4 m。该梯形坝模型属于水平不透水层上均质坝。上游液体将通过边界AB渗入坝体，在坝内形成自由表面（浸润面）AC，C点称为逸出点，ABDC区域为渗流区。

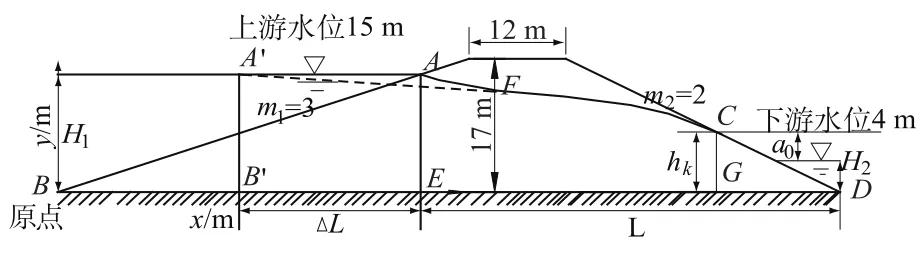
图2 梯形坝模型及自由面理论计算示意图Fig.2 Trapezoidal dam model and theoretical solution of free surface

上述问题浸润曲线的解析式［12］为

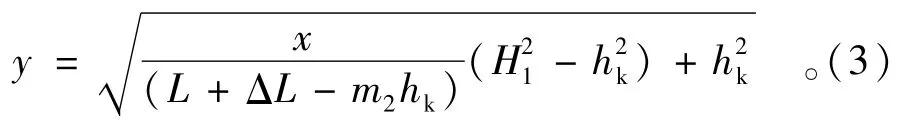
其中逸出点水深hk由（4）、（5）两式联立求解得出。（3）至（6）式中符号参见图2。

上游渗流段A′B′GC所通过的单宽渗流量：

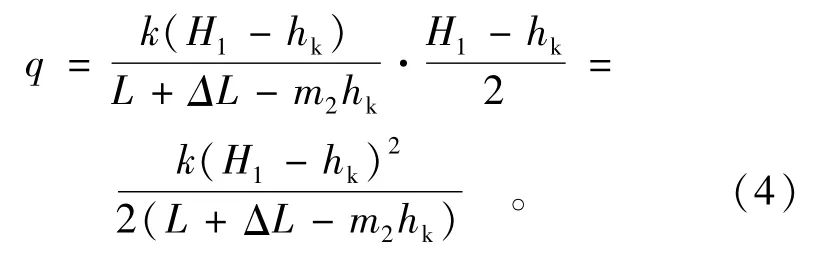
通过下游出渗段CGD的单宽渗流量为

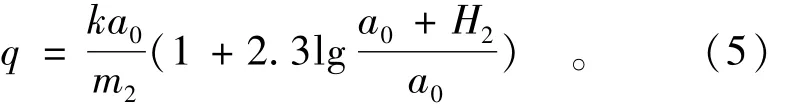
等效的矩形体的宽度ΔL由下式确定：

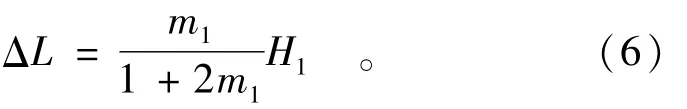
假定一系列的x值，由（3）式可得到相应的y值，从而描绘出梯形坝渗流浸润线如图3。表1给出该自由面解析解几个典型位置的解。

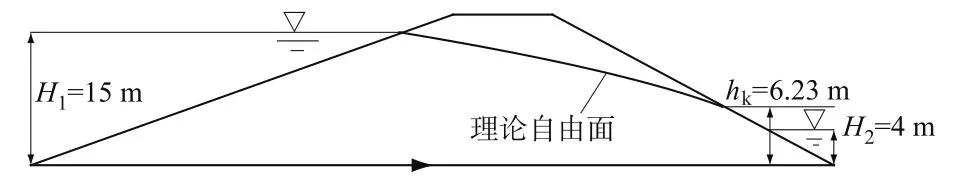
图3 梯形坝理论自由面示意图Fig.3 Theoreticalwater free surface of trapezoidal dam

表1 梯形坝自由面理论解Table 1 Theoretical solution of water free surface of trapezoidal dam

求得该梯形坝的理论解后，用3种数值模拟方法进行相应计算，并与上述理论解进行计算精度、初设自由面敏感度、网格敏感度和CPU时间的比较。计算工况分为2种网格和3种初设自由面，其计算工况见表2。

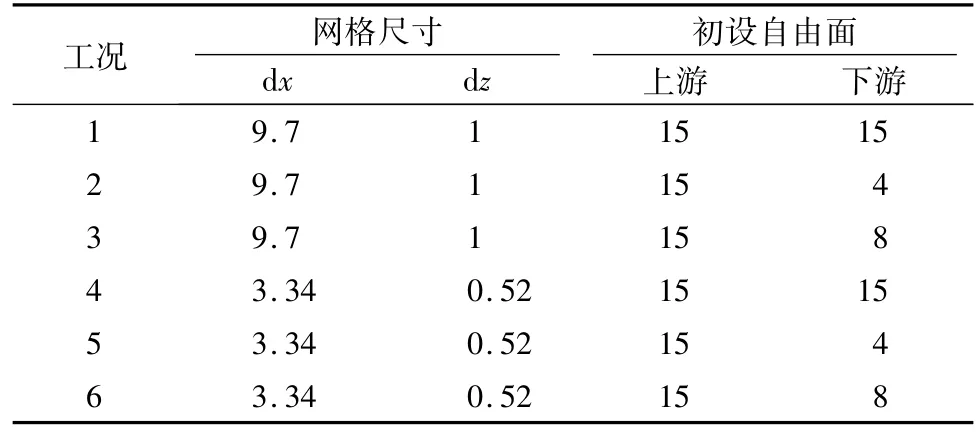
表2 计算工况Table 2 Com putational cases m

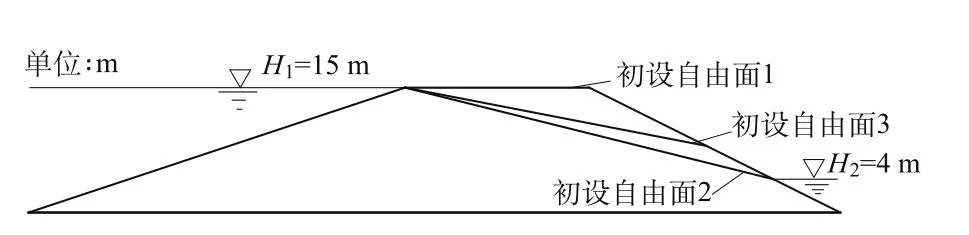
图4 初设自由面示意Fig.4 Initial free surface

初设自由面均为直线，其分布见图4。取值如下：初设自由面1，上游15m，下游15m；初设自由面2，上游15m，下游4m；初设自由面3，上游15m，下游8 m。

3.2 比较参数拟定

为分析相应方法的灵活性、鲁棒性、数值稳定性、计算效率和可靠性，针对以上选定方法和算例，拟定以下几个参数进行量化比较：①计算结果精确度；②初设自由面敏感度；③网格变化敏感度；④计算的CPU时间。

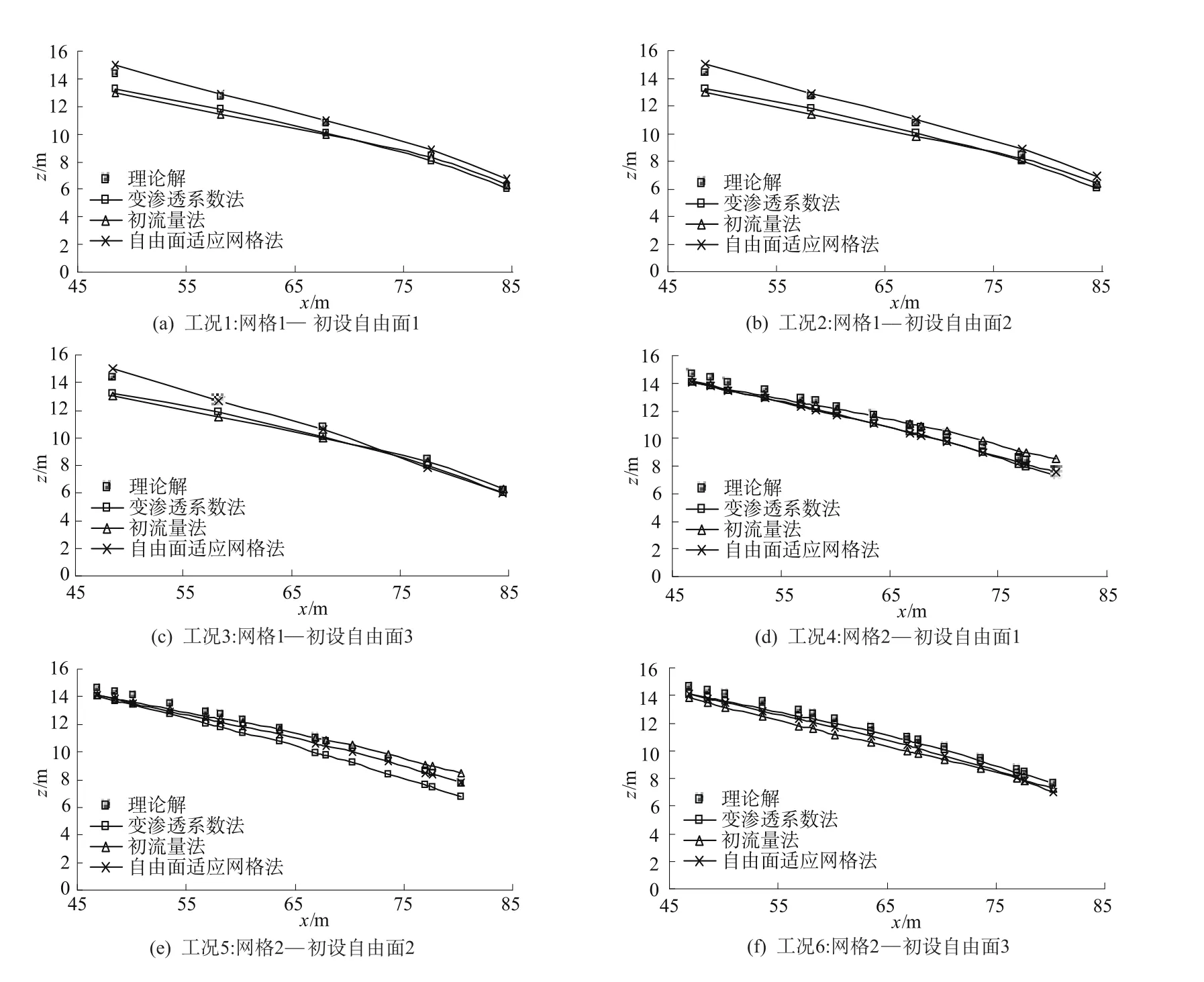
图5 不同工况下3种方法的计算结果精度对比Fig.5 Comparison of calculation accuracy of threemethods in different cases

4 模拟结果分析及比较

4.1 结果精度

3种模拟方法的计算结果精度对比见图5。一共6个不同的工况。3种方法结果与理论解的偏差程度进行对比，可看出它们求解准确性的相对差异。

可见，在同一工况下自由面适应网格法的结果总体较为稳定；初流量法的求解结果偏大，变渗透系数法结果一般。

4.2 初设自由面敏感度

对初设自由面敏感度的对比见图6。每种方法用3种初设自由面下的结果，计算各点数值的标准差。每种方法得到3种初设自由面下的3组标准差后，与其他的方法进行比较。

由图可见，这个算例的初设自由面敏感度三者大致相当。

4.3 网格敏感度

对网格敏感度的对比见图7，采用计算结果的标准差进行量化比较。

由图可见，自由面适应网格法的标准差最小（个别点较大），变渗透系数法次之，初流量法最大。这说明，自由面适应网格法和变渗透系数法的网格敏感度较小，具有较好的适应性和鲁棒性，并且自由面适应网格法对于尺寸较粗的网格也能得到较精确的结果，初流量法表现一般。

4.4 CPU时间

同种工况下CPU时间对比见表3。同种初设自由面下，当网格数目较少时，自由面适应网格法和变渗透系数法用时明显少于初流量法；且随着网格数目的增加，自由面适应网格法的用时增加速率远小于其它2种方法，CPU时间远小于其它2种方法，且网格数越多这种优势越明显。可见自由面适应网格法计算效率更高，更适用于大区域和复杂渗流问题的计算。

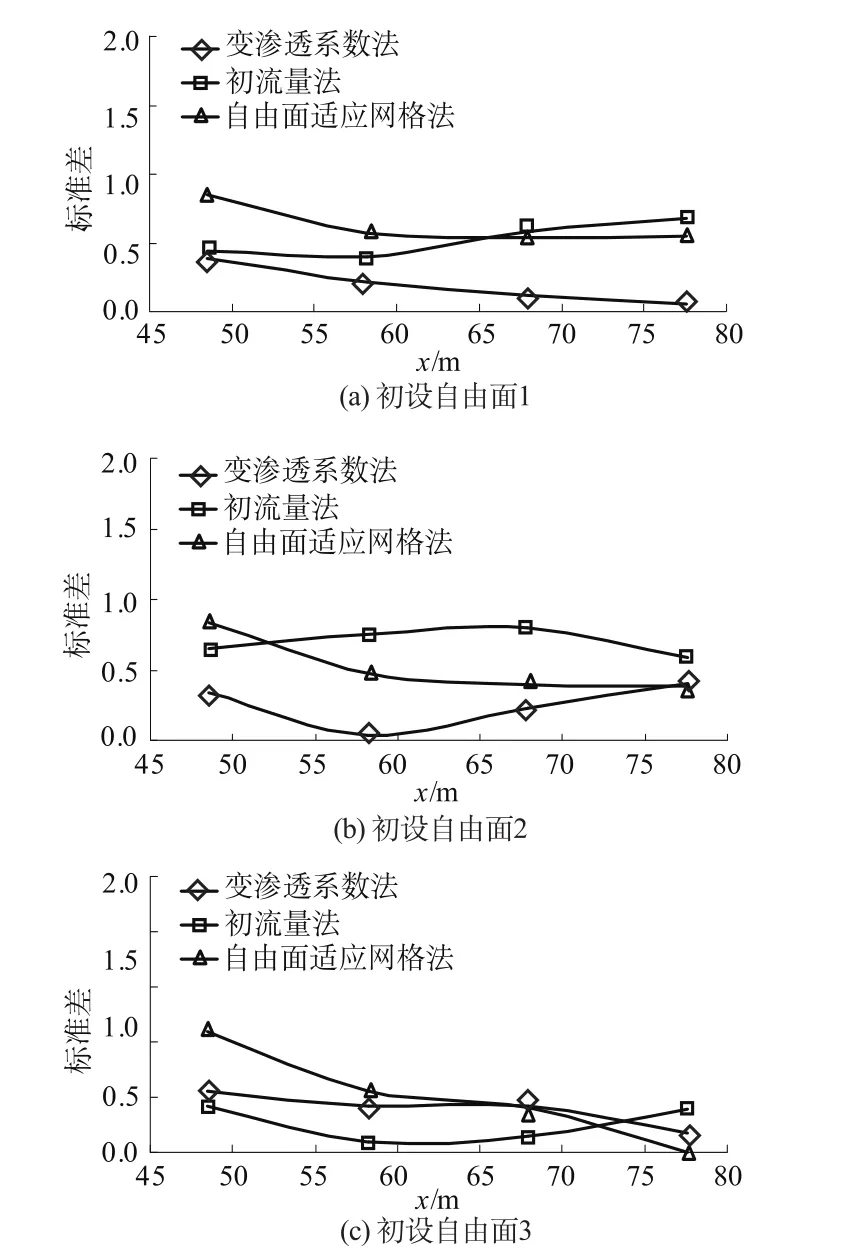
图6 不同初设自由面下3种方法计算结果的标准差Fig.6 Standard deviation of the results of three methods w ith different initial free surfaces

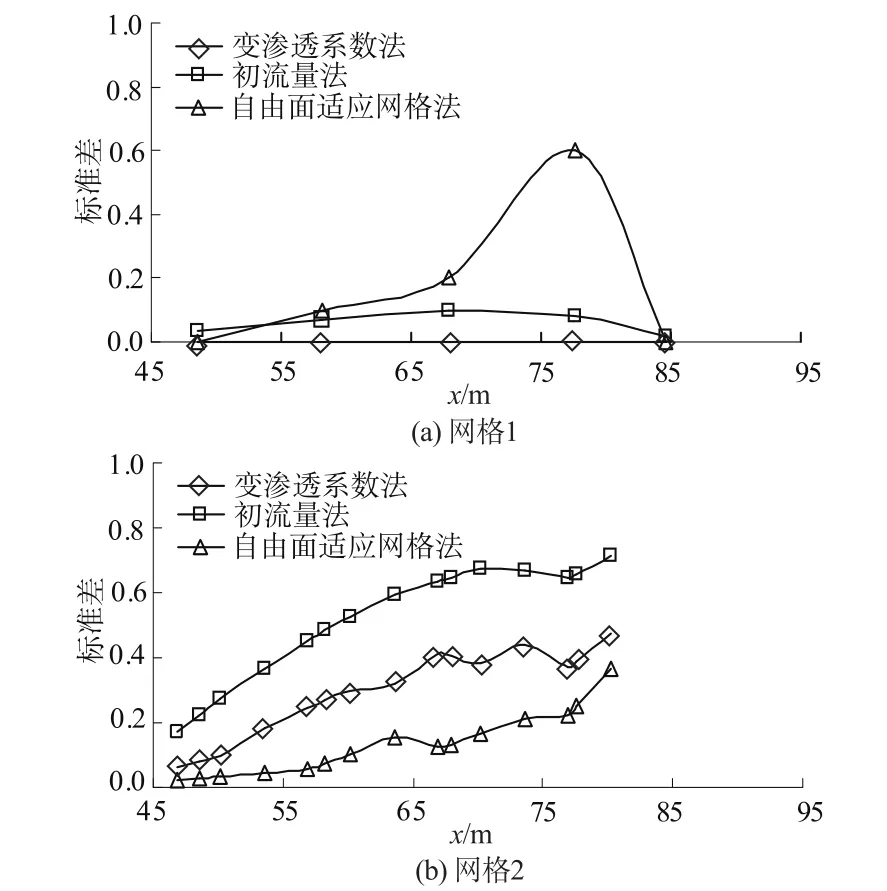
图7 不同网格下3种方法计算结果的标准差Fig.7 Standard deviation of the results of threemethods in different grids

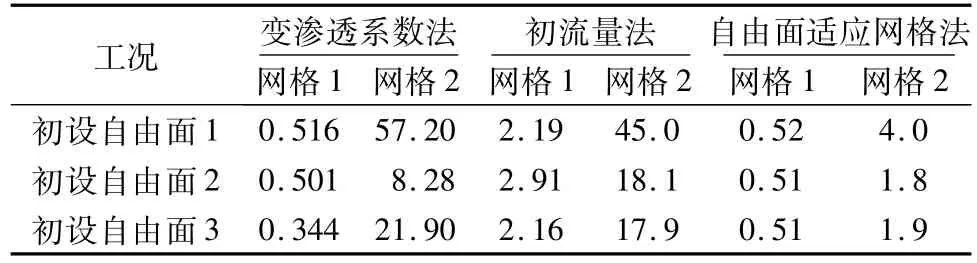
表3 网格1和网格2情况下3种初设自由面计算时间Table 3 The calculation time of three differentmethods w ith three initial free surfaces in grid 1 and grid 2 s

综上所述，3种方法的综合对比见表4，可看出自由面适应网格法综合能力优于其他2种方法：在大型计算时，变渗透系数的时间花费太大，小型计算时其效果较好；初流量法的计算指标居中。

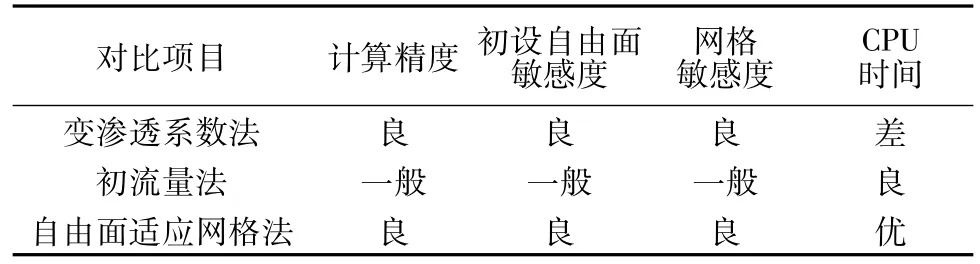
表4 3种方法综合对比Table 4 Com prehensive com parison of threemethods

5 结 论

本文选取了3种计算渗流浸润线固定网格方法，并拟定了方法间用于比较的参数：灵活性、鲁棒性、数值稳定性、计算效率及可靠性等。比较结果表明：

（1）自由面适应网格方法和变渗透系数法一样，具有良好的可靠性和计算精度。

（2）初设自由面对自由面适应网格方法影响较小，该方法具有较好的适应性和鲁棒性；初流量法受初设自由面的影响相对较大，变渗透系数法居于二者之间。

（3）初流量法和变渗透系数法迭代步数受网格疏密影响较大，随着网格数的增加而递增；而自由面适应网格法的计算结果受网格数目的影响很小，随着网格数的递增，迭代步数没有发生剧增，说明自由面适应网格方法具有良好的数值稳定性，在大区域和复杂渗流计算中具有良好的应用前景。

（4）自由面适应网格法进行自由面调整时，方法简单，除了映射计算，没有涉及过多的额外计算，而且该方法收敛较快，其CPU时间没有因为网格数目的增大而有数量级的增大，与其他方法相比优势明显，说明自由面适应网格方法具有良好的计算效率，更适用于大区域和复杂渗流计算中。

［1］ NEUMAN S P.Saturated-Unsaturated Seepage by Finite Elements［J］.Journal of Hydraulic Division，ASCE，1973，99（12）：2233－2250.

［2］ DESAIC S.Finite Element Residual Shemes for Unconfined Flow［J］.International Journal for Numerical Methods in Engineering，1976，10（6）：1415－1418.

［3］ BATHE K J.Finite Element Free Surface Seepage Analy-sisWithout Mesh Iteration［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1979，3（1）：13－22.

［4］ 张有天，陈 平，王 镭.有自由面渗流分析的初流量法［J］.水利学报，1988，（8）：18.（ZHANG You-tian，CHEN Ping，WANG Lei.Initial Flow Method for Seepage Analysiswith Free Surface［J］.Journal of Hydraulic Engineering，1988，（8）：18.（in Chinese））

［5］ BAIOCCHI C，COMINCIOLI V，MAGENES E，et al.Free Boundary Problems in the Theory of Fluid Flow Through Porous Media：Existence and Uniqueness Theoremes［J］.Annali Di Matematica Pura ed Applicata，1973，97（4）：1－82.

［6］ 速宝玉，朱岳明.不变网格确定渗流自由面的节点虚流量法［J］.河海大学学报，1991，19（5）：113－117.（SU Bao-yu，ZHU Yue-ming.Nodal Virtual Discharge Method for Seepage Problems with Free Surface on Fixed Grids［J］.Journal of Hohai University，1991，19（5）：113－117.（in Chinese））

［7］ 吴梦喜，张学勤.有自由面渗流分析的虚单元法［J］.水利学报，1994，（8）：64－71.（WU Meng-xi，ZHANG Xue-qin.Imaginary Element Method for Numerical Analysis of Seepagewith Free Surface［J］.Journal of Hydraulic Engineering，1994，（8）：64－67.（in Chinese））

［8］ 速宝玉，沈振中，赵 坚.用变分不等式理论求解渗流问题的截止负压法［J］.水利学报，1996，（3）：22－29，35.（SU Bao-yu，SHEN Zhen-zhong，ZHAO Jian.The Cut-off Negative Pressure Method for Soling Filtration Problems Based on the Theory of Variational Inequalities［J］.Journal of Hydraulic Engineering，1996，（3）：22－29，35.（in Chinese））

［9］ 王贤能，黄润秋.有自由面渗流分析的高斯点法［J］.水文地质工程地质，1997，（6）：1－4.（WANG Xianneng，HUANG Run-qiu.Gavss PointMethod for Seepage Analysis with Free Surface［J］.Hydrogeology and Engineering Geology，1997，（6）：1－4.（in Chinese））

［10］党发宁，王晓章，郑忠安，等.有自由面渗流分析的变单元渗透系数法［J］.西北水力发电，2004，（1）：1－3.（DANG Fa-ning，WANG Xiao-zhang，ZHENG Zhongan，et al.Variable Element Seepage Coefficient Method for Seepage Numerical Analysis of Seepagewith Free Surface［J］.Journal of Northwest Hydroelectric Power，2004，（1）：1－3.（in Chinese））

［11］李连侠，廖华胜，刘 达，等.渗流计算中求解浸润线的自由面适应网格方法［J］.四川大学学报（工程科学版），2006，（5）：76－81.（LI Lian-xia，LIAO Hua-sheng LIU Da，etal.A Method ofWater Free Surface Adapting Grid System to Simulate Phreatic Surface in Seepage Flow［J］.Journal of Sichuan University（Engineering Science Edition），2006，（5）：76－81.（in Chinese））

［12］吴持恭.水力学（下册）［M］.北京：高等教育出版社，2008：234－238.（WU Chi-gong.Hydraulics（Volume Two）［M］.Beijing：Higher Education Press，2008：234－238.（in Chinese） ）

（编辑：王 慰）

Comparison of Numerical Approaches of Simulating Seepage Flow w ith Free Surface

JIANG Sheng-yin1，LILian-xia1，LIAO Hua-sheng1，YANG Hua1，ZOU Jun2
（1.State Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Sichuan 610065，China；2.Pearl River Hydraulics Research Institute，Guangzhou 510611，China）

The fixed grid methods can be classified into initial flow method，variable seepage coefficientmethod，variational inequalitymethod，node imaginary flow method，imaginary elementsmethod and the water free surface adaptive grid method which was put forward recently.Each method has its advantages and disadvantages.To ultimately guide us to choose propermethods when processing the practical seepage problems in large scale，it is of great value to evaluate their applicability including flexibility，robustness，numerical stability，computational efficiency and reliability by comparing the accuracy，iterative steps，grid sensitivity，and initial free surface sensitivity of three different fixed grid methods.The results show that the water free surface adaptive grid method is of higher computing efficiency and accuracy than the other twomethods in the same grid system.The initiative steps are less，and the accuracy of computing results is less sensitive to the initial free surface and grid density than the other two methods.

free surface of seepage flow；numerical simulation；fixed grid methods；method of water free surface adaptive grid

TV139.1

A

1001－5485（2011）07－0037－06

2010-08-30

教育部博士点新教师基金（20090181120013），四川大学青年基金（0030614132002）

蒋胜银（1986-），男，四川成都人，硕士研究生，主要从事水工水力学方面的研究，（电话）15528330512（电子信箱）scujsy＠163.com。

李连侠（1978-），男，河南南阳人，副教授，主要从事水工水力学方面的研究，（电话）13308021514（电子信箱）lianxiali＠yahoo.com.cn。