浅谈RC桥式振荡电路的教学新思路
郭 姣,刘艳良
(海军大连舰艇学院基础部,辽宁大连 116018)
正弦波振荡电路是“模拟电子技术”课程中的重要内容之一。在现有的教材中,通常采取的讲法是:从负反馈放大电路产生自激振荡的原理和条件出发,推导出正弦波振荡电路的起振条件、振荡条件及其组成要素(即放大电路、正反馈网络和选频网络),进而分析RC桥式正弦波振荡电路的组成与工作原理[1,2]。这样的编排尽管条理清晰,但初学者在有限的课时内正确理解这些内容十分困难。
笔者针对正弦波振荡电路教学内容的特点,提出了一种新的教学思路,旨在突破教学难点。实践表明,这样讲解符合初学者的认知规律,更利于学生理解和掌握这部分教学内容。
1 RC桥式振荡电路的教学思路
RC振荡电路内容属于原理性教学,目的是要让学生理解振荡器的振荡原理和振荡条件。我们在教学过程中,通过设置目标,引导学生利用已学过的知识和方法进行分析。该部分内容采用探究型教学模式,即演示导入→设疑激趣→启思解疑的三步式教学模式,如图1所示。
2 RC桥式振荡电路教学内容的导入
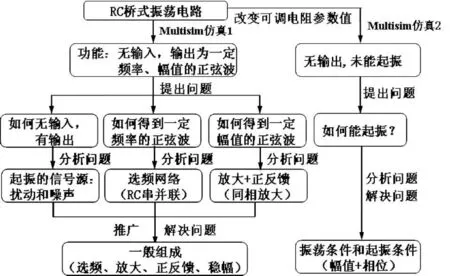
图1 RC桥式振荡器的教学思路示意图
在传统的RC桥式振荡电路讲法中,由负反馈放大电路产生自激振荡的原理导入,进而得到正弦波振荡电路的起振条件、振荡条件及其组成要素,会使学生觉得比较抽象。笔者在教学中采取了以下做法。
首先,将RC桥式振荡的电路图展示给学生,观察其组成有两部分:一是同相放大电路,一是RC串并联网络。抛出的问题是,从结构上看,该电路没有输入,会有输出吗?如果有输出,其波形会如何?然后,在如图2所示的Multisim环境中连接好电路,在示波器中观察接通电源后的输出波形,如图3示。
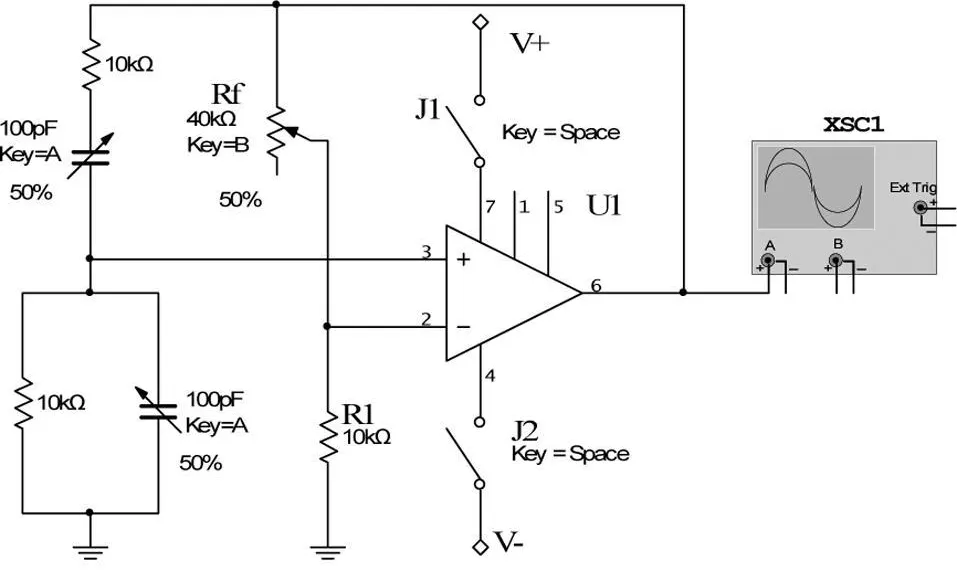
图2 RC桥式振荡电路的Multisim仿真图
由此,学生得到该电路的功能,即不需要外加激励,就能产生一定频率和幅值的正弦波信号。进而,学生会提出疑问:该电路为何具有如此功能,其输出波形为何具有幅度从小增大和进而稳定的特点呢?实践表明,借助仿真电路及其波形,可化抽象为具体,为学生进一步理解正弦波振荡电路的功能与原理打好铺垫。
3 RC桥式振荡电路教学内容的展开
RC桥式振荡电路的组成及工作原理是教学的难点。为了帮助学生解决理解过程中的困难,笔者在教学中采取了将难点分散的做法,也即把一个大问题分解为如下三个小问题。
(1)无输入为何有输出?
为了解决该问题,我们引导学生进行分析,根据能量守恒定律,输出的能量应当由电源提供。在刚接通电源的一瞬间,电路内部一些器件上就发生了微弱的电压电流变化,我们把这一现象称为电源接通扰动,仿真后的波形如图4所示。这种扰动信号和电路中的噪声都可看作是电路的信号源,因而该电路并非无中生有。
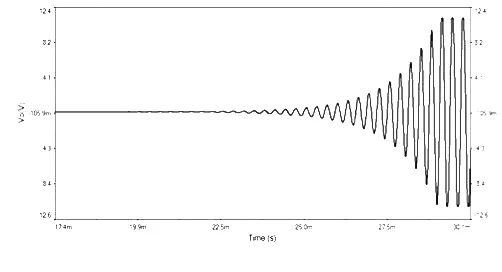
图3 RC桥式振荡电路仿真波形
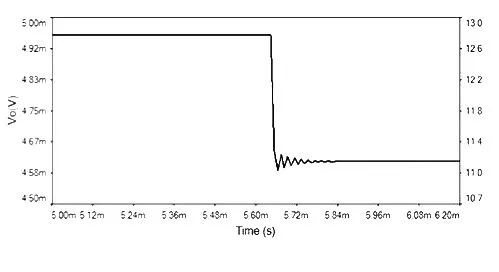
图4 电源接通时的扰动波形
扰动和噪声信号的幅度很微弱,需进行处理。学生容易想到,要得到所需幅值的正弦波,需要放大电路。在RC桥式振荡器中,可实现放大的是同相放大电路,其放大倍数为1+Rf/R1。由于信号太小,还需将放大后的信号送回输入端反复放大,即电路中需要引入反馈,显然是正反馈。在RC桥式振荡器中,可承担反馈的是RC串并联网络。于是,该电路的输出幅度从小到大实现了起振。
(2)如何输出一定幅值的正弦波?
学生进而会提出疑问,该电路的幅值会无限制地增大吗?根据运放器件的特点可知,当信号幅度增大到一定程度后,就会使得运放进入非线性区工作,从而限制了幅度的增加,达到了稳定幅度的目的,最终输出一定的幅值的正弦波。通常,振荡电路也可引入其他稳幅环节。
(3)如何得到一定频率的正弦波?
扰动和噪声信号还具有频率范围广的特点,要从多个频率的信号中只选取出一个频率的信号,显然需要选频网络。在RC桥式振荡电路中,可实现选频的是RC串并联电路。此时我们可引导学生考察RC串并联网络的频率特性,更易使学生接受。通过推导RC串并联网络输出与输入之比随频率变化的特性,可得其幅频特性曲线和相频特性曲线,如图5所示。
可见,RC串并联网络的频率响应特性曲线具有明显的峰值,该网络具有选频作用。该网络在 ω=ω0=1/RC处,其输出输入之比取最大值1/3,输出输入相位差为0。
针对这一结论,我们可调节电容C的大小对该电路进行Multisim仿真。在示波器中可以观察电容C改变时,发现电路的波形输出频率发生了变化,如图6所示。通过这一仿真实验,可使学生对RC串并联网络的选频特性具有更深刻的理解。
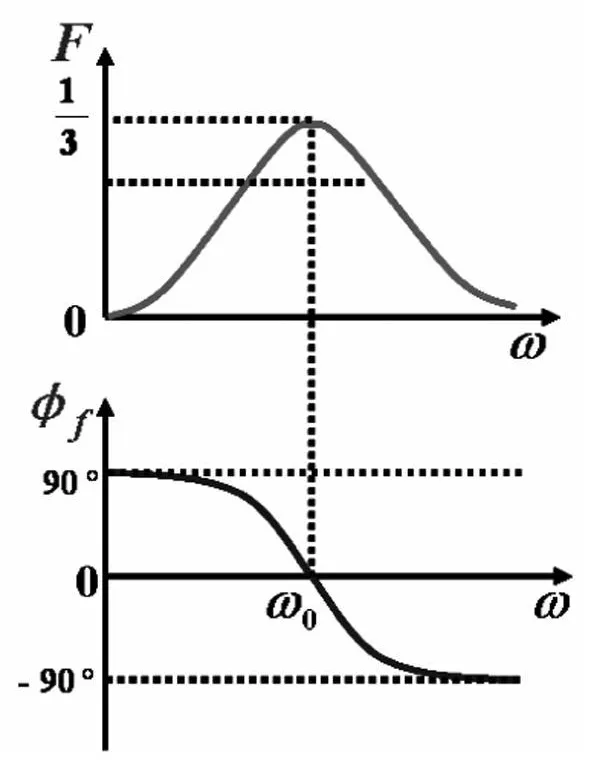
图5 RC网络的频率特性
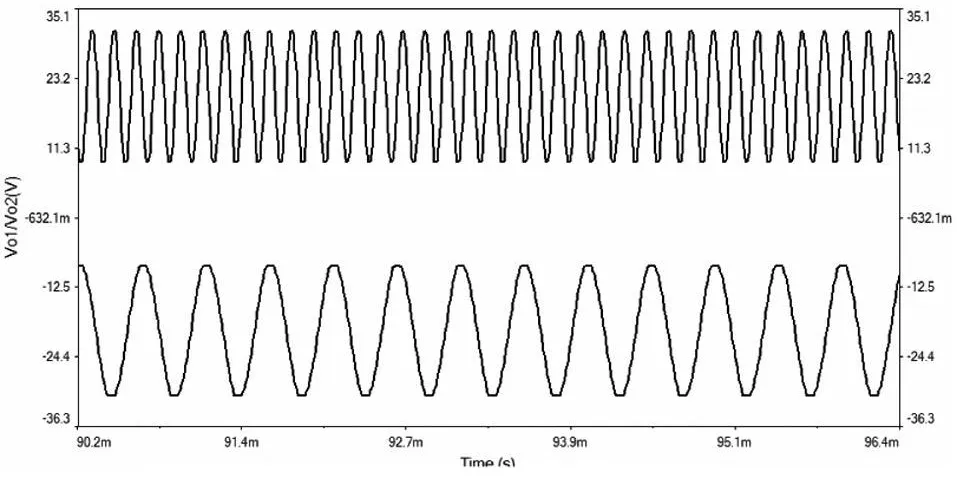
图6 电容C改变时的电路仿真波形
通过解决以上三个问题,学生可得到这样的结论:正弦波振荡电路的振荡过程,是由扰动和噪声信号中选取一定频率的正弦波信号进行放大且稳定在一定幅度,因而电路需由选频网络、放大电路、正反馈网络和稳幅电路组成。通常,选频网络可以充当反馈网络的作用,稳幅电路也可包含在放大电路当中,所以整个振荡器由两大部分组成:放大A与反馈F,框图如图7所示。
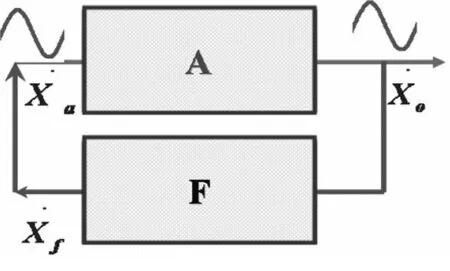
图7 正弦波振荡器的组成框图
4 RC桥式振荡电路教学内容的深入
经过以上讨论,学生已基本理解RC桥式正弦波振荡电路的功能和工作原理,以及正弦波振荡电路的组成要素,我们可以进一步引导学生深入思考:若具备了正弦波振荡电路的组成要素,就一定能输出一定频率和幅值的正弦波吗?
若将图1所示振荡电路中的可调电阻Rf变小至19kΨ,输出波形会发生什么样的变化?利用Multisim软件对参数改变后的电路进行仿真,在示波器中观察接通电源后的输出波形,如图8所示。
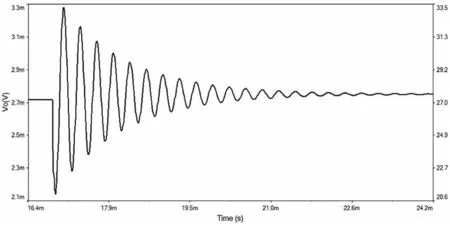
图8 电阻Rf参数改变后的仿真波形
仿真后发现参数改变后未能起振,原因是什么?我们借助该问题,调动学生分析问题和解决问题的积极性,可引导学生推导出正弦波振荡电路能够振荡的条件。
由图7可知,要想维持振荡需输出波形的后一时刻与前一时刻相同,需要后一时刻与前一时刻的输入波形相同,即·Xf=·Xa,因而·Xf/·Xa=1,可写为
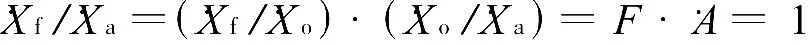
由此可推导出维持振荡的条件为 ·A ·f=1。其中,振幅平衡条件 AF=1,相位平衡条件+=2nπ。学生容易进一步得到起振条件为AF>1和+=。
现在,我们再来分析RC桥式正弦波振荡电路。由于选频网络的F=1/3。为了满足起振条件,需要求A>3。为满足稳幅条件,需使得A=3。即同相放大电路中,选择参数Rf≥2R1。至此,我们已经引导学生解决了正弦波振荡电路起振条件和维持振荡条件的问题。
最后,可将正弦波振荡电路的振荡条件与负反馈放大电路的自激振荡条件相比较,学生就更易发现,两者之间的区别仅为正负反馈相位相差π。
5 结语
笔者在正弦波振荡电路的教学中,将电路的起振稳幅过程进行仿真,将电路的工作原理进行难点分解,将电路的振荡条件引导学生推导,使学生加深了对振荡电路的理解和掌握,收到了较好的教学效果。
[1] 康华光主编,电子技术基础(第5版)[M].北京:高等教育出版社,2007,434~441
[2] 吴友宇主编,模拟电子技术基础[M].北京:清华大学出版社,2009,292~298

