架空导线覆冰实验及模拟
顾小松 ,王汉青,刘和云
(1.中南大学 能源科学与工程学院,湖南 长沙,410083;2.长沙理工大学 能源与动力工程学院,湖南 长沙,410076;3. 湖南人文科技学院 计算机科学系,湖南 娄底,417000)
架空导线覆冰将引起线路过载、不同期或者不均匀脱冰、导线舞动等一系列现象,造成线路断线、倒杆(塔)、闪络、磨损、断电等事故。对导线覆冰机理的研究既是输电线路荷载设计的理论依据,又是环境热物理研究的新课题,具有重要的理论和实际意义[1−4]。覆冰观测即在覆冰区建立结冰观测哨所,安装各种测试设备,系统地长期地记录有关数据,然后对所观测的数据进行统计分析,绘制出地理区域结冰分布图,用以指导导线线路设计和运行管理[5]。然而,有些研究者认为对导线覆冰进行模拟没有必要,但覆冰观测是一项费时、费钱、艰苦而又没有当前效益、需要长期、系统记录的工作,且并不能保证送电线路的安全。例如,1998年美国和加拿大发生的暴风雪对输电线路及其附属设备造成了巨大的破坏,而在那些进行了长期覆冰观测的区域同样损失惨重[6]。导线的覆冰过程取决于它所处的复杂大气和地理条件,覆冰量随时间变化较大,它不可能满足某一种仅仅从测量的数据就能得出的某种概率分布,而且,在世界上有许多地区是无法获得结冰数据。与对覆冰进行直接观测相比,覆冰模拟的优点有:(1)随着气象预测技术及设备的发展,现在很容易获得不同地点各个时刻的天气参数,可以被用来作为模型的输入以获得导线的覆冰量。(2)合理的理论覆冰模型可以为导线结构强度设计人员提供极端条件下的覆冰情况,而这种极端天气条件以前没有碰到过,因而没有经验数据可供设计者参考。(3)防冰和除冰系统的开发也需要对覆冰过程进行模拟,对于某些构件,例如飞机、直升飞机、风力发电机叶片,即便是少量覆冰也可能会改变自身空气动力学特性从而造成危害。在此,本文作者在一个小型开式冰风洞中对导线覆冰过程进行测试,通过改变风洞中气流的风速、温度、液态水含量来观测不同气象条件下导线覆冰的特点,测出在不同工况下覆冰量和冰的密度。对覆冰的热平衡模型进行了改进,编写覆冰计算程序,将模拟值与实验值进行比较和误差分析,证明此模型是合理的。
1 实验方法
图1所示为实验系统示意图。冰风洞设置在1个冷库改造成的低温环境室中,2台使用氟利昂的压缩冷凝机组(JZ−35)为环境室提供冷源,环境室内安装有墙排管蒸发器,最低温度可以达到−20 ℃,室内靠墙设置环形风道,形成覆冰实验风洞,试验段的尺寸为0.35 m×0.35 m。水通过对流换热管冷却进入雾化喷嘴(利用压缩空气使水雾化),液滴随气流在风洞中流动, 在风道的实验段上下平行布置3根导线,长度为0.2 m。环境室内的温度(ta)由制冷机房自动控制系统调节,室内空气湿度由超声波加湿器进行调节,风速(v)由变频风机调节,风速调节范围0~20 m/s,液态水含量(w)通过喷嘴的水流量调节,液滴平均体积直径(dm)可由喷嘴的特性曲线获得。用皮托管测量管道内的风速,镍铬−康铜热电偶测量气流温度,细导线测量空气中的液态水含量,冰密度的测量采用浸没排液法,把覆冰浸入同温度的四氯化碳中得出冰的体积,在电子秤上称出冰的质量,即可以得到冰的密度。
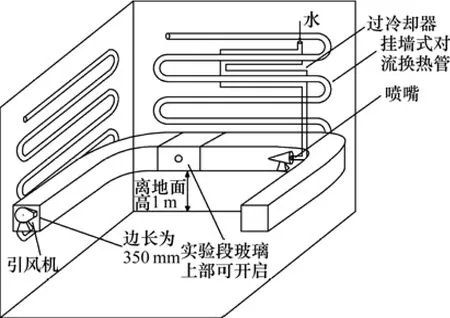
图1 实验系统图Fig.1 Experimental system chart
2 实验结果及分析
实验圆导线直径为12.36 mm,根据喷嘴的特性曲线,取液滴的平均体积直径dm=25 μm。选取2个典型工况:工况 1,v=10 m/s,t= −10 ℃,w=0.12 g/m3;工况2,v=6 m/s,t= −2 ℃,w=0.08 g/m3。工况1和 2的1~3 h覆冰见图2和图3,1~6 h密度变化见图4。

图2 工况1导线覆冰图Fig.2 Icing on conductors of working condition 1

图3 工况2导线覆冰图Fig.3 Icing on conductors of working condition 2
2.1 温度对覆冰的影响
在实验中发现:当气流温度较低时(−10 ℃),覆冰呈干增长,液滴在离开喷嘴进入风道后,在风道中就已经开始冻结,覆冰类型为雾凇,松散而且与导线间黏合力小;当气温上升为−4 ℃时,覆冰开始呈现质地较硬的混合凇,覆冰与导线间黏附力较大;当温度继续上升到−2 ℃时,覆冰呈现透明、质地坚硬的雨凇,黏附力和密度都大大增加,这时候覆冰对导线危害最大。从传热的角度分析,产生这一现象的原因为:气温较低时,被导线捕获液滴冻结放出的潜热能够通过对流散热散发到周围的空气中,被捕获的液滴全部冻结,冰表面的温度始终能够保持在0 ℃以下,随着气温的升高,覆冰导线对流散热小于液滴所能释放出的潜热时,被捕获的液滴不能全部冻结,这个时候冰表面温度维持在0 ℃。
图4所示为工况1和2导线覆冰密度变化。由图4可知:气温为−10 ℃时,工况1冰的密度随着时间的增加逐渐降低,但减小的幅度不大,平均值约为250 kg/m3;当温度升高到−2 ℃时,工况2冰的密度急剧升高,平均值达到860 kg/m3。由此可见,气温对冰密度具有重要影响。

图4 工况1和2导线覆冰密度变化Fig.4 Ice density variation of working conditions 1 and 2
2.2 液态水含量对覆冰的影响
空气的液态水含量w是指单位体积云体中,含有液态水滴的总质量。w主要受到温度的影响,当温度很低的时候,云里面的水蒸气容易凝华为冰晶或者液态水滴冻结成冰晶,导致w降低;当云的温度渐渐升高,空气中水蒸气含量增加,w也增加。一般说来,当温度略低于冰点的时候,w随着高度的增加而增大。对于给定的温度和水滴直径,w的增加可使覆冰类型从雾凇向雨凇转化。实验中液态水含量可以通过调节喷嘴的喷液流量实现,当w较大时,过冷水滴更易碰撞在物面并沿着物面向后流动,覆冰的类型受温度的影响较小,覆冰基本都是湿增长,覆冰类型多为雨凇或混合凇。当液态水含量显著增加时,导线的覆冰量增加也较大。
2.3 风速对覆冰的影响
图5所示为导线覆冰量随风速的变化。由图5可见:当温度为−9 ℃,喷嘴用水量为0.295 kg/h时,随着风速在2~6 m/s间变化,导线的覆冰量会增加。随着风速的增加,导线对水的收集率(收集系数)增加,因此,捕获的过冷水滴量会增加。风速为2,4和6 m/s时对应的冰平均密度分别为246,247和249 kg/m3,变化较小,因此,风速对冰密度的影响可以忽略不计。
2.4 过冷水滴粒径对覆冰的影响
空气中水滴直径尺寸不是单一的,而是呈一定的分布,覆冰研究中将过冷水滴的平均体积直径(dm)定义为将总水量等分成两半的临界尺寸,即认为直径大于dm的大水滴的总体积与直径小于dm的小水滴的总体积相等。实验中液滴粒径是由喷嘴气源(压缩空气,由空气压缩机提供)以及水源的压力以及流量决定的,确定这些量后,由喷管的特性曲线可查得dm,因此,本实验中dm实际上不是一个直接测量的量,实验中发现在其他条件不变的情况下,增加液滴的dm,导线的覆冰量会增加,但当dm增加到一定值时,导线的覆冰量变化就很少了,这是因为刚开始dm的增加会使得导线对液滴的收集系数(<1)增加,如果dm继续增加,收集系数将维持在1。
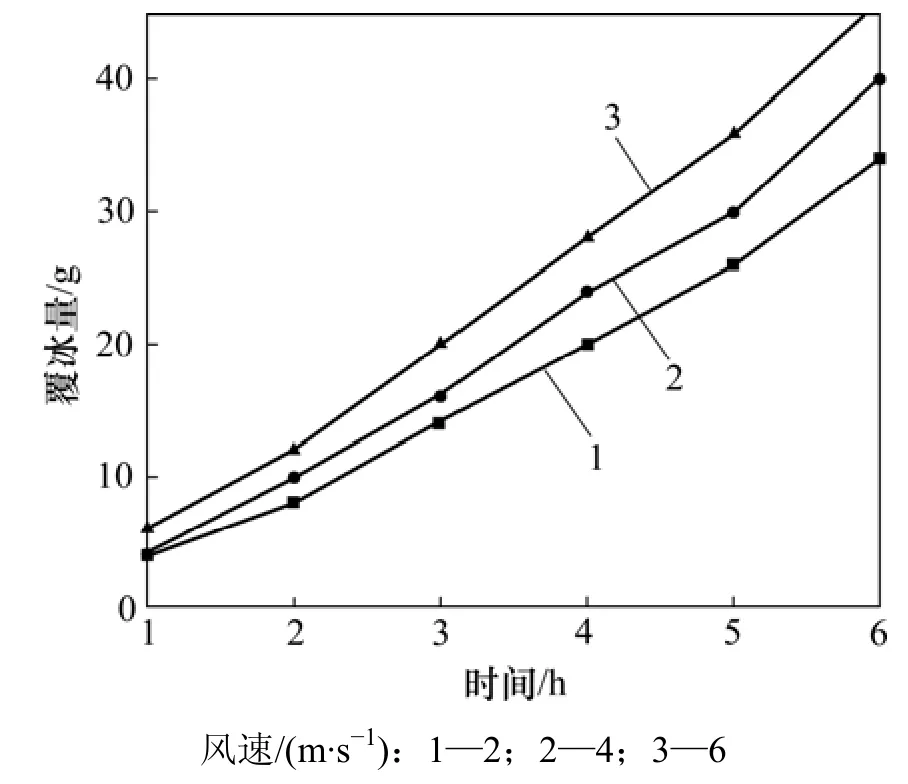
图5 导线覆冰量随风速的变化Fig.5 Ice loads variation with air velocity
3 覆冰模型的改进
3.1 热平衡模型
Makkonen等[7−12]对覆冰导线表面传热过程进行分析,建立了如下热平衡方程。
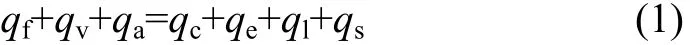
式中:qf为过冷却水滴冻结时释放的潜热;qv空气对导线气动加热热流;qa为将冰从0 ℃冷却到覆冰表面温度所释放的热量;qc为冰表面与气流之间的对流、导热所散失的热量;qe为覆冰表面蒸发或升华带走的热量;ql为加热水滴使之温度升高到0 ℃时所需的热量;qs为冰面辐射产生的热流(忽略)。
迎风面单位表面积冰的增长速度称为结冰强度(kg/(m2·h)),其计算式如下:

其中:E为收集系数,它表示实际的表面撞击水量与最大可能(整个迎风面)收集水量的比;n为冻结系数,表示导线收集到的水冻结成冰的比例。当n<1时,冰为湿增长,也就是说,总体上有部分水从覆冰表面流失而没有冻结;当n=1时,所有被导线捕获的过冷水滴都冻结,覆冰过程为干增长。Makkonen[7−8]给出了各项热流量的计算式,根据热平衡方程(1)可确定冻结系数的大小,再根据方程(2),就可求出导线上的覆冰量或者覆冰当量直径。
在热平衡模型中有3项热流量是主要的,其中过冷却水滴冻结时释放的潜热及冰表面的蒸发热损失这两项均与收集系数E有关,另一项则是冰表面与空气之间的对流换热系数,它取决于努谢尔特数Nu及雷诺数Re的准则式。Makkonen[7−8]在热平衡模型中选用了一个E的经验关系式,将过冷却水滴直径分成了3个区段,关系式的使用范围局限于导线直径为10~200 mm,风速为1~30 m/s的范围内。选何种Nu与Re关联式会影响到对流换热量计算的准确性,从而影响模型的预测结果,Makkonen[7−8]所采用的经验关联式Nu=0.032Re0.85并没有经过实验验证。
3.2 改进的模型
刘和云等[13−14]通过对收集系数进行量纲分析,并在冰风洞中对收集系数进行测试,通过对数据的分析处理,得出了E的准则关联式为:

其中:De=D/d;dm为过冷水滴的平均体积直径;D为导线的当量直径。
同时在冰风洞中对3种类型的覆冰导线(雾凇、雨凇和混合淞)的对流换热特性进行实验研究[13−14],根据实验数据得出如下准则关联式:

温度验证范围为−20~0 ℃,Re范围为 1×104~1×106。
改进后的模型用式(3)和(4)代替热平衡模型中收集系数E以及对流换热准则式。由上面的分析可知:覆冰相关量(覆冰量、当量直径和收集系数)是时变的,计算较为复杂,需要编程求解,程序的输入参数为气流速度v、 温度t、大气中过冷水滴的平均体积直径dm、液态水含量w和覆冰时间τ,输出为冰密度、冰负荷和冰的当量直径。
3.3 模拟值与实验值比较及误差分析
工况1和工况2的模拟与实验结果比较见图6和图7。可知:两者模拟值间的最大误差率为12%,产生误差可能的原因有:
(1)模拟值针对的是导线被均匀大气自由来流横掠过,由于壁面的影响实验风洞中气流不均匀,导致同一根导线不同部分的收集系数以及附近空气含水量可能不一致。从图3可以看出:靠近两边壁面的导线由于受到不均匀气流的影响,结冰不规则。
(2)w受到喷嘴位置、压力、速度的影响,所以,很难预先控制它达到某一数值,只能先设定好风速、温度后进行测量,实验中用的是一根很细的导线测出某一时间内的覆冰量,然后计算出w。
(3)液滴的直径受喷嘴汽液两相的压力影响,喷出来的液滴为一个滴谱而不是单一某个直径液滴。
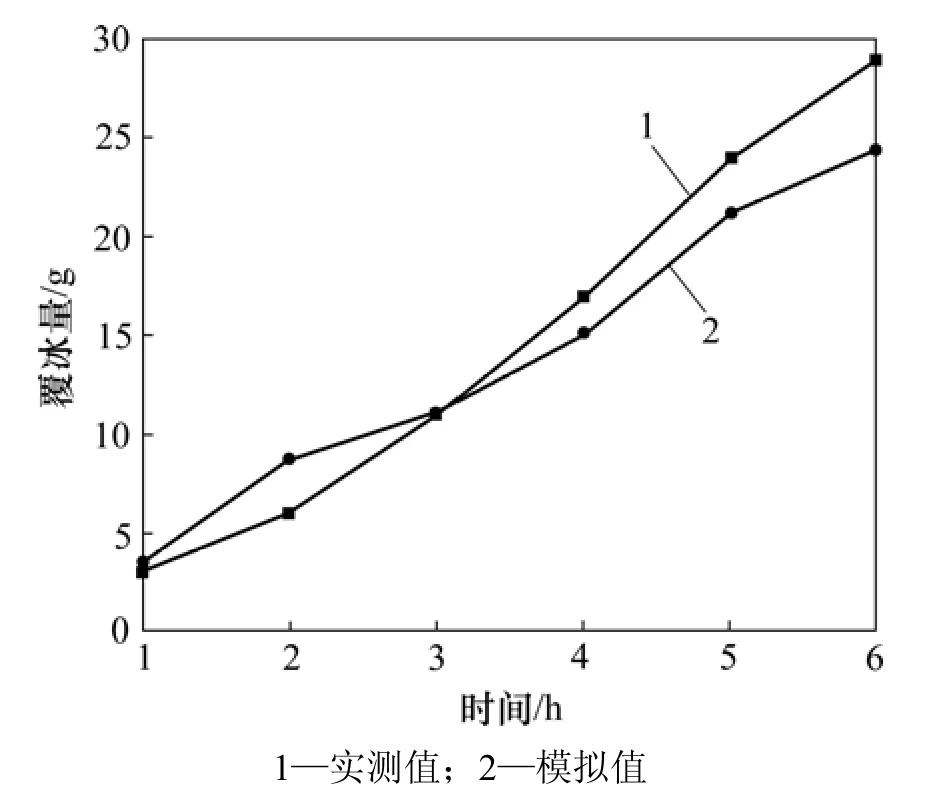
图6 工况1实验与模拟覆冰量比较Fig.6 Comparison ice loads of experiment and simulation for working condition 1

图7 工况2实验与模拟覆冰量比较Fig.7 Comparison ice loads of experiment and simulation for working condition 2
4 结论
(1)当空气中液态水含量较低时,导线上的覆冰在温度较低(≤−5 ℃)时为干增长(雾凇),随着温度的升高,逐渐转化为湿增长(雨凇),覆冰密度大大增加。当空气中液态水含量较高时(例如下冻雨时),覆冰一开始就为湿增长。
(2)在其他条件不变的情况下,风速的增加会导致覆冰量的增加,冰密度也会增加但幅度不大,过冷水滴平均直径的增加会使覆冰量增加。
(3)覆冰热平衡模型中关键参数为收集系数以及空气与覆冰导线间的对流换热系数,应由实验来确定计算这2个参数的准则关联式。
[1]Laforte J L, Allaire M A, Laflamme J.State-of-the-art on power line de-icing[J].Atmospheric Research, 1998, 46: 143−158.
[2]Zsolt P, Masoud F.Assessment of the current intensity for preventing ice accretion on overhead conductors[J].IEEE Transactions on Power Delivery, 2007, 22(1): 565−574.
[3]Maurice H, Christian L, Josee C.Combined models for glaze ice accretion and de-icing of current-carrying electrical conductors[J].IEEE Transactions on Power Delivery, 2005,20(2): 1611−1616.
[4]Zsolt P.Modeling and simulation of the icing process on a current-carrying conductor[D].Quebec: University of Quebec.CIGELE, 2006: 125−131.
[5]Thorsteins E, Ellasson A J.Ice load measurements in test spans in Iceland-statistical analysis of data[C]//Proceedings of the 8th International Workshop on Atmospheric Icing of Structures(IWAIS 1998).Reykjavik, 1998: 285−289.
[6]Mcclure G, Johns K C, Knoll F.Lessons from the ice storm of 1998: Improving the structural features of hydro-quebec’s power grid[C]//Proceedings of the 10th International Workshop on Atmospheric Icing of Structures.Brno, 1998: 380−385.
[7]Makkonen L.Models for the growth of rime, glaze, icicles and wet snow on structures[J].The Royal Society, 2000, 358:2913−2939.
[8]Makkonen L.Modeling of ice accretion on wires[J].Journal of Climate and Applied Meteorology, 1984, 23: 929−939.
[9]Makkonen L.Heat transfer and icing of a rough cylinder[J].Cold Regions Science and Technology, 1985, 10: 105−116.
[10]Makkonen L.Estimating intensity of atmospheric ice accretion on stationary structures[J].Journal of Applied Meteorology,1981, 20: 595−600.
[11]Personne P, Gayet J F.Ice accretion on wires and anti-icing induced by joule effect[J].Journal of Applied Meteorology, 1988,27(2): 101−114.
[12]Poots G.Ice and snow accretion on structures[M].England:Research Studies Press, 1996: 96−104.
[13]刘和云, 周迪, 付俊萍.导线雨凇覆冰预测简单模型的研究[J].中国电机工程学报, 2001, 21(4): 44−47.LIU He-yun, ZHOU Di, FU Jun-ping.A simple model for predicting glaze loads on wires[J].Proceedings of the CSEE,2001, 21(4): 44−47.
[14]刘和云.架空导线覆冰防冰的理论与应用[M].北京: 中国铁道出版社, 2001: 123−125.LIU He-yun.Theory and application of ice accretion and de-icing on overhead lines[M].Beijing: China Railway Press,2001: 123−125.

