基于小波变换的数字图像融合研究

徐进伟 李灿平

（成都理工大学信息科学与技术学院，四川 成都 610059）

1.引言

不同图像传感器获取的图像数据在几何、光谱、时间和空间分辨率等方面存在明显的局限性和差异性，所以仅仅利用一种图像数据难以满足实际需求。为了对观测目标有一个更全面、清晰、准确的理解和认识，人们迫切希望寻求一种综合利用各类图像数据的技术方法。与单源图像相比多源图像融合具有更多优势，这是因为多源图像具有冗余性，具有单源图像无法捕捉的信息，即多源图像之间具有互补性，因此多源图像融合能够从多个视点和多个时段获取信息，扩大时空的传感范围，提高观测的准确性和清晰度。如何把从各种不同传感器得到的图像融合起来，以便更充分地利用这些信息成为图像处理领域重要的研究课题之一。近年来,小波变换作为一种变换域信号处理方法,得到了非常迅速的发展,在信号分析、图像处理、地震勘探和非线性科学等诸多领域得到了广泛的运用。小波变换用于信号与图像融合是小波分析应用的一个重要方面，它的特点是融合准确度高，融合效果好，融合后能保持信号与图像的总数据量不变，且在传递中可以抗干扰。

2.小波变换

小波变换已经广泛地应用到了图像处理的各个领域，如图像编码、图像压缩、图像降噪、图像增强、图像融合等。由于小波变换本身所具有的优点，使得小波在图像融合方面也具有广阔的应用前景。

2.1 小波变换理论

小波是由傅立叶变换发展起来的，那么首先来看小波函数的表示，ψ(x)L2(R),且ψ(x)满足允许条件：

从上式中可以看出ψ(x)一定是震荡形的函数，所以说这就是小波（Wavelet）这一名称的由来。

对ψ(x)进行伸缩、平移，就得到一簇函数：

上式中的a是伸缩系数，又称尺度因子。b为平移因子，ψa,b(x)称为由母函数ψ(x)生成的连续小波基函数。

上面介绍了连续小波变换，这种连续形式的小波一般适用于理论分析。但在实际应用中，特别是计算机图像处理方法的实施中，更为重要的是离散的形式，即对连续小波函数式中的参数a、b离散化。

2.2 小波多分辨率分析

小波变换就是沿着多分辨率这条线发展过来的，与时域分析一样，一个信号用一个二维空间表示，不过这里的纵轴是尺度而不是频率。变尺度是通过对基本小波膨胀和压缩而构成的一组基函数来实现的。基本小波ψ(x)∈L2(R)被伸缩为ψ)，（a>1时变宽，a<1时变窄)以构成一组基函数。在大尺度

a上，膨胀的基函数搜索大的特征，而对于较小的a，它们则寻找细节信息。

多分辨率分析的性质：

（1)致单调性： Vj⊂Vj-1,j∈Z

（3)伸缩规则性：f(t)∈Vj⇔f(2jt)∈V0

（4)平移不变性：f(t)＝Vj⇒f(t-2jk)∈Vj

（5)里兹基存在性：存在函数 ø∈V0使得{ø(t-n)}n∈Z构成V0的里兹基，即：

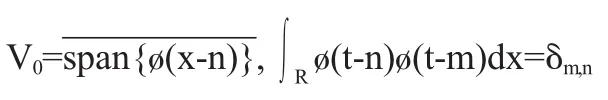
由多分辨率的定义可以看出，所有的闭子空间{Vj,j∈Z}都是由同一尺度的函数ø∈V0，伸缩后平移系列张成的尺度空间，称ø(t)为多分辨率分析的尺度函数。尺度函数ø(t)的傅里叶变换(ω)具有低通滤波的特性，小波函数ψ(x)的傅里叶变换(ω)具有高通滤波特性。这样利用尺度函数ø(t)和小波函数ψ(x)构造信号的低通滤波器和高通滤波器，可以对信号进行不同尺度下的分解。

3.基于小波变换的数字图像融合

图像融合的实质主要是一种信息的融合，要完成融合，最主要的是它融合的对象。一些彼此具有相关信息的图像，通过一些特定的规则来综合源图像的重要信息，从而得到一幅统一的图像或数据。

图像融合的算法大致可分为以下三个层次：像素级图像融合，特征级图像融合，决策级图像融合。像素级的图像融合是在严格的图像配准的条件下，对原始图像中相同的目标和背景以及相同级别的像素灰度进行的综合分析和处理。像素级图像融合能够使融合后的图像中的信息增加，相对于其它层次上的融合处理来说，在完全显示图像细节信息方面，像素级融合处理的效果是最好的。本文重点讨论像素级图像融合方法。图像融合的一般过程可由图1表示。

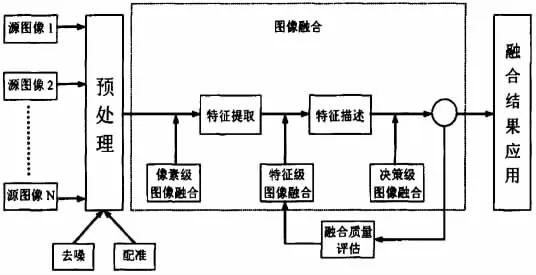
图1 图像融合流程

像素级图像融合方法大致分为三大类：简单的图像融合方法;基于塔形分解的图像融合方法;基于小波变换的图像融合方法。简单的图像融合方法一般是指直接在图像的像素灰度空间上进行融合处理。它不对参加融合的源图像做任何变换或分解，其算法简单、融合速度快、实时性好，可用于大多数的融合情况中，但是这种方法的图像融合效果一般是无法令人满意的，特别是在源图像彼此之间的灰度差异很大的情况下，这种方法就会出现明显的拼接痕迹。塔式分解的图像融合过程是在各个分解层上分别进行，这种结构能够突出原始图像中的重要特征和细节信息，并且融合后的效果较好；基于小波变换的图像融合算法是一种多尺度分解图像融合方法，由于小波分解具有非冗余的特性，图像经过小波分解后数据总量不会增大，而且小波重构不会损失原始图像中的信息。同时，小波分解具有良好的方向性，利用这一特性就可以针对人眼对不同方向的高频分量具有不同分辨率这一视觉特性分别进行融合，因此可以获得视觉效果更佳的融合图像。

4.试验与分析

4.1 实验所用的方法

（1）简单的图像融合方法-线性加权融合

线性加权融合就是对源图像进行加权平均作为融合结果。线性加权融合的一般形式可以用公式表示为：F(i,j)=ωAA(i,j)+ωB*B(i,j)

其中A(i,j),B(i,j),F(i,j)分别表示原图像A、B及融合图像F在点(i,j)处灰度值；ωA、ωB为加权系数，ωA+ωB=1，若 ωA=0.5，ωB=0.5，则为平均加权。

（2）基于塔式分解的图像融合

（3）基于小波变换的图像融合

4.2 实验效果及分析

工程中获得的全景图像实验：

（1）平硐右壁展开图的效果

图2 平硐右壁展开图效果

结果分析：

图2中(a)(b)(c)是一个平硐内壁右侧的连续的3幅图像展开图，采取竖向拼接融合，(a)图像在上面，(b)在(a)的后面，(c)在(b)的后面。在这三幅原图中可以看出来存在有重叠的区域，这样就可以利用我们上述的方法进行融合的操作。方法1的处理结果图中存在非常明显的拼接痕迹，特别是在图像的右侧；方法2的处理结果图的中拼接痕迹不明显了，但是拼接的部分变得模糊了，融合的效果相对也比较的柔和，过渡平和；方法3的处理结果图中，拼接融合的效果最好，基本上看不出拼接融合的痕迹，过渡非常自然，达到了我们要求的效果。

（2）平硐左壁展开图的效果

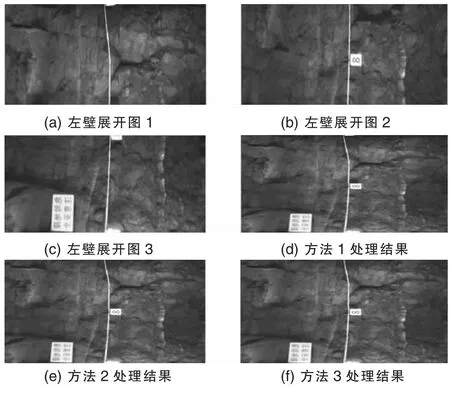
图3 平硐左壁展开图效果

结果分析：

图3中(a)(b)(c)是平硐内壁左壁的三幅连续的展开图，按(a)(b)(c)的顺序拼接融合。方法1处理结果中存在明显的拼接融合的痕迹，方法2处理结果图中的拼接融合的痕迹虽然不像方法1中的那么明显，但是可以看到存在一个过渡带，过渡带显得比较模糊，但是效果上面已经比较自然了。最后的方法3的处理结果图中，拼接融合的效果非常好，过渡自然，没有什么明显的拼接融合的痕迹。

5.结束语

通过以上平硐内壁的左壁、右壁展开图的试验可以看到，本文所讨论的基于小波变换的数字图像融合方法基本可以完美地再现原始情况的原貌。由此可以看出,小波变换与图像处理的结合将使信号、图像处理进入更高的层次。

[1]何东健.数字图像处理[M].西安：西安电子科技大学出版社,2003.

[2]张凤晶,程红,孙文邦.基于小波变换的图像融合方法研究[J].影像技术,2010,(06)：15-18.

[3]王爱玲等.MATLAB R2007图像处理技术与应用[M].北京：电子工业出版社,2007.

[4]周伟.MATLAB小波分析高级技术[M].西安：西安电子科技大学出版社,2006.

[5]阮秋琦,阮宇智等译.数字图像处理(第二版)[M].北京：电子工业出版社,2007.

[6]马令坤,张震强.图像拼接算法的研究[J].微计算机信息,2007,23(2/3)：303-305.