基于经验模式分解和1维谱的客车轴承故障诊断

陈晓军，杨江天

（1 郑州铁路局 郑州车辆段，河南新乡453000；2 北京交通大学 机械与电子控制工程学院，北京100044）

25型客车是我国主型铁路客车，设计要求连续运行5 000 km无检修。为了保证行车安全，必须有效排除轴承故障。当前，我国铁路客车广泛使用轴承温度报警系统，及时发现温度过高轴承，防止燃轴、切轴事故发生，取得了很好的效果。但滚动轴承从损伤出现到发热烧损的过程比较漫长，一般情况下轴承故障并不表现为明显的温度升高。为了提前发现轴承故障，现在普遍试验采用振动信号分析法实现轴承早期故障诊断。需要指出的是铁道车辆轴承振动信号复杂，噪声干扰来自各个频带［1］。滚动轴承冲击响应由一系列单边衰减振荡信号组成，轴承故障特征频率包含的能量非常少，故障诊断必须使用强有力的信号分析方法才能将故障信息突出出来［2－3］。有 关 研 究 表 明，1维谱能有效抑制高斯噪声，检测信号二次相位耦合［4］，提取滚动轴承故障特征［5］。但当信号受到多频带噪声干扰时，识别准确率下降。经验模式分解（Empirical Mode Decomposition，EMD）是HUANG［6］等人于1998年提出的新的信号处理方法，相当于一种滤波器簇［7］。本文提出了一种客车轴承检测分析方法：首先用EMD处理轴承振动信号，滤除干扰。再将滤波后的信号进行1维谱分析，提取

故障特征频率。该方法成功用于25型客车轴承故障检测，指导轴承维修。

1．1 定义

设有随机变量x（t），其三阶自相关定义为

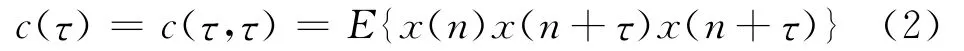
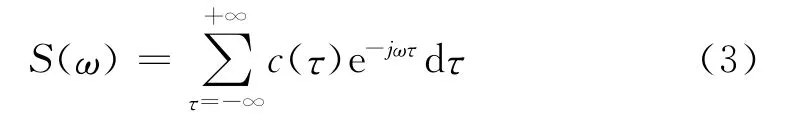
（2）检测二次相位耦合

机械系统发生故障时，系统行为相对于正常状态往往表现出较强的非线性，故障越严重，非线性就越强。最常见的非线性是两个谐波成分间相互关联作用，产生1个和频与1个差频频率成分，称为二次相位耦合。1维谱可以描述二次相位耦合，在1维谱上仅出现参与相位耦合的频率成分。

客车轴承典型故障形式是表面疲劳损伤。轴承出现这种故障后，在受载运转过程中，损伤点撞击与之相接触的其他元件表面而产生低频振动，称为轴承的“通过振动”。通过振动发生的频率称为故障特征频率，由轴转速，轴承几何尺寸及损伤的位置（内圈、外圈、滚动体、保持架）唯一确定。损伤点以故障特征频率反复撞击与之相接触的其他元件表面产生的宽带脉冲，作用于轴承及其支承结构，使损伤轴承振动的特征为冲击激励产生的减幅振荡。减幅振荡的上升沿是一个非常陡的脉冲，与元件表面和损伤点的冲击相对应。随后，能量被内部阻尼消耗，脉冲以近似指数包络线衰减。局部损伤滚动轴承振动信号包括故障特征频率的一簇谐波，它们的相位是相互关联的，即振动信号存在二次相位耦合。用1维谱提取信号相位耦合特征是滚动轴承故障诊断的有效方法［5］。

2 经验模式分解

与傅里叶分析不同，经验模式分解是直接、基于信号时域局部特征和自适应的信号分解。它可把复杂的信号分解成一系列固有模态函数分量（Intrinsic Mode Functions，IMF）。每个IMF为满足以下两个条件的信号：① 整个信号中过零点数与极点数相等或至多相差1；② 由局部极大值点确定的上包络线和由局部极小值点确定的下包络线的均值都为零，即信号关于时间轴局部对称。满足以上两个条件的基本模式分量被称为固有模态函数（IMF）。因为在按过零点定义的每一周期中，只包括一个基本模式的振荡，没有复杂的叠加波存在。

对任一实信号x（t）进行EMD的具体步骤为［6］

① 确定出x（t）上的所有极大值点和极小值点，将所有极大值点和极小值点分别用三次样条曲线连接起来，将这两条曲线分别作为x（t）的上、下包络线。计算出它们的平均值曲线m1（t），用x（t）减去m1（t）得

如果h1（t）不满足IMF的条件，需要把h1（t）作为原信号重复上面的步骤k次，直到找出第1阶IMF。记作

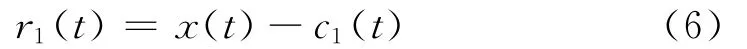
②从原信号中减去c1（t）得到第1阶剩余信号r1（t）为把r1（t）作为新的原信号，重复步骤①。对后面的rf（t）也进行同样的筛选，这样依次得到第2阶IMF、……、第n阶IMF和剩余信号。最终可得分解式即原始数据可表示为若干固有模态函数分量和一个残余项之和。

从上述分解过程（图3）可以看出：EMD先分解出高频信号，然后依次分解出次高频、低频信号，构成一滤波器组。频带宽度由信号本身的特点所决定。由于经验模式分解是自适应划分信号频带的，所以能够克服小波分解中频带二分所引起的缺乏灵活性的缺点，也不要求选择窄带滤波的中心频率及带宽等参数，降低了对分析人员的要求。因此，具有很好的实用价值。

3 诊断实例

试验车为一辆25K型车，209 HS转向架，轴箱轴承为NJ3266X1型圆柱滚子轴承。在各轴承上安装加速度传感器，随车运行采集轴承振动信号。选取车辆以120 km／h速度稳定运行的数据进行分析，对应车轴转速696 r／min。在此转速下，轴承故障特征频率为

图1为某轴承振动信号波形，采样频率5 k Hz。图中可见振动信号存在幅值较大的冲击成分和减幅振荡。但是这些振荡信号被噪声所掩盖，时域上反映不很明显，难以分析。

图2为对应的功率谱，在0～2 000 Hz整个频带内存在丰富的频率成分。由于线路、车辆结构和噪声等因素的作用，轴承振动信号很复杂，在功率谱上出现诸多频率成分，轴承故障特征频率不突出。

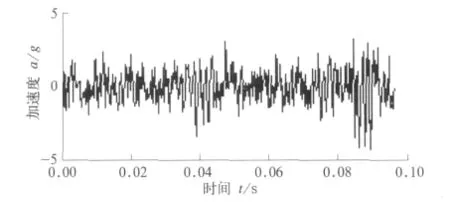
图1 客车轴承振动（加速度）

图2 客车轴承振动功率谱

图3为对轴承振动信号经验模式分解的结果，（a）图是各阶列固有模态函数分量，（b）图是对应的功率谱。c1是从原序列中分解出的幅值最小、频率最高的IMF分量，各IMF分量的幅值逐渐增大、频率逐渐降低，直到频率很低的c7和c8分量。观察EMD的分解过程可以发现EMD可以看作自适应滤波器组，各IMF分量是包含在原始信号中的一个“特征成分”，占据不同的频带，带宽由信号本身的特点所决定。EMD完全在时域进行，因而是一种很好的信号预处理方法。

图3 客车轴承振动信号经验模式分解

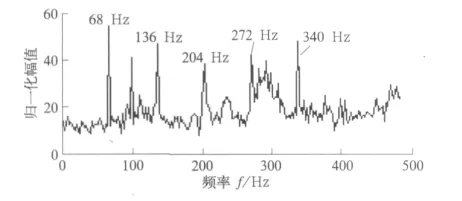
图4 轴承振动信号IMF c分量的1维谱45

注意到IMF c4和c5分量占居大约10～500 Hz频带，将二者合并，形成一个新分量c45，图4为c45分量的1维谱（平均64次）。图中可见在68 Hz，136 Hz，204 Hz，272 Hz和340 Hz出现清晰的谱线，为间隔68 Hz的频带，表明轴承振动信号中存在二次相位耦合。68 Hz是轴承外圈故障特征频率，由此判断轴承外圈出现损伤。试验过程中，轴报系统显示轴承温度正常。跟踪车辆轴承，在车辆回库检修时将其拆解，发现轴承外圈存在划伤，证实了诊断结论。用经验模式分解和1维谱相结合分析轴承振动信号能有效提取轴承故障二次相位耦合特征，比使用温度信号更早发现轴承故障。

4 结束语

25型客车振动信号包含丰富的车辆工作状态信息。经验模式分解相当于自适应滤波器组，能将信号分解成不同频带的固有模态函数。用于车辆振动信号分析可以抑制噪声和其他频带信号的干扰，将故障特征信息突出出来。1维谱能有效抑制高斯噪声，检测信号的二次相位耦合。经验模式分解与1维谱相结合，能有效提取车辆轴承故障特征，实现铁路客车轴承的早期故障诊断。

［1］孙惠琴，钟 原．小波分析与Hilbert变换在25T型客车故障诊断中的应用［J］．铁道机车车辆，2010，30（2）：38－42．

［2］黄采伦，樊晓平，陈春阳，等．基于小波系数提取及离散余弦包络分析的机车牵引齿轮故障诊断方法［J］．铁道学报，2008，30（2）：98－102．

［3］唐德尧．广义共振、共振解调故障诊断与安全工程－铁道篇［M］．北京：中国铁道出版社，2006．

［4］樊养余，陶宝祺，熊 克．舰船噪声的1维谱特征提取［J］．声学学报，2002，27（1）：71－76．

［5］高 飞，卢必昌，杨江天．机车牵引负荷试验轴承检测诊断系统［J］．铁道机车车辆，2007，27（5）：35－37．

［6］HUANG N E，SHEN Z，LONG S R．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］．Froc．R．Soc．Lond．A，1998，454：903－995．

［7］FLANDRIN P，RILLING G，GONCALVES P．Empirical mode decomposition as a filter bank［J］．IEEE Signal Processing Letters，2004，11（2）：112－114．