Visual Modflow在地下水污染物运移模拟中的应用

1 研究区概况

所研究污染场区位于北京市区东南部,地貌上属于永定河冲洪积扇的中下部,场区地形基本平坦,地面以下30m深度范围内一般存在2个含水层,局部区域有上层滞水,单层含水层厚度一般小于10m,仅部分地区大于10m。本文只研究埋深在10～20m的含水层和埋深在25m左右的承压含水层以及它们之间的黏土弱透水层,鉴于此,模型在空间上概化为3层:潜水含水层、弱透水层和承压含水层。

场区目前潜水流向由北向南,北部边界是侧向补给边界,主要接受侧向补给,南部边界为整个含水层系统的微量流出边界,由于地下水整体流向由北向南,故模拟区东、西两侧可以流线为边界,将它们设为隔水边界。承压含水层水流向由西北向东南,西北部为侧向补给边界,主要接受侧向补给,东南部为侧向流出边界,含水层底部大多为透水性较差的黏土地层,对系统内部影响很小,定义为隔水边界。

场区含水层分布广、厚度大,在常温常压下地下水运动符合达西定律,考虑浅、深层之间的流量交换以及软件的特点,地下水运动可概化成空间三维流;地下水系统的垂向运动主要是层间的越流,三维立体结构模型可以很好地解决越流问题;地下水系统的输入和输出随时间、空间变化,故地下水为非稳定流;参数随空间的变化体现了系统的非均质性,但没有明显的方向性,所以参数概化成各向同性。

2 地下水污染数值模拟

2.1 数学模型的建立

计算采用Visual Modflow软件进行模拟,在进行地下水模拟前,首先必须对模拟区进行矩形剖分。数值模型分潜水含水层、弱透水层和承压含水层共剖分50×50×3个单元。此外,研究重点是第四系松散孔隙潜水和第一承压含水层含水系统。系统的水均衡要素的补给项主要考虑大气降水入渗、边界侧向补给等,其他形式的补给作用相对较弱;排泄项主要考虑蒸发和边界侧向流出。

在不考虑水的密度变化条件下,孔隙介质中地下水在三维空间的流动可用偏微分方程来表示[2-3]:

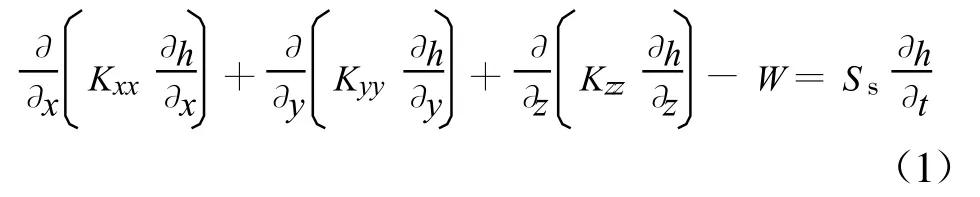
式中:Kxx、Kyy、Kzz分别为渗透系数在x、y、z方向上的分量;h为水头;W为在非均衡状态下通过均质、各向同性土壤介质单位体积通量,即地下水的源和汇;Ss为孔隙介质储水率;t为时间。

2.2 定解条件的处理

污染物在地下水中运移转化的过程是极其复杂的,不仅有对流、弥散作用,而且可能有离子交换、化学反应、微生物降解等化学和生物化学作用,在不同的环境下这些作用的方向和强度又有很大不同,本文只考虑对流和弥散作用。

地下水溶质运移满足下面的对流弥散方程:

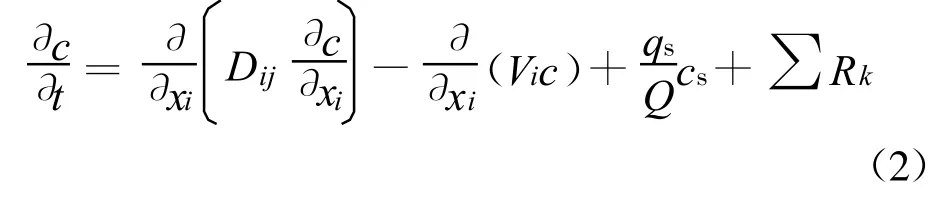
式中:c为地下水中污染物浓度;xi为沿坐标轴各方向的距离;Dij为水力扩散系数;Vi为地下水渗流速度;qs为源和汇的单位流量;cs为源和汇的浓度;Q为含水层孔隙率;∑Rk为化学反应项。

2.3 污染物质的确定

现场调查和地下水水质分析表明,研究区的污染情况相当复杂,并非仅有一个明显的污染源,而是可能存在一个主要的污染源和多个次要的污染源,可能的污染源主要来自管道渗漏和不符合标准的工业废水直接排放。参照美国EPA标准确定的严重污染物,研究区水质分析结果表明场区地下水的污染以单环芳烃和多环芳烃等特征污染物的污染最为突出,其中最为严重的是苯和萘2种污染物,利用Visual Modflow的MT3D模块对这2种污染物进行模拟。

2.4 模型的识别与验证

模型的识别与验证过程是整个模拟过程中的重要步骤,通常要进行反复修改参数和调整某些源汇项才能达到较为理想的拟合结果。模型的识别和验证主要遵循以下2个原则:①模拟的地下水流场要与实际地下水流场基本一致,即要求地下水模拟等值线与实测地下水位等值线形状相似;②识别的水文地质参数要符合实际水文地质条件。

根据以上原则,对模型进行识别,先给出各个参数的范围值,采用自动和手动相结合的方法,通过实际水位和计算水位的拟合分析判断,如果计算水位与实测水位相差大,则根据参数的变化范围和实际水位差值,再试给另一组参数,直至二者拟合较好为止,通过反复调整参数和均衡要素,识别水文地质条件,确定模型结构、参数和均衡要素。

2.5 参数的选取

因为本次模拟只考虑了对流和弥散的作用,所以溶质运移模型中系数的选取也只考虑弥散度、扩散系数和孔隙度。弥散度是建立地下水溶质运移模型中最难以确定的系数,一个重要原因是它的尺度效应,因此它的取值是当今弥散理论研究的一个热点,如李国敏等[4]综合世界范围内百余个水质模型中所使用的纵向弥散度与空间尺度的关系,认为水动力弥散的尺度效应具有分形特征,并给出了不同模型纵向弥散度尺度。综上所述,本次溶质运移模拟中拟采用的相关参数为:有效孔隙度0.1～0.35;有效扩散系数1.5×10-5m2/d;纵向弥散度10～30 m;垂向弥散度与纵向弥散度之比0.1;水平向弥散度与纵向弥散度之比0.1;降水入渗系数0.15;蒸发系数0.02。

3 模拟结果分析

根据目前该研究区污染物浓度,对苯和萘2种污染物分别进行预测,预测结果见图1、图2。

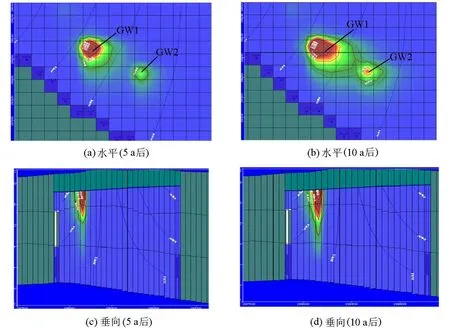
图1 苯的污染羽迁移模拟结果

图2 萘的污染羽迁移模拟结果

根据模型预测结果,由图1(a)、(b)可见,监测点GW1苯的污染羽比监测点GW2的污染羽大,运移到第10年的时候,前者沿水流方向总的污染距离约150m,后者沿水流方向总的污染距离约80m,这是因为监测点GW1的现状污染程度比GW2的现状污染程度大。从图1(c)、(d)可见,苯的污染羽在垂向上的迁移是从第一层慢慢向下面含水层渗透,在第6年的时候穿透中间的隔水层开始渗入到承压含水层。

从图2(a)、(b)可见,萘的污染羽随时间逐渐增大,但是相对于同一监测点GW1中萘的污染羽比苯的污染羽要小得多,运移到第10a的时候萘沿水流方向的污染距离约100m,小于苯的150m,这是因为萘的现状污染程度比苯的污染程度小。从图2(c)、(d)萘的污染羽在垂向上的迁移状况可见,萘的污染羽也是从第一层慢慢向下迁移,但是由于现状污染程度比较小,运移10年时没有穿透隔水层。

4 结论

a.污染物在地下水迁移过程中,由于机械弥散和对流的共同作用,污染范围的形状由最初近似圆形逐渐变为长轴方向与水流向一致的近似椭圆形。

b.污染物在含水层中随着地下水而迁移,在迁移过程中随着时间变化,苯和萘的污染羽中心都在随着地下水的流向迁移,污染范围逐渐增大。

c.溶质运移模拟显示,研究区最主要的污染源可能是位于GW1点周围的区域,另外可能还存在多处小的污染源。

d.污染场地的污染源不完全是点源,而本次模拟时按照点源(有限面源)的方式作了简化处理,降低了污染风险,建议尽早对该污染场地的地下水进行治理,以防污染物通过运移进入到承压含水层,造成更大的危害。

[1] 王克三.地下水污染及其监测治理问题[J].水文地质工程地质,1998(5):46-47.

[2] 郭卫星,卢国平.模块化三维有限差分地下水流动模型:美国地质调查局水资源调查技术丛书之六[M].南京:南京大学出版社,1999.

[3] MC DONALD M G,HARBAUGH A W.A modular threedimensional finite-difference ground-water flow model:U S Geological Survey Techniques of Water-Resources Investigations[M].Reston,Virginia:USGS,1988.

[4] 李国敏,陈崇希.空隙介质水动力弥散尺度效应的分形特征及弥散度初步估计[J].地球科学-中国地质大学学报,1995,20(4):405-409.