基础弹性刚度对铁路隔震曲线梁桥地震响应的影响研究

张 震

(中铁十二局集团第一工程有限公司，山西临汾 041000)

随着现代交通系统的日益发展，对线形、美观和功能的要求越来越高，曲线桥梁的需求量也越来越大。自1971年SanFernando地震中发生了曲线梁桥破坏之后，国内外研究者开始关注曲线桥梁的抗震问题:Tseng和Penzien开发了计算曲线和直线桥梁的程序，David Williams和Kawahiwa分别对SanFernando地震中破坏的一座曲线桥梁进行了振动台模型试验和计算分析，Godden首次进行位于十字路口上高架桥曲线桥梁的抗震试验，李国豪则用有限元法分析了曲线桥梁的地震反应，提出了一种每节点8自由度的曲线梁单元，并将计算结果与直线梁单元模拟的计算结果进行了比较。在这之后，则有更多的学者对曲线桥梁的动力特性计算、时程分析、构造方面的问题进行了大量的研究。但是，对曲线桥梁的动力特性分析，主要针对公路曲线桥梁进行了大量的研究工作，对铁路曲线梁桥的动力分析进行得较少[1]。

土-结构相互作用对系统的动力学参数有重要影响，进而影响结构的地震响应，因此，土的刚度及阻尼参数对桥梁结构地震响应的影响越来越受到人们的关注[2]。在阪神地震后，日本在改订桥梁抗震规范时，已经把上部结构-基础-地基的相互作用作为一个重要因素来考虑[3]。

减隔震措施在我国铁路桥梁工程中已有应用，国内很多学者也对铁路桥梁的减隔震措施进行了很多相关研究[4～9]，本文计算的曲线铁路梁桥便使用了研究相对较多的铅芯橡胶支座。本文基于M法，在不同的基础弹性刚度下，对具有硬土质基础的铁路隔震曲线梁桥在不同地震激励作用下进行了地震响应分析，研究了其地震响应的变化规律，取得了一些有价值的结果，为依据M法对具有硬土质基础的铁路曲线梁桥进行抗震设计提供了重要参考。

1 结构分析模型及地震激励的选取

1.1 结构分析模型

以某隔震铁路连续曲线梁桥为例，研究基础弹性刚度对隔震曲线梁桥地震响应的影响。该桥为一3跨连续曲线梁桥，曲率半径为500 m，跨径组合为35 m+60 m+35 m，桥墩均为实心矩形截面，采用C30混凝土浇筑，其中墩高度为9 m，边墩高度为10.5 m。桥墩编号为1～4号，结果分析时以典型桥墩3号中墩为例。3号墩的基础为3×2的群桩基础，桩直径为1.2 m，桩长25 m，采用C30混凝土灌注。

计算时建立全桥模型，各墩底部约束方式如图1所示，以模拟基础弹性刚度。计算基于大型通用软件ANSYS，主梁采用 BEAM44单元模拟，桥墩采用BEAM4单元模拟，铅芯橡胶支座采用COMBINE39单元模拟，基础对结构的影响通过矩阵单元MATRIX27单元实现。

1.2 铅芯橡胶支座力学模型

铅芯橡胶支座(LRB)采用简化的双向恢复力-位移滞回理论模型，如图2所示。

图1 墩底约束形式

图2 铅芯橡胶支座滞回模型

其中，Fy、dy分别为支座的屈服力和屈服位移;Fu、du分别为支座的水平极限承载力和极限位移;ku、kd则分别为支座的屈服前刚度和屈服后刚度;支座硬化比 η=ku/kd。

1.3 地震激励的选取

该桥处于一类场地，场地基本设防烈度为8度，因此在分析中，选用了7条一类场地条件下的实际地震地面加速度记录作为激励输入。地震激励的输入方向则分别为两桥台连线方向、与两桥台连线垂直的水平方向和竖向。各地震波记录特性如表1所示。

表1 各地震波记录特性

2 基础弹性刚度对地震响应的影响研究

2.1 利用“M法”确定基础弹性刚度

目前，我国铁路桥梁以及公路桥梁的设计规范中，当桩基础承受水平荷载、竖向荷载或弯矩的作用时，基础的刚度由“M法”计算得到。计算弹性支承刚度的具体步骤为[10]:首先，根据桩基础的具体情况，计算确定各桩单桩桩顶刚度;其次，根据各桩的排列，利用式(1)～(4)确定基础的各个弹性刚度系数。

(1)基础横向弹性刚度系数

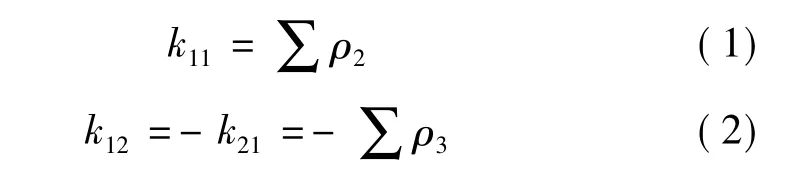
(2)基础竖向弹性刚度系数

(3)基础转动弹性刚度系数

其中，ρ1、ρ2、ρ3和 ρ4为各单桩桩顶刚度。

本文分析的铁路曲线梁桥，依据“M法”计算得到m=30 000 kPa/m2时的基础刚度系数如表2所示。

表2 m=30 000 kPa/m2时的基础刚度系数

2.2 不同基础弹性刚度下曲线梁桥的地震响应

本例中的曲线梁桥所处场地为一类场地，根据3号桥墩所处位置的土层特性，按照规范规定，m取值范围 为30 000～80 000 kPa/m2，以m=30 000 kPa/m2时计算得到的基础弹性刚度值为基准，定义其他m值所对应的基础弹性刚度与m=30 000 kPa/m2时对应的基础弹性刚度值的比值为基础刚度变化系数。故该桥所处场地的基础刚度变化系数变化范围为1.0～2.667。同时，为了更好的研究基础刚度对曲线梁桥地震响应的影响规律，本文还对基础刚度变化系数在0.2～1.0变化时的情况进行了地震响应的计算。

本次研究通过改变基础刚度变化系数，对不同情况分别进行地震响应时程分析计算，得到7个不同的实际记录地震激励下的该桥主梁最大扭矩、墩顶最大位移和墩底最大剪力、弯矩。

通过计算发现，本例中基础刚度的变化对典型桥墩墩顶顺桥向位移、墩底切向剪力和墩底径向弯矩的影响较其对墩顶横桥向位移、墩底径向剪力和墩底切向弯矩的影响为大，且规律相似，又限于篇幅，故只列出典型桥墩主梁最大扭矩、墩顶最大顺桥向位移、墩底最大切向剪力和墩底最大径向弯矩等计算结果，如图3～图6所示。

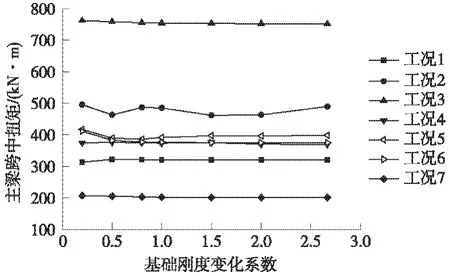
图3 主梁跨中扭矩变化

由图3可以看出，基础刚度变化对主梁最大扭矩的影响不是非常明显，基本保持同一水平。通过计算得知，各工况变化率都低于10%，其中除工况2、工况5和工况6的变化率较大，分别为6.87%、7.39%和8.74%之外，其他工况变化率均在5%以下。此外，在本例的地震激励输入方向下，主梁最大扭矩全部出现在曲线梁桥的边跨处，由两边跨向桥中跨主梁跨中扭矩逐渐减小。

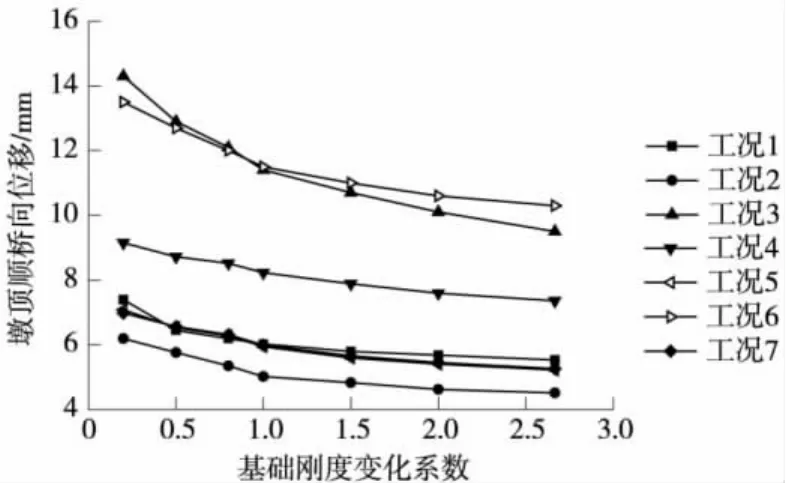
图4 墩顶顺桥向位移变化

由图4可以看出，随着基础刚度的增大，墩顶顺桥向最大位移呈减小趋势，变化明显，且随着基础刚度的增加减小趋势明显变缓。通过计算得知，各工况变化率均大于10%，其中工况 3变化率最大，达到了33.57%，而变化率最小的工况4也达到了19.52%。

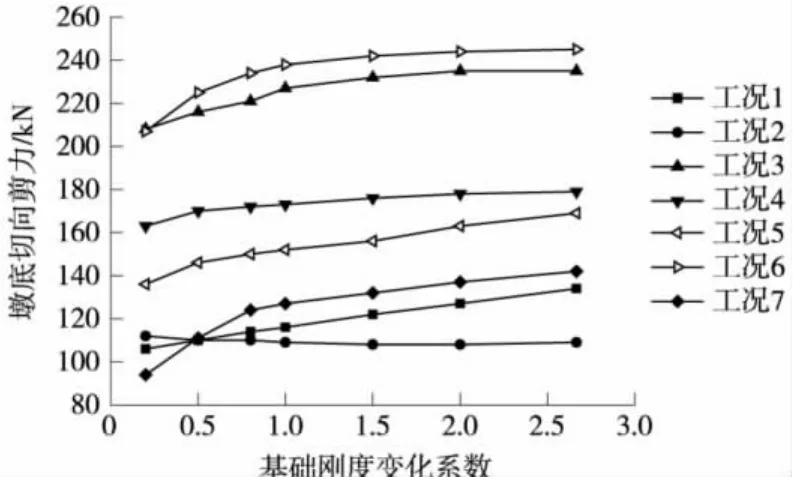
图5 墩底切向剪力变化

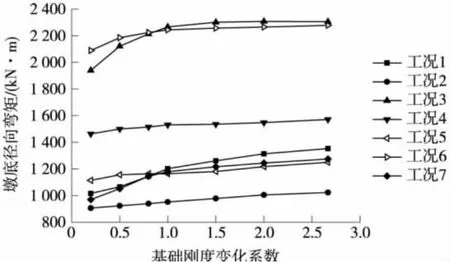
图6 墩底径向弯矩变化

由图5、图6可以看出，随着基础刚度的增大，除了工况2墩底最大切向剪力略有减少之外，其他工况下，墩底最大切向剪力和墩底最大径向弯矩大致呈增长趋势，且增长趋势随基础刚度的增加变缓。通过计算得知，工况2墩底最大切向剪力变化率最小，减少了4.18%;另外6种工况中，墩底最大切向剪力除工况4增长率较小，为8.93%之外，其他工况增长率均在10%以上，其中工况7增长率最大，达到33.75%;墩底最大径向弯矩除工况4和工况6变化率较小，分别为6.87%和8.30%之外，其他工况变化率均大于10%，其中工况1变化率最大，达到了24.9%。

因此，在进行曲线梁桥抗震设计时，对不同m值情况下桥梁的抗震性能进行验算是很必要的。

3 结论

(1)本例中，曲线梁桥受到地震激励作用时，随着基础刚度的变化，主梁跨中最大扭矩的变化并不很大，变化率均在10%以下，且大部分低于5%。同时在本例的地震激励输入方向下，主梁最大扭矩出现在曲线梁桥的边跨处，由两边跨向桥中跨主梁跨中扭矩逐渐减小。

(2)基础刚度的变化对墩顶横桥向位移、墩底径向剪力和墩底切向弯矩的影响小于对墩顶顺桥向位移、墩底切向剪力和墩底径向弯矩的影响，且对这两方面的影响规律相似。

(3)地震激励作用下，随着基础刚度的增大，墩顶顺桥向位移呈较明显的减小趋势。各工况变化率均大于10%，最小为19.52%，最大达到33.57%。虽然本例中顺桥向位移绝对值并不大，但基于其变化率很大，在抗震设计中应给予足够重视。

(4)随着基础刚度增大，除工况2墩底最大切向剪力略有减小外，其他墩底最大切向剪力和墩底最大径向弯矩都呈增大趋势，且趋势逐渐变缓。其中最大切向剪力和最大径向弯矩的最大变化率分别达到了33.75%和24.9%。由此可见，在曲线梁桥的抗震设计中应充分考虑基础刚度的影响，对m的取值进行适当的验算，以确保桥梁在地震作用中的安全性和可靠性。

[1]单德山，李 乔.铁路曲线梁桥抗震设计分析[J].重庆交通学院学报，2005，24(1):1.

[2]A.G.Vlassis，C.C.Spyrakos.Seismically isolated bridge piers on shallow soil stratum with soil－structure interaction[J].Computers and Structures，2001，79:2847-2861.

[3]孙立民，范立础.阪神地震后日本抗震规范的改订[J].同济大学学报，2001，29(1):60-64.

[4]杨风利，钟铁毅，夏禾.铁路简支梁桥减隔震支座设计参数的优化研究[J].铁道学报，2006，28(3):128-132.

[5]朱东生，劳远昌，等.隔震桥梁设计参数研究[J].土木工程学报，2000，33(5):53-56.

[6]郭磊，李建中，范立础.大跨度连续梁桥减隔震设计研究[J].土木工程学报，2006，39(3):81-85.

[7]王丽，阎贵平，方有亮.隔震桥梁非线性地震反应分析[J].北方交通大学学报，2002，26(1):80-84.

[8]钟铁毅，杨风利，吴彬.铅芯橡胶支座隔震铁路简支梁桥双向地震响应分析[J].中国铁道科学，2007，28(3):38-43.

[9]彭伟，李建中.减隔震连续梁桥非经典阻尼问题与地震响应简化分析[J].振动与冲击，2009，28(1):146-151.

[10]TB 10002.5—2005，铁路桥涵地基和基础设计规范[S].