并行组合扩频超宽带系统的跳时多址接入性能*

姜晓斐 郭黎利 齐琳 赵冰

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001)

2002年，美国联邦通信委员会(FCC)发布了超宽带(UWB)无线通信的初步规范，将超宽带信号定义为:任意相对带宽大于20%或者绝对带宽大于500MHz并满足功率谱密度限制要求的信号.这是超宽带技术真正走向商业化的一个里程碑，也促使其成为无线通信领域的研究热点之一［1］.目前超宽带通信的实现方式可分为两种:脉冲无线电(IR)和载波调制方式(MB-OFDM).本研究是基于脉冲无线电方式进行的.

超宽带的多址接入主要有跳时多址接入(THMA)、直接序列多址接入(DSMA)和脉冲波形多址接入方式(PSMA)等.文献［2］中提出一种基于多域协同的脉冲超宽带系统多址的通信方法，以解决随着用户数增多，超宽带系统中不同用户信号碰撞的概率增大，导致系统误码率较高的问题.文献［3-5］中将分数傅里叶变换引入超宽带系统，在分数傅里叶变换域进行滤波以实现降低多址干扰的目的.

并行组合扩频通信系统(PCSS)是在软扩频系统基础上发展而来的一种具有较高通信效率的扩频通信方式［6-7］.它既有扩频通信抗干扰、抗侦破的能力，又有很高的信息传输能力以及较高的频带利用率［8］.笔者将并行组合扩频系统融入超宽带系统中，构建一种新型的超宽带系统，即并行组合扩频超宽带(PCSS-UWB)系统［9］.它融合了并行组合扩频系统和超宽带系统各自的优点，进一步增加了超宽带系统的保密性能，而且较大程度地提高了系统的抗噪声性能.目前国内外关于这种新型超宽带系统的研究鲜见报道，文献［10］中分析了伪随机序列的选取对并行组合扩频超宽带通信系统的影响;文献［11-12］中分别建立了基于不同调制方式的并行组合扩频超宽带系统模型，指出并行组合扩频超宽带系统中并行组合扩频部分输出非等概的特点，并以此推导和验证了该系统基于多进制脉冲调制的解调差错概率;文献［13］中分析了并行组合扩频超宽带系统的信息传输能力以及发射参数与信息传输速率之间的关系;文献［14］中提出一种改进的并行组合扩频超宽带接收机结构，可提升系统的抗噪声性能.文中首次对该系统的多址接入能力进行分析，给出基于跳时多址接入方式的并行组合扩频超宽带多址通信系统模型，并对其进行了深入研究.

1 并行组合扩频超宽带系统

并行组合扩频超宽带系统是通过将并行组合扩频数据调制和解调后分别复合到超宽带的输入端和输出端来实现的.

1.1 并行组合扩频系统

并行组合扩频通信系统在发射端将输入的每k比特数据d1，d2，…，dk并串转换，然后送入数据——序列映射器，选出r个周期长度为N的正交扩频(PN)序列和某种序列极性，形成组合序列

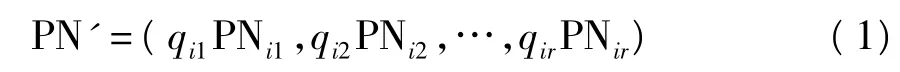
式中qia∈{ －1，+1}，a=1，2，…，r.这r个序列形成的组合序列进行对应码片的等幅度叠加(+1或－1值相加)，形成组合多值信号 MD(t)［8］:

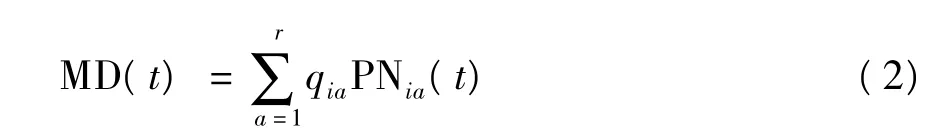
该多值信号共有r+1个数值输出.

经载波调制，并行组合扩频系统的发送信号为

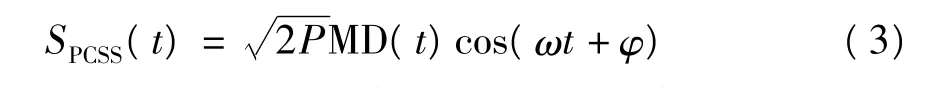
式中，P是一个序列的信号功率，ω为信号载波角频率，φ为信号载波初始相位，t为信号时间.

假设收发端载波同步，在接收端采用相干解调方式;在本地扩频码解扩之后，对其相关值的绝对值进行择大判决，选出最大的r路输出对应的扩频序列及其极性，依据数据——扩频序列逆映射算法，即可解调出原始发射信息.

并行组合扩频系统从M个正交扩频序列的集合中选择r个扩频序列以及序列的极性状态，然后经载波调制后发送，这样共有2r种发送状态，则能同时传送k=r+［log2］比特的信息数据［15］，其中表示从M个中取r个的组合数，［log2］表示对log2取整数部分.文献［6］中指出，并行组合扩频系统的最大信息数据传输比特数约为kmax=1.5N.

1.2 并行组合扩频超宽带系统模型

在发射端，将并行组合扩频系统的组合序列输出MD(t)作为超宽带系统的输入.由于MD(r，t)有r+1个状态，即为多值信号，因此对于并行组合扩频超宽带系统，后续处理需采用多进制的脉冲调制、解调方式，如多进制脉冲幅度调制(MPAM)、多进制脉冲位置调制(MPPM)、多进制双正交键控(MBOK)等，最终将调制后的数据送入脉冲形成器，以基带脉冲形式发射.采用MPPM的并行组合扩频超宽带系统框图如图1所示.

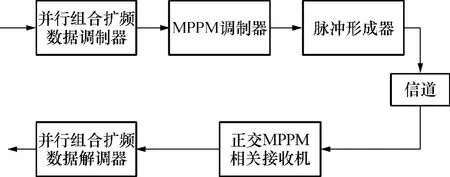
图1 采用MPPM的并行组合扩频超宽带系统框图Fig.1 Schematic diagram of PCSS-UWB system using MPPM

MD(r，t)经过重复编码后，进行MPPM调制，得到发射信号为

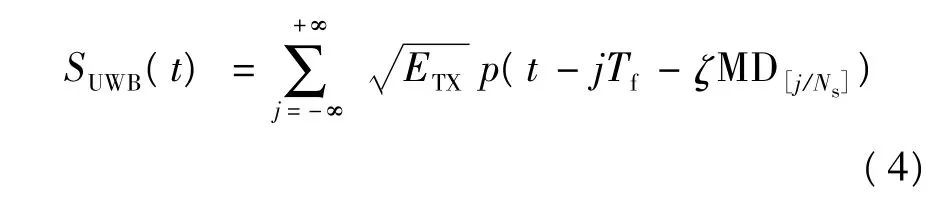
式中:Tf为无调制情况下的脉冲重复周期;p(t)是能量归一化的持续时间为wb的窄脉冲(wb远小于Tf);ζ表示由要传送的多进制符号MDj控制的发射脉冲时延;MDj∈{0，1，…，r}表示用户的MD序列的第j个码元;“［·］”表示取整运算，MD［j/Ns］表示每Ns个脉冲波形传送一个多进制符号.设为单脉冲的能量，则每比特的能量为

2 采用跳时多址接入方式的系统模型

假设系统是异步的，在上述系统模型中应用跳时多址接入方式，得到图2所示基于MPPM-THMA的并行组合扩频超宽带多址通信系统.第l个用户信息先经过并行组合扩频数据调制，得到MD(l)序列;再通过MPPM调制和用户所分配的跳时序列，控制发送脉冲的时间偏移量;第l个用户传输的信号为

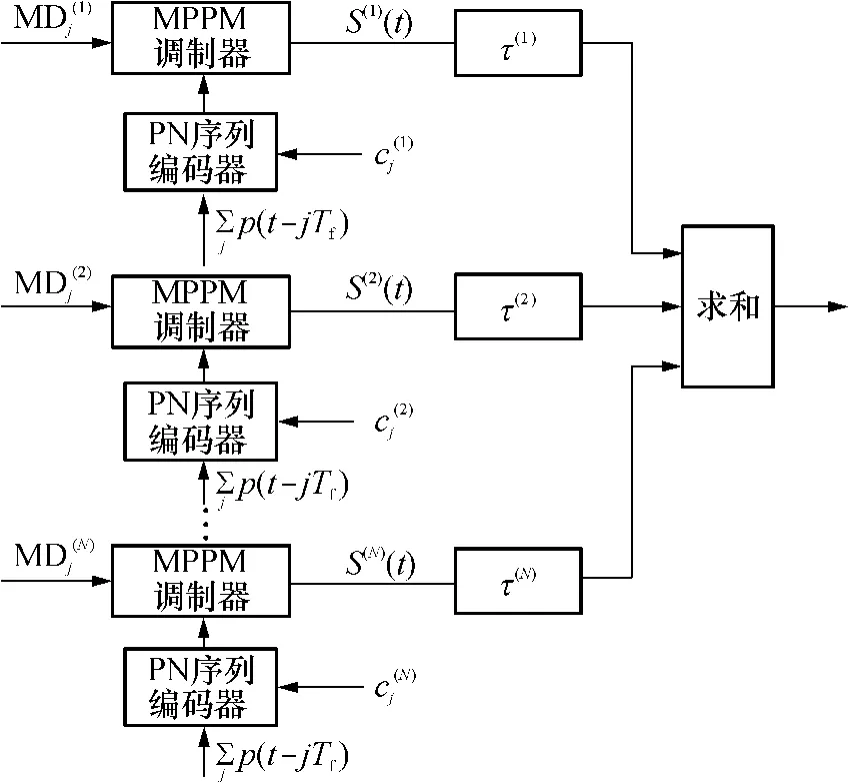
图2 基带发射端系统模型Fig.2 System model of base band transmitter

在接收端，采用单用户接收结构，如图3所示.假定信道为加性高斯白噪声信道，当γ个用户同时工作时，接收机解调用户1的信息.假设用户1的接收机与其发射机完全同步，即已知传输时延!1和信道衰落A1，接收信号RRX(t)表示为

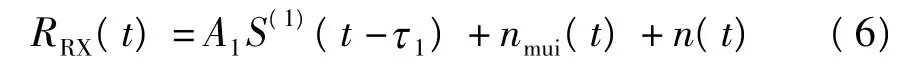
式中，nmui(t)和n(t)分别代表接收机输入端的多用户干扰和信道噪声.接收信号RRX(t)可以采用软判决检测或者硬判决检测方式进行检测，然后用正交MPPM相干接收方案进行MPPM解调，其中采用的模板信号为

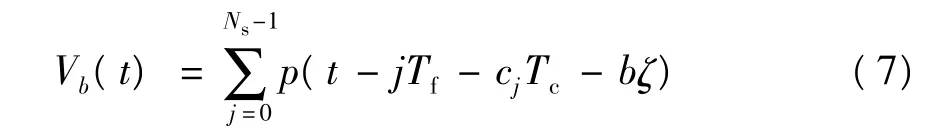
式中，b=0，1，…，r.解调后得到消除高斯噪声的并行组合序列进行并行组合扩频数据解调，即可恢复用户1的原始数据信息.

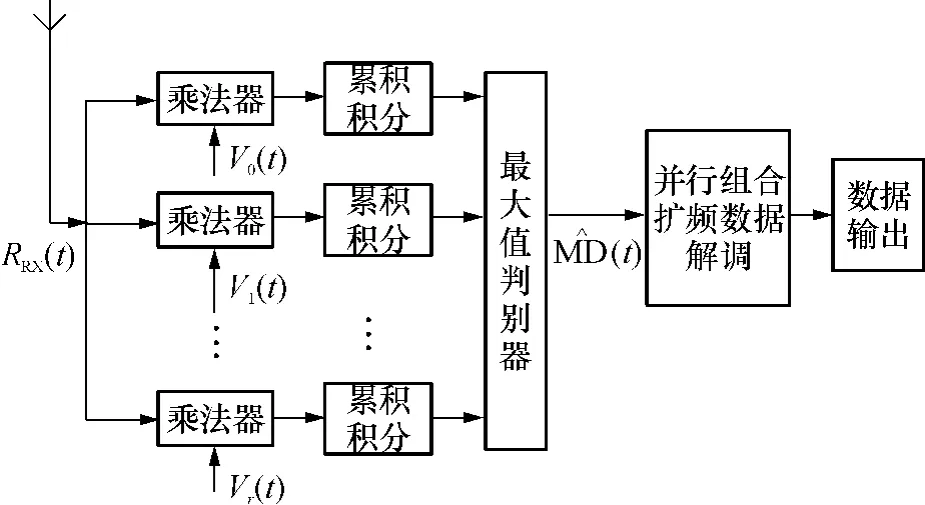
图3 单用户接收端系统框图Fig.3 Block diagram of single-user receiver system

3 仿真结果与分析

通过仿真，将提出的基于MPPM-THMA的并行组合扩频超宽带多址系统与传统的超宽带系统进行对比，分析跳时多址接入方式对所提出系统性能的影响.仿真所采用的超宽带脉冲为二阶高斯脉冲，重复编码数为3.并行组合扩频调制部分的正交扩频序列总数M=16，从中选取的序列数r=3，则可同时传输的数据k=12;正交扩频序列均采用周期N为63的平衡Gold码，数据序列映射采用改进r-组合映射编码算法［16］.系统采用4PPM调制方式.信源是独立同分布且等概率出现的，信道为加性高斯白噪声信道，假定单用户接收机已同步，得到图4所示系统误码率(BER)随信噪比(Eb/N0)变化的曲线.

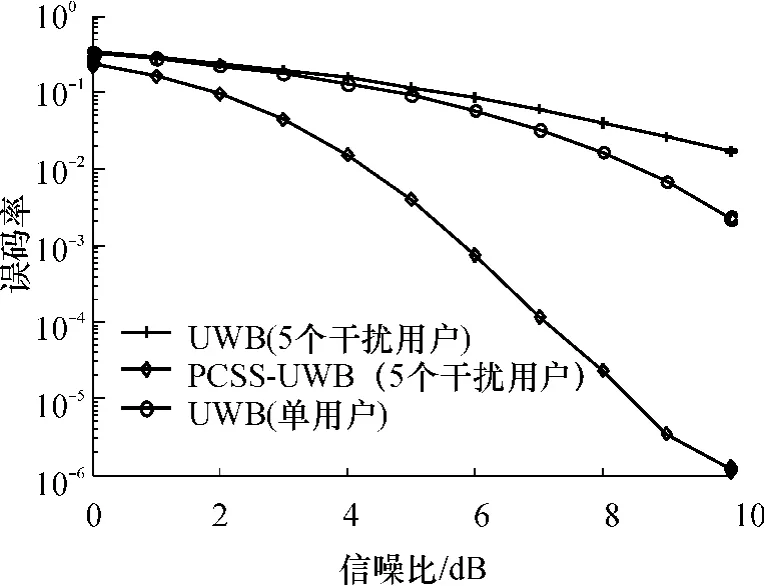
图4 多用户超宽带系统与并行组合扩频超宽带系统的误码性能对比Fig.4 Comparison of BER performance between UWB system and PCSS-UWB system

图4分别给出了6个用户的超宽带系统，即存在5个干扰用户条件下的超宽带系统以及并行组合扩频超宽带系统的平均误码率曲线和单用户超宽带系统理论曲线.图4中超宽带系统在进行6个用户的多址通信时，相对于单用户通信，误码性能发生恶化，不利于多址通信的应用，限制了超宽带系统用户容量的提升.文献［4-5］中提出的基于分数傅里叶变换域的多址方式以及文献［2-3］中所采用的基于分数傅里叶变换域的多址方式与时分多址结合的多域联合的多址技术，在6个用户的多址通信中，超宽带系统的误码性能都可以进一步地接近单用户超宽带系统的理论值，一定程度上提升了超宽带的系统容量.而文中所采用的方法在超宽带系统中融入了并行组合扩频技术，构建了一个崭新体制的超宽带通信系统，即并行组合扩频超宽带通信系统;并行组合扩频技术牺牲小部分的频带利用率，为超宽带系统提供了额外的扩频增益，可大幅优化系统的误码性能.在上述仿真条件下，该系统的数据传输速率与单用户超宽带系统相同，而由于并行组合扩频调制为其提供了N/k=5.25倍的扩频比，其平均误码率远优于单用户超宽带系统的误码率，从而使系统容量得到了大幅提升.进一步增加并行组合扩频超宽带系统的用户个数，仍采用MPPM-THMA多址方式，在图5中给出系统分别在5、20、50个干扰用户条件下的误码率曲线.当存在5个干扰用户时，误码率随着信噪比的升高而快速下降，即信道噪声是影响系统性能的主要因素，多用户干扰可忽略不计.而当存在20个和50个干扰用户时，系统的误码率趋向于一个常数;即在信噪比很高的条件下，系统的工作性能取决于多用户干扰因素.与传统的超宽带系统相比［17］，文中提出的方案在信噪比很高的情况下，当存在20个干扰用户时，其误码率约从10－3降至10－4;当存在50个干扰用户时，系统性能的提升已不明显，可以通过调整并行组合扩频调整参数M或者r来降低可同时传输的数据k，或者增加正交扩频序列的周期长度N来获得更高的扩频增益，从而提升系统的工作性能.

图5 不同干扰用户条件下并行组合扩频超宽带系统的误码性能Fig.5 BER performance of PCSS-UWB system under the conditions of different user numbers

将用户的信噪比固定为10dB，得到系统误码率随用户数γ变化的仿真曲线如图6所示.由图6可知，随着用户数γ的增加，多用户干扰不断增加，此时多用户干扰成为制约系统工作性能的主要因素，使得系统性能逐渐下降.可以考虑采用新的跳时码以减少脉冲间发生碰撞的概率，从而达到降低多用户干扰的目的.

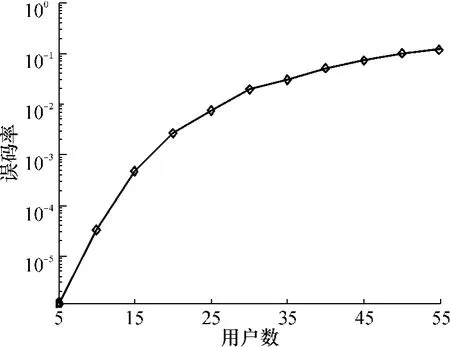
图6 用户数对并行组合扩频超宽带系统的影响Fig.6 Impact of user numbers on PCSS-UWB system

4 结语

针对并行组合扩频超宽带系统，文中提出采用MPPM-THMA的多址接入方式，并给出了其实现多址的系统模型.由于在传统的超宽带系统中融入了并行组合扩频技术，使得超宽带系统可获得额外的扩频增益，从而改善了系统的工作性能，提升了系统容量.仿真结果表明采用MPPM-THMA的并行组合扩频超宽带多址系统性能优于传统的超宽带系统，使得系统可容纳的用户数量有了较大的提高.下一步将分析并行组合扩频超宽带系统在采用其他多址接入方式下的系统性能，并与跳时多址接入方式进行对比，以得出最佳的多址接入方式或给出其各自的适用范围.

［1］张中兆，沙学军，张钦宇，等.超宽带通信系统［M］.北京:电子工业出版社，2010:1-6.

［2］宁晓燕，沙学军，邱昕，等.基于多域联合的脉冲超宽带多址技术［J］.哈尔滨工业大学学报，2008，40(增刊1):89-92.Ning Xiao-yan，Sha Xue-jun，Qiu Xin，et al.IR-UWB multiple access technology based on multiple domain cooperation ［J］.Jounal of Harbin Institute of Technology，2008，40(S1):89-92.

［3］邱昕，沙学军，宁晓燕.一种分数傅里叶变换域的超宽带多址方式［J］.华南理工大学学报:自然科学版，2010，38(9):20-24.Qiu Xin，Sha Xue-jun，Ning Xiao-yan.Multiple access scheme of Ultra-wideband system in fractional Fourier transform domain［J］.Journal of South China University of Technology:Natural Science Edition，2010，38(9):20-24.

［4］Sha Xue-jun，Wen Rong-hui，Qiu Xin.A new multiple-access method based on fractional Fourier transform［C］∥Canadian Conference on Electrical and Computer Engineering.St Johns:IEEE，2009:856-859.

［5］Lakshm inarayana H K，Bhat J S，Jagadale B N，et al.Improved chirp modulation spread spectrum receiver based on fractional Fourier transform for multiple-access［C］∥2009 International Conference on Signal Processing Systems.Singapore:International Association of Computer Science and Information Technology，2009:282-286.

［6］Zhu Jin-kang，Gen Marubayashi.Parallel combinatory SS communication ［J］.IEICE Technical Report of Japan，1990，SSTA90-23:34-42.

［7］Zhu Jin-kang，Shigenopu Sasaki，Gen Marubayashi.Proposal of parallel combinatory spread spectrum communica-tion system ［J］.IEICE Transactions on Communications，1991，74-BⅡ(5):207-214.

［8］衣强.并行组合扩频系统抗干扰技术及映射算法研究［D］.哈尔滨:哈尔滨工程大学信息与通信工程学院，2007:12-14.

［9］Qi Lin，Guo Li-li，Jiang Xiao-fei.Performance studies of UWB communication system based on parallel combinatory spread spectrum［C］∥The 5th International Conference on Wireless Communications，Networking and Mobile Computing.Beijing:Institute of Electrical and Electronics Engineering，Inc，2009:1-4.

［10］Jiang Xiao-fei，Guo Li-li，Wang Bai-ling，et al.Performance analysis for UWB system based on parallel combinatory spread spectrum using different pseudo noise sequences［C］∥2010 2nd International Conference on Education Technology and Computer.Chengdu:Institute of Electrical and Electronics Engineering，Inc，2010:213-216.

［11］齐琳，郭黎利.并行组合扩频非等概超宽带系统误码性能研究［J］.系统工程与电子技术，2011，33(3):659-664.Qi Lin，Guo Li-li.BER performance study of non-equal probability UWB system based on parallel combinatory spread spectrum ［J］.System Engineering and Electronics，2011，33(3):659-664.

［12］郭黎利，姜晓斐，窦峥.并行组合扩频超宽带通信系统建模与仿真［J］.哈尔滨工程大学学报，2011，32(4):499-503.Guo Li-li，Jiang Xiao-fei，Dou Zheng.Modeling of a UWB communication system based on a parallel combinatory spread spectrum and its simulation analysis［J］.Journal of Harbin Engineering University，2011，32(4):499-503.

［13］齐琳，郭黎利，姜晓斐.基于脉冲调制的并行组合扩频通信系统性能研究［J］.计算机应用研究，2011，28(6):2286-2288.Qi Lin，Guo Li-li，Jiang Xiao-fei.Performance studies of parallel combinatory spread spectrum based on pulse modulation ［J］.Application Research of Computers，2011，28(6):2286-2288.

［14］齐琳，郭黎利，姜晓斐.改进的并行组合扩频超宽带接收机性能［J］.北京邮电大学学报，2011，34(2):12-16.Qi Lin，Guo Li-li，Jiang Xiao-fei.A parallel combinatory spread spectrum based study on the improved UWB receiver［J］.Journal of Beijing University of Posts and Telecommunications，2011，34(2):12-16.

［15］李北明.并行组合扩频通信系统关键技术的研究［D］.哈尔滨:哈尔滨工程大学信息与通信工程学院，2004:4-6.

［16］王玫，郭黎利，于奇.基于改进r-组合映射编码并行组合扩频通信系统的分析［J］.船舶电子工程，2008，28(10):78-81.Wang Mei，Guo Li-li，Yu Qi.Analysis of coded parallel combinatory spread spectrum communication system based on improvedr-combinatory mapping ［J］.Ship Electronic Engineering，2008，28(10):78-81.

［17］贝尼迪特，吉安卡拉.超宽带无线电基础［M］.葛利嘉，朱林，袁晓芳，等，译.北京:电子工业出版社，2005:255-275.