微尺度重掺杂硅光栅波长选择性吸收率的数值研究

王爱华，蔡九菊

(东北大学 国家环境保护生态工业重点实验室，辽宁 沈阳，110819)

中红外波段选择性吸收对于热红外成像仪、人体温度监测的耳温计等许多实际应用具有重要意义。近年来，人们对一维光栅在中红外波段波长选择性发射或吸收进行了许多数值和实验研究。Hesketh等[1-2]最早开始了对微机械加工的重掺杂硅表面红外辐射特性的一系列研究。结果表明，在许多波长上横电波(Transverse electric wave，TE波)和横磁波(Transverse magnetic wave，TM 波)都表现出很高的发射率。TM波热辐射在10～12 μm波长区间内表现出相干峰，并且峰值强烈依赖于入射角度。另外，通过激发表面离子化激元可以获得硅光栅在可见光和近红外区域的发射角波瓣[3]。Marquier等[4-5]对由掺杂硅光栅构成的方向性和准各向同性2种热源的各相异性偏振热辐射进行了数值研究，分析了偏振方式和入射角度对于总的半球发射率的影响，同时对重掺杂硅表面的红外热辐射特性进行了数值模拟，发现通过改变掺杂浓度可以调节等离子体频率，同时通过利用表面等离子体激元可以大大改变远场的辐射特性。Laroche等[6]通过对掺杂硅发射率调整途径的研究发现：表面等离子体激元和行进波的有效耦合可以提高重掺杂硅器件的辐射通量。一般地，来自激元谐振的高发射率或吸收率在光谱中表现出很窄的峰值，并且峰值通常依赖于入射角度，除非它的频率与色散关系中的渐进支相匹配[7]。为了克服一维光栅应用中存在的吸收率光谱峰值窄、依赖于入射角度等不足之处，提出采用一维复杂光栅作为二维复杂结构的替代选择。所谓复杂光栅是指由2个或多个具有不同周期和几何特征的一维简易光栅叠加而成的光栅结构[8]。多个简易光栅之间的相互影响可以改变色散关系从而相应改变辐射特性[8-10]。同时，这些辐射特性可以通过在1个周期内带有多个凹槽的复杂光栅内进行强化或抑制[11]。虽然复杂光栅具有克服一维简易光栅缺点的潜力，然而，人们对于它具有的峰值波长调控的灵活性在中红外区域内的可应用性并没有进行深入研究。因此，为了设计TM波入射条件下的中红外波长选择性吸收器，需要探究重掺杂硅材料特性和表面几何对辐射特性的影响。选择重掺杂硅作为复杂光栅材料是因为它在微纳米制备中很普遍，并且它的光学常数可随掺杂浓度变化而变化。当载流子浓度很高时，硅具有导电性并且能够激发等离子体激元以调整其在中红外区的辐射特性。

1 理论基础

1.1 重掺杂硅的辐射特性

理解不同载流子浓度和掺杂物类型条件下重掺杂硅的辐射特性是本文研究的基础。垂直入射条件下平面重掺杂硅在真空中的光谱吸收率为[12-13]：

式中：αλ为光谱吸收率；nSi为Si的折射率；κSi为Si的消光系数。

图1所示为光谱波段2～15 μm之间p型和n型重掺杂硅的吸收率，其中，硼和磷的载流子浓度分别取1×1020，3×1020，5×1020和 1×1021cm-3。从图1(a)可知：对于载流子浓度NB=1×1020cm-3，吸收率最高值位于波长λ=6.1 μm处，为0.84；随后，吸收率逐渐降低，直至波长λ=15 μm处变为0.26。在短波长处，吸收率最小值在波长λ=0.5 μm处，约为0.68(在此未给出)[14]；当载流子浓度增加时(NB≥3×1020cm-3)，吸收率最大值对应的波长移向近红外区域并且峰值接近于0.9，随后，吸收率迅速降低至中红外区域；当载流子浓度为NB=1×1021cm-3时，吸收率在波长λ≥4 μm处低于0.2。当在光谱中出现高峰值时，低吸收率就会在选择性波长吸收中与其形成鲜明对比。对于n型重掺杂硅，图1(b)给出了类似的吸收光谱。换句话说，在确定重掺杂硅的光学常数时，载流子浓度比掺杂物类型更重要。

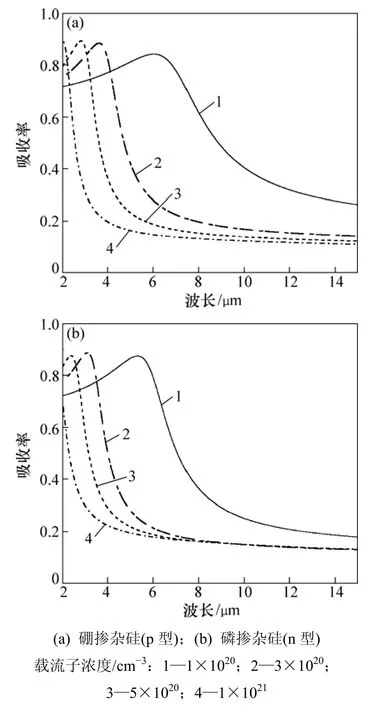
图1 平面重掺杂硅在垂直入射条件下的光谱吸收率Fig.1 Spectral absorptance of plain heavily doped silicon at normal incidence

1.2 几何形状

图2所示为重掺杂硅简易光栅和复杂光栅的几何形状。其中：Λ为光栅周期；f和g分别为栅脊高和栅谷宽。对于简易光栅，周期(Λ)只包括1个栅脊和1个栅谷，即Λ=h+f。一般地，入射平面由入射波和表面法线来定义。对于图2，入射平面设定在x–z平面，垂直于栅谷。在图2(a)中，只有横磁波能激发表面等离子体激元(Surface plasmon polariton，SPP)。光是从空气入射到光栅表面上，θ为入射角。光栅的几何是由脊高h、脊宽f和谷宽g来定义的。

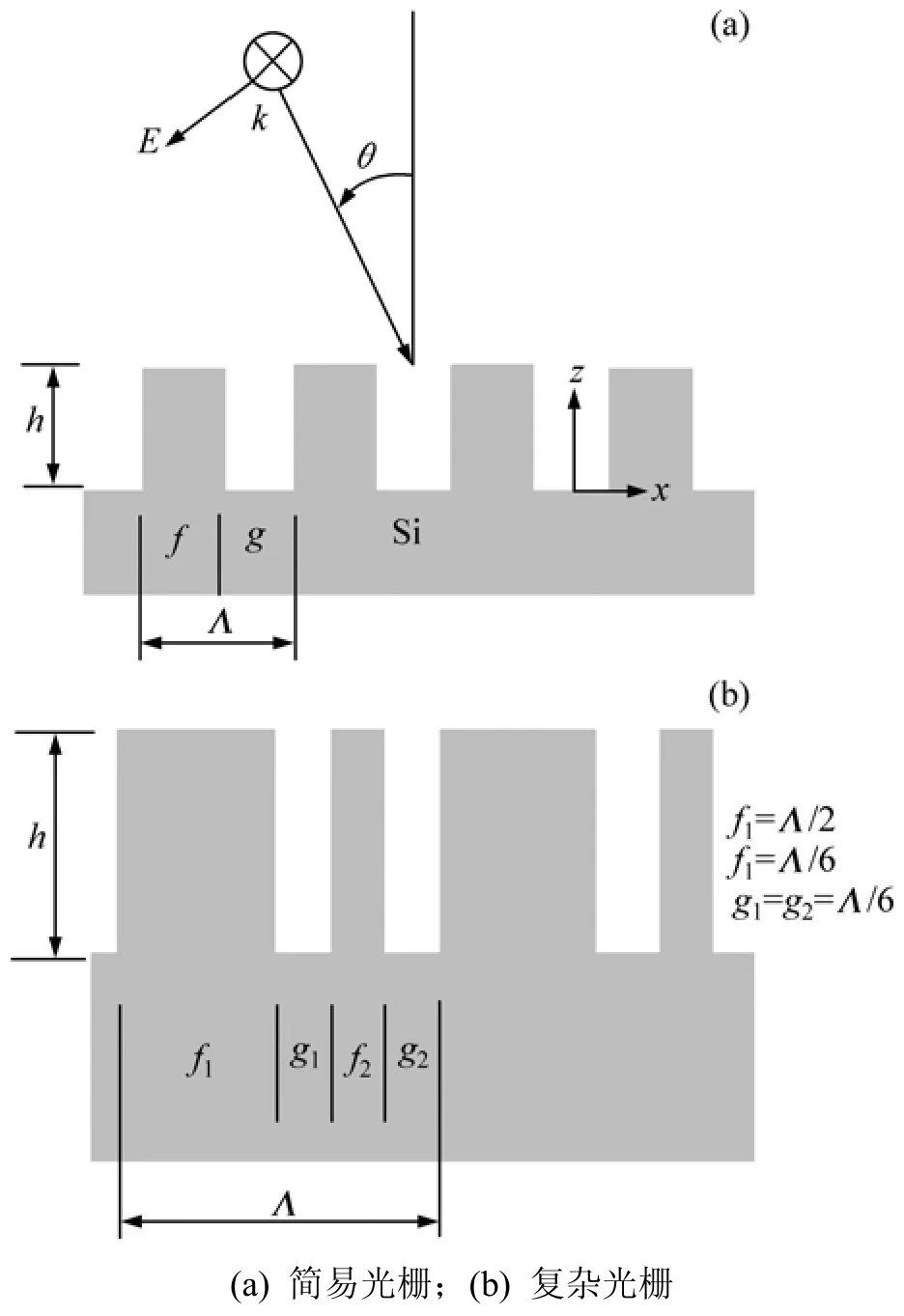
图2 简易光栅和复杂光栅结构示意图Fig.2 Schematic of simple and complex gratings

图2(b)所示为一基本的复杂光栅。需要说明的是，复杂光栅的特征可以非常复杂，例如正弦函数的叠加[9]或者是由不同的材料组成[15]。这里复杂光栅的轮廓生成是通过1个短周期简易光栅和1个长周期简易光栅合成的。在1个周期内包含了1个宽脊(f1=Λ/2)、1个窄脊(f2=Λ/6)和2个宽度相同的栅谷(g1=g2=Λ/6)，其特征是由1个周期为Λ=4/3 μm的短周期光栅和1个周期为Λ=8 μm的长周期光栅合成的。对于任一复杂光栅，尺寸由其周期和高度来决定，如图2(b)所示。假设掺杂硅足够厚并且可当作沿z轴的正轴方向的半无限来模拟，则其透射率(τ)就可以假定为 0。一旦计算获得反射率(ρ)，吸收率(α)就可以基于能量平衡原理计算得到：α=1-ρ。

1.3 时域有限差分法

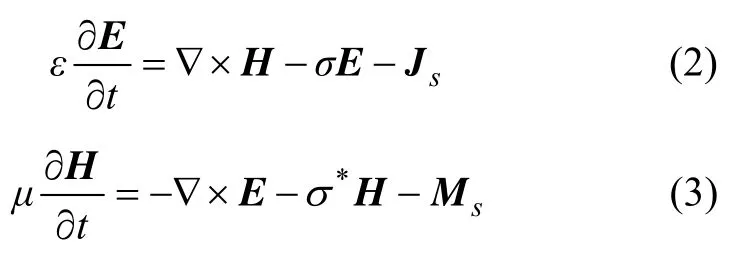
时域有限差分法(Finite difference time domain,FDTD)可以对电磁波的麦克斯韦方程进行直接数值求解。对于线性、各向同性材料，电磁波的麦克斯韦方程形式为[16]：式中：E为电场强度，V/m；H为磁场强度，A/m；Js为电场的电流密度，A/m2；Ms为磁场的磁通密度，Wb/m2；ε为介电常数，F/m；μ为磁导率，S/m；σ为电导率，S/m；σ*为等效磁阻率，Ω/m。在这里，Js和Ms均为0。麦克斯韦方程可以分解为相互独立的2组方程，其中一组是TE波，另一组是TM波。将电场和磁场的各向量分量代入方程组，可以得到二维 TE波方程组为：

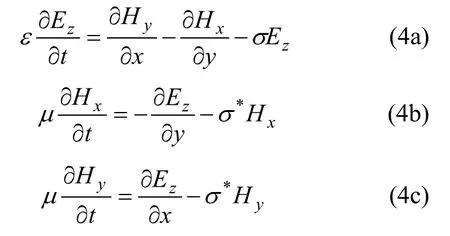
同样，可以获得TM波方程组的各分量：Hz，Ex和Ey。实际上，TM波方程组是TE波方程组的对偶形式。

具体的数值算法、周期性边界处理、理想匹配层吸收性边界条件以及二维几何条件下TE波和TM波二阶中心差分解的形式见文献[16]。

2 简易光栅的光谱吸收率

2.1 不同填充比条件下简易光栅的光谱吸收率

图3所示为TM波p型硅简易光栅在不同填充比条件下的光谱吸收率，其中，NB=1×1021cm-3，h=0.6 μm，光栅的周期分别为Λ=6.3 μm和Λ=7.3 μm，入射角度均为0°。由图3可见：不同填充比条件下的光谱吸收率曲线均存在峰值，其中填充比f/Λ=0.4的吸收率峰值接近于1，这是由于表面等离子体激元(SPP)的激发；而填充比f/Λ=0.1的峰值要远远低于填充比f/Λ=0.4时的峰值，仅有0.3左右，这是因为表面波的耦合受到了辐射和表面特征之间相互作用的影响；另外，随着光栅周期的增大，吸收率峰值位置向长波段移动。此处的峰值与相对较低载流子浓度NB=5×1020cm-3条件下的结果非常相似[4]。

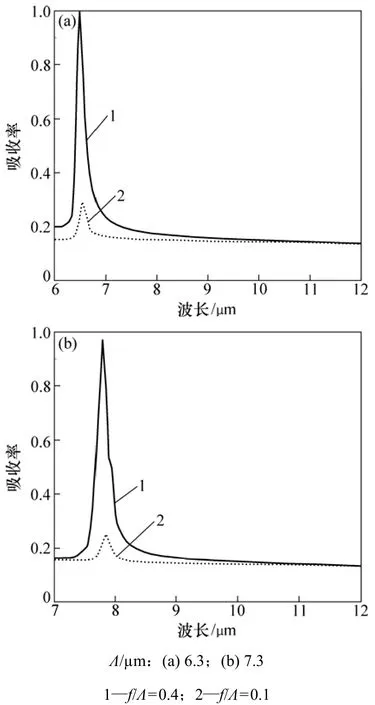
图3 TM波p型重掺杂硅简易光栅的光谱吸收率Fig.3 Spectral absorptance of p-type simple gratings made of heavily doped silicon for TM waves

2.2 不同载流子浓度条件下简易光栅的光谱吸收率

图4所示为TM波n型硅简易光栅在不同载流子浓度条件下的光谱吸收率，其中载流子浓度NP分别为1×1021和3×1020cm-3。这里，2种算例的填充比、脊的高度和入射角均相同，分别为f/Λ=0.4，h=0.6 μm和θ=0°；光栅周期Λ分别为6.3 μm和7.3 μm。当载流子浓度增加时，很显然吸收率峰值位置移向短波段，并且峰值的半峰全宽(Full-width at half- maximum，FWHM)有所减小。然而，不管载流子浓度如何变化，峰值几乎相同。与普通重掺杂硅表面的吸收率相类似，图3和图4表明：具有相同载流子浓度(N=1×1021cm-3)、不同注入材料(硼和磷)的简易光栅的吸收率在波长为6～12 μm的区域非常相似。

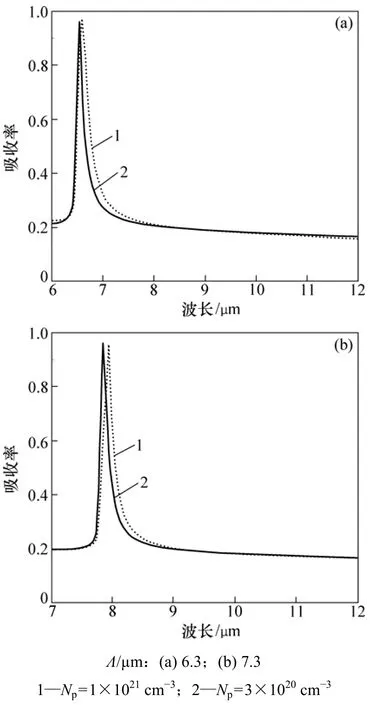
图4 TM波n型重掺杂硅简易光栅的光谱吸收率Fig.4 Spectral absorptance of n-type simple gratings made of heavily doped silicon for TM waves

3 复杂光栅的光谱吸收率

3.1 与简易光栅的对比

为了证明复杂光栅作为波长选择性吸收表面的优势，对简易光栅和复杂光栅垂直入射条件下的光谱吸收率进行对比，结果如图5所示。2种光栅的组成材料均为p型硅，载流子浓度为NB=1×1021cm-3，脊高和光栅周期也相同，分别为Λ=6 μm和h=4 μm。简易光栅的横向脊宽与复杂光栅 I的脊宽之和相同，即f=f1+f2=2Λ/3。

由图5可知：复杂光栅I的光谱吸收带明显比简易光栅的宽。虽然复杂光栅吸收率峰值比简易光栅有所降低，但是其FWHM为1.35 μm，明显超过简易光栅的 0.78 μm。对于简易光栅，不管载流子浓度、特征尺寸和其他参数如何变化，也无法获得与复杂光栅相当的光谱吸收率。

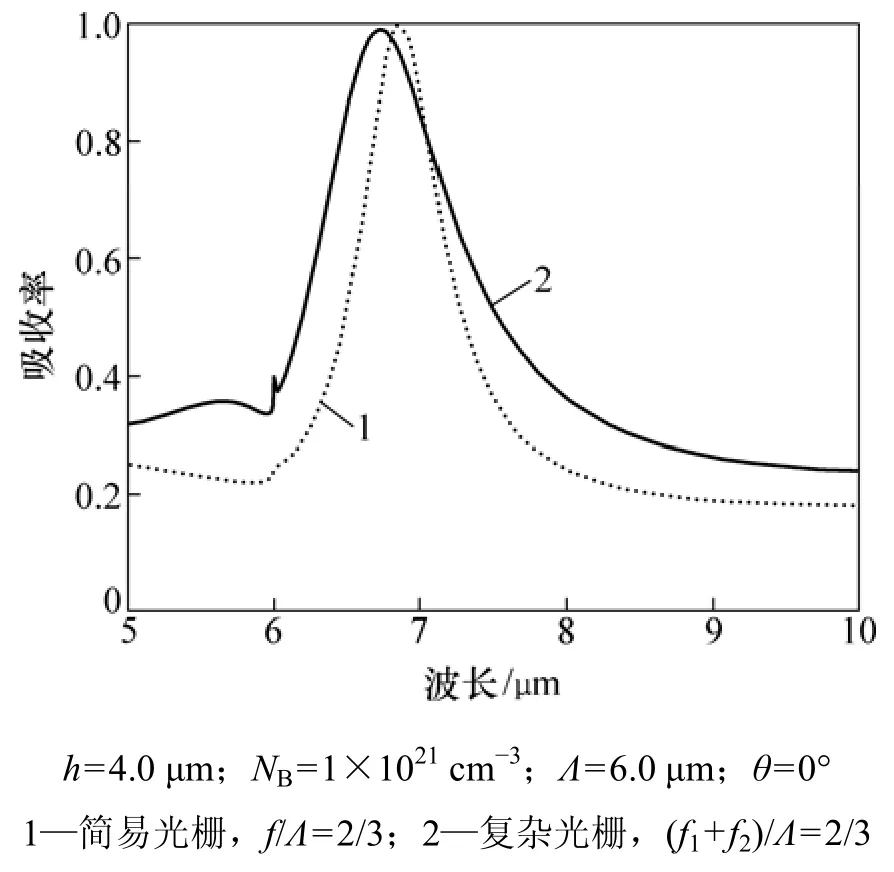
图5 垂直入射条件下简易光栅和复杂光栅光谱吸收率的对比Fig.5 Spectral absorptance of simple grating and complex grating at normal incidence

3.2 磁场与坡印廷向量分布

图6所示为复杂光栅的时间平均坡印廷向量和磁场y轴对数标幅值平方(lg10|Hy|2)分布。图中入射光沿z轴方向行进，因为入射平面是在x-z平面，所以，Hy中的下标y是指y分量。坡印廷向量经过了与入射向量的归一化处理，入射波长为吸收率峰值所对应的波长 10.15 μm。

图6(a)所示为复杂光栅I在垂直入射角度下光栅区域周围的时间平均坡印廷向量分布。图中箭头长度代表了坡印廷向量的大小，箭头指向为坡印廷向量方向和净能量流向路径。可以看出：通过两栅脊之间区域的坡印廷向量值要比光栅上方的向量值大，因此，用较长的箭头表示。需要指出的是：进入栅脊内部的坡印廷向量迅速衰减(这里没有给出)，能量从光栅表面挤入到狭窄的栅谷内，反射率可以忽略。除了在硅栅拐角处之外，栅脊之间区域的坡印廷向量相同并且均匀分布。图6(b)所示为复杂光栅1个周期内完整的磁场。很显然，光栅上方的磁场幅值平方要比光栅内部和光栅底部的大得多，并且它沿坡印廷向量的行进方向不断降低。同时，在栅脊内部的磁场幅值平方逐渐降低直至达到最小值。

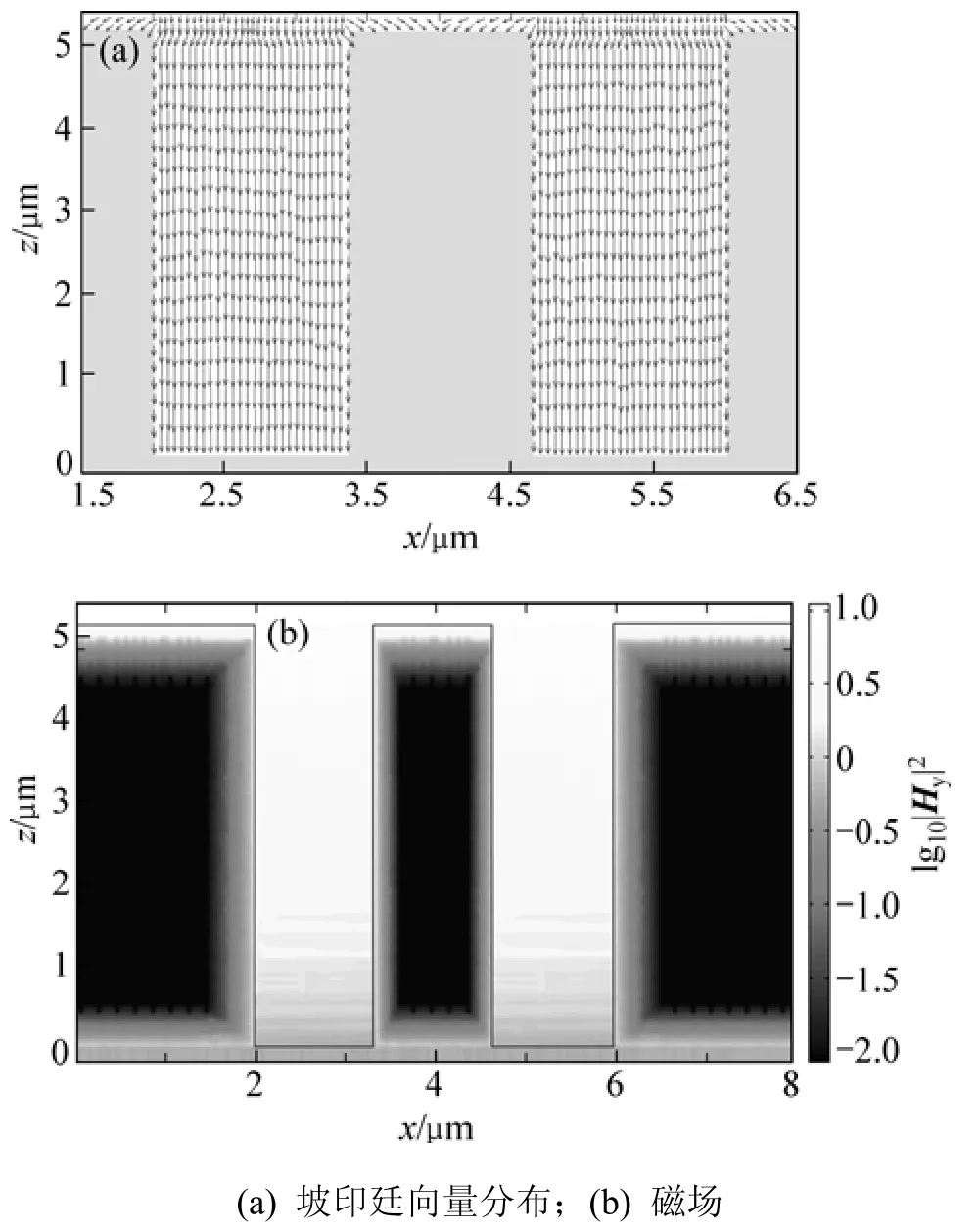
图6 复杂光栅的坡印廷向量和磁场y轴对数标幅值平方(lg10|Hy|2)分布(入射角度为0°，入射波长为10.15 μm，对应的吸收率为0.942)Fig.6 Poynting vector and magnitude square of complex magnetic field in logarithmic scale for complex grating at θ=0°,λ=10.15 μm and absorptance of 0.942 in this case

4 结论

(1) 对于微尺度重掺杂硅简易光栅，不同填充比条件下的光谱吸收率曲线均存在峰值；随着光栅周期的增大，吸收率峰值位置向长波段移动。

(2) 当载流子浓度增加时，简易光栅吸收率峰值位置移向短波段并且半峰全宽值有所减小。然而，不管载流子浓度如何，峰值几乎相同。具有相同载流子浓度、不同注入材料(硼和磷)的简易光栅的吸收率曲线在波长为6～12 μm区域间非常相似。

(3) 复杂光栅的光谱吸收带明显比简易光栅的宽，这说明复杂光栅具有比简易光栅更优良的性能。

[1]Hesketh P J,Zemel J N,Gebhart B,et al. Organ pipe radiant modes of periodic micromachined silicon surfaces[J]. Nature,1986,324: 549-551.

[2]Greffet J J,Carminati R,Joulain K,et al. Coherent emission of light by thermal sources[J]. Nature,2002,416: 61-64.

[3]Kreiter M,Oster J,Sambles R,et al. Thermally induced emission of light from a metallic diffraction grating mediated by surface plasmons[J]. Optics Communications,1999,168: 117-122.

[4]Marquier F,Joulain K,Mulet J P,et al. Engineering infrared emission properties of silicon in the near field and the far field[J].Optics Communications,2004,237: 379-388.

[5]Marquier F,Laroche M,Carminati R,et al. Anisotropic polarized emission of a doped silicon lamellar grating[J]. Journal of Heat Transfer,2007,129(1): 11-16.

[6]Laroche M,Marquier F,Carminati R,et al. Tailoring silicon radiative properties[J]. Optics Communications,2005,250:316-320.

[7]Marquier F,Joulain K,Mulet J P,et al. Coherent spontaneous emission of light by thermal sources[J]. Physical Review B,2004,69: 155412-155420.

[8]Chen Y B,Zhang Z M. Design of tungsten complex gratings for thermophotovoltaic radiators[J]. Optics Communications,2007,269(2): 411-417.

[9]Tan W C,Sambles J R,Preist T W. Double-period zero-order metal gratings as effective selective absorbers[J]. Physical Review B,2000,61: 13177-13182.

[10]Hibbins A P,Sambles J R,Lawrence C R. Excitations of remarkably nondispersive surface plasmons on a nondiffracting dual-pitch metal grating[J]. Applied Physics Letter,2002,80(13):2410-2420.

[11]Skigin D C,Depine R A. Diffraction by dual-period gratings[J].Applied Optics,2007,46(9): 1385-1391.

[12]Zhang Z M. Nano/Microscale heat transfer[M]. New York:McGraw–Hill,2007: 55-86.

[13]Volz S. Microscale and nanoscale heat transfer[M]. Berlin Heidelberg: Springer–Verlag,2007: 58-97.

[14]Timans P J. Advances in rapid thermal and integrated processing[M]. Dordrecht：Kluwer Academic,1996: 70-125.

[15]Crouse D,Arend M,Zou J P,et al. Numerical modeling of electromagnetic resonance Enhanced Silicon Metal-semiconductor-metal Photodetectors[J]. Optics Express,2006,14(6): 2047-2061.

[16]Taflove A,Hagness S C. Computational electrodynamics: The finite-difference time-domain method[M]. 3rd ed. Boston:Artech House,2005: 230-249.