稳态混合磁体装置低温系统过冷槽的设计与优化

张 倩 欧阳峥嵘 高洪彪 李俊杰

部分符号说明

H:焓值，kJ/kg

MFZ:氦制冷机液化率，L/h;

EX:换热器;

ηs:透平的等熵效率;

QE:换热器换热量，W;

m:氦的质量流量，g/s;

di:换热管内径，m;

do:换热管外径，m;

dm:换热管平均直径，m;

δ:管壁厚，m;

A:换热面积，m2;

L:换热管长度，m;

N:换热管数量;

ρi:管内氦的密度，kg/m3;

μi:管内氦的粘性系数，Pa·s;

cpi:管内氦的比定压热容，kJ/(kg·K);

λi:管内氦的导热系数，W/(m·K);

λo:管外氦的导热系数，W/(m·K);

Δtmax:最大换热温差，K;

Δtmin:最小换热温差，K;

Δt:对数平均换热温差，K;

v:管内氦气流速，m/s;

Gr:格拉晓夫数;

Re:雷诺数;

Pr:管内氦的普朗特数;

Pro:管外氦的普朗特数;

hi:管内传热系数，W/(m2·K);

ho:管外传热系数，W/(m2·K);

h:基于管外的传热系数，W/(m2·K);

V:过冷槽的体积;

t:取液氦的时间，h。

1 引言

稳态强磁场实验装置是中国“十一五”国家大科学工程，由中国科学院合肥物质科学研究院和中国科学技术大学共同承建。其40 T稳态混合磁体由内水冷磁体和外超导磁体组成，其中外超导磁体为11 T，用铌三锡CICC绕制而成，使用4.5 K超临界氦迫流冷却。

为了使通往超导磁体的超临界氦达到温度和流量上的要求，需要在冷箱和超导磁体之间设计一个过冷槽，把从制冷机出来的氦气冷却到4.5 K超临界状态。过冷槽在提供冷量冷却氦气的同时，还为HTS电流引线低温段的冷却提供冷量。本文首先根据制冷机的状态确定了过冷槽进口处的氦气状态，按最大换热面积设计了盘管换热器的大小，并提出阶梯管径理论，根据工程要求对盘管换热器进行了优化，最终确定了过冷槽的大小以及制冷机的工作状态。在本文的设计中，外超导磁体系统的稳态热负荷Q=100 W，通往磁体的超临界氦的质量流量为MF3=18 g/s，制冷机压缩机的最大质量流量为40 g/s，制冷模式下的制冷量为360 W/4.5 K，液化模式下的液化率为110 L/h，当稳态热负荷为100 W时，制冷机工作在混合状态。

2 冷箱进口处氦气状态的确定

图1为氦制冷循环流程图，循环包括液氮冷却级，第一级膨胀冷却级，第二级膨胀冷却级和节流冷却级，两级膨胀机采用串联方式联接，可通过变频装置调节压缩机驱动电机的转速来调节压缩机质量流量。当压缩机以最大质量流量MF1=40 g/s运行时，系统的液化率最大，从制冷机出来的氦气温度最低，所需换热器面积最小;当制冷机的制冷量 Q=100 W，液化率MFZ=0时，压缩机的流量为能维持磁体正常工作的最小流量，此时，从制冷机出来的氦气温度最高，所需换热器面积最大。

图1 氦制冷循环流程图Fig.1 Flow diagram of refrigeration cycle

2.1 压力的选择与确定

螺杆压缩机的排气压力p10=1.3×105Pa，吸气压力略高于大气压，考虑到换热器低压侧的阻力损失，过冷槽的压力选为1.1×105Pa，对应的饱和温度为4.31 K。氮气的排放压力p40也略高于大气压，透平膨胀机得排气压力可根据磁体冷却的压力需要及透平膨胀机的设计限制确定，这里选择5.5×105Pa。

2.2 热平衡计算

对各级换热器进行热平衡分析［1］:

EX6以下的节流冷却:

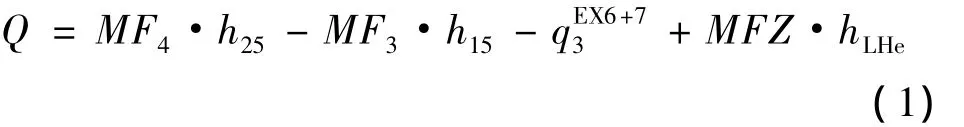
EX7以下:

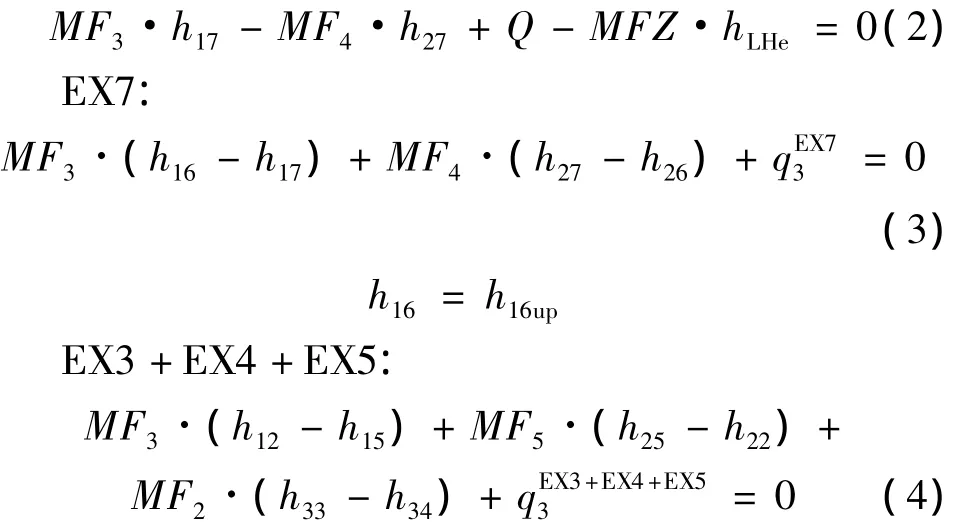
膨胀机等熵效率:

2.3 计算结果

(1)当压缩机以最大质量流量运行时，MF1=40 g/s，T17=6.02 K，MFZ=77.45 L/h。

(2)当压缩机以能维持磁体正常运行时的最小质量流量运行时:MF1=24.84 g/s，T17=6.34 K，MFZ=0。

3 过冷槽的设计计算

过冷槽主要由换热器、液氦杜瓦、各种传感器以及低温传输线构成，其中，换热器为其最主要的部分，因此本文主要针对换热器进行优化从而使过冷槽最优化。由于盘管换热器拥有结构简单、造价低、操作方便，且盘管内可承受高压等优点，所以本文选用盘管换热器作为换热器的设计形式。设计盘管换热器时，要尽可能保证其结构的均匀性，紧凑性与工艺性，且尽可能使各层绕管的长度相等以保证阻力均匀，流体均布［2］，换热管选用导热性能较好的紫铜管。

换热器设计时按照2.3中的情况(2)设计，此时，17点温度最高，所需的换热面积最大，如果换热器的换热量能够满足这种情况，则压缩机在最大流量至最小流量之间任何一个流量工作时，过冷槽都可将制冷机出来的氦气冷却至冷却磁体要求的温度。

3.1 设计思想

氦气在管内流动，随着温度以及压力的下降，氦气的粘性系数会上升，比定压热容和导热系数将会下降，根据公式，随着μ的上升，Re会下降，管内传热系数 hi=0.023Re0.8Pr0.3·，为了保证传热系数不显著减小，需要在压降允许的情况下适当减小管径以保证hi不显著下降。从图2可以看出，当管径不变时，管内传热系数随着温度的下降将会出现明显的下降，当管径随温度呈线性变化时，传热系数减小趋势较为平缓，但在实际应用中，管径不可能随温度呈线性变化，因此，可以选择将管径阶梯式的减小，使其换热能力介于两者之间，以更好的改善换热器的特性，减小换热面积，从而减小换热器的体积。

图2 管内传热系数随温度的变化Fig.2 Change of heat transfer coefficient in tube

3.2 换热器设计计算［3］

换热器换热量的确定:

管内传热系数的计算:管内为强制对流换热，传热系数:

管外传热系数的计算:管外为大空间自然对流换热，传热系数:

基于管外的传热系数计算:

换热面积及管长的确定:

流动阻力的计算:

3.3 换热器计算结果及其优化

过冷槽的主要造价在于影响分配阀箱的花费，因此换热器设计优化的目的是其所占的体积尽可能小，从而减小分配阀箱的体积，进而减小设计制造的费用。为了节省体积，换热管的布置采用换热管相套的方式，细管径的换热管在里面，粗管径的换热管在外面，换热管连接处用接头焊接。

以液化模式下制冷机出口的液氦流速为参考，结合换热管减小有利于换热的理论，初步选定两种换热器模式，模式一是以Ф18 mm×2 mm的紫铜管接制冷机出口，经过一定换热后将工质分为两路，分别选用Ф14 mm×2 mm的换热管相接，每路经过一定换热后，再分为两路，分别接Ф10 mm×1 mm的换热管。模式二在制冷机出口处便将工质分为两路，分别以Ф16 mm×2 mm的换热管相接，经过一定的换热后，将每路工质再分为两路，分别接Ф10 mm×1 mm的换热管。经计算，第一模式的压降为0.16×105Pa，换热器体积为49.37 L，第二种模式的压降为0.087×105Pa，换热器体积为46.72 L。

第二种模式的压降和体积均小于第一种模式，加之在给定的压力条件下，根据工程经验，换热器的压降最好能控制在0.1×105Pa以下，因此换热器的设计选用第二种模式，流道布置如图3，左侧两路为Ф16 mm×2 mm的换热管，右侧4路为Ф10 mm×1 mm的换热管，经过计算求得，盘管换热器的长度为L=0.93 m，盘管分为6层，小管径换热管盘在内层，共4层，大管径换热管盘在外层，共两层，从里到外的盘管直径依次为 D1=0.19 m，D2=0.22 m，D3=0.24 m，D4=0.27 m，D5=0.32 m，D6=0.37 m，盘管换热器所占体积为VE=46.72 L，压降 Δp=0.087×105Pa。盘管换热器三维效果图如图4。

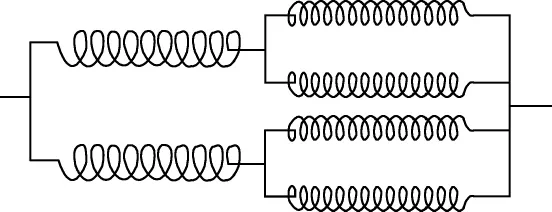
图3 流道布置示意图Fig.3 Runner layout

图4 换热器三维效果图Fig.4 Three-dimensional plot of heat exchanger

3.4 过冷槽的设计计算

制冷机实际工作时，其压缩机流量介于最高流量与最低流量之间，因此，取制冷机实际工作时的液化率为30 L/h，每隔t=15 h从过冷槽中抽取一次液氦转移到液氦杜瓦。过冷槽的体积可分为3部分:换热器体积VE，将换热器完全浸泡所需液氦体积VJ，制冷机在规定时间t内所产生的液氦体积VH，过冷槽的底径为DS，则:

最终计算得到，过冷槽的底径为1.1 m，高度为0.9 m，体积为855 L。

4 结论

过冷槽的设计优化是保证超导磁体能够正常工作的必要条件。首先，必须保证过冷槽的换热量足够大，对制冷机进行两种极限混合模式的计算后选定换热面积最大的一种，使得制冷机的压缩机以任意流量工作时，都可以将氦气降到冷却磁体所要求的温度和压力;其次，对过冷槽最主要的部分换热器进行优化设计，提出阶梯管径理论，在压力允许的范围内最大限度的提高传热系数，减小换热器体积;最后，对过冷槽进行计算，得出过冷槽的相关尺寸以及体积。

1 白红宇，毕延芳.2kW/4K氦制冷机制冷循环的优化计算［J］.真空与低温，2002，8(3):144-148.

2 陈长青，沈裕浩.低温换热器［M］.北京:机械工业出版社，1993.

3 钱颂文.换热器设计手册［M］.北京:化学工业出版社，2002.