液氮流动沸腾数值模拟研究进展

邵雪锋 李祥东 汪荣顺

1 引言

低温流体广泛应用于各种低温换热设备中。在最近几十年里，低温流体的应用领域不断扩展，不仅用作火箭发动机的氧化剂和燃料以及用来冷却超导磁体和电动机，还被用作冷却介质冷却计算机硬件以增加计算速度和微电路密度。和其它低温流体相比，液氮安全，无毒而且廉价，在实验研究中经常被用来代替其它低温介质。因此液氮的利用存在着广阔的前景。由于测试手段有限等原因，液氮流动沸腾的实验条件较为苛刻。早期研究者进行的实验工作［1-3］仅仅关注一些宏观或平均参数来分析低温气液两相流传热，也即拟合实验参数得到换热系数的经验关系式。随着工业技术的快速发展，低温系统对低温流体的换热提出了更高的要求，需要全面了解低温两相流动中的相关参数(温度、压力、流量、流速、含气率，空泡份额等)，因为这些参数的变化直接影响流动的换热与流动状况。传统的经验关系式并不能给出局部参数的变化和分布，需要采用新的方法分析液氮的流动沸腾换热。

随着计算机技术的快速发展，计算能力不断提高，计算流体力学(CFD)技术得以快速发展，并且逐渐发展成为一门比较成熟的学科。作为一种辅助设计和分析的手段，计算流体力学技术已经广泛地应用于各种行业。特别在核能领域，计算流体力学已经成为一种重要的辅助分析手段，到目前为止已经有诸多代码应用于水的两相流动分析中，例如RELAP5、TRAC、CATHARE等。低温流体和以水为代表的高沸点流体的沸腾在本质上有很多类似之处［4］，用于分析水流动沸腾的数学模型理论上也可用来分析液氮的流动沸腾。但是液氮等低温流体的物性不同于高沸点流体，例如，液氮的饱和温度以及接触角要远小于水。物性的差别将会对流动沸腾传热产生影响，不能简单将水的分析结果应用到液氮的流动沸腾分析中。要将CFD技术引入到低温领域，需要针对液氮流动沸腾的特点，建立合适的数学物理模型编制计算程序，并进行大量的实验来验证代码的准确性。只有这样才可准确的分析和预测流动沸腾过程中局部参数的变化和分布，从而用于液氮系统的优化设计和操作。

本文总结和分析液氮流动沸腾时所采用的数值模拟技术，指出这些技术中存在的问题，同时指出一些迫切需要研究的课题，为将最新的数值模拟技术引入液氮流动沸腾分析打下基础。

2 液氮流动沸腾的数值模拟研究现状及存在的问题

由于液氮流动沸腾的实验系统比较复杂，针对液氮流动沸腾进行的实验较为有限，液氮流动沸腾的数值模拟研究则更少。郑正泉［5］采用简化的漂移通量模型来描述管道中的低温气液两相流的流动过程。和一般漂移通量模型中所用的连续方程和动量方程都是动态方程不同，他采用的模型中只有液体连续方程是动态方程，而气相的连续方程以及气相和液相的动量方程都是准平衡态。在该模型中考虑了气体的可压缩性，分析了不同流型，最后比较了相分布以及压力分布的模拟计算结果与实验结果。陆柳柳［6］等采用一维均相流模型对液氮流动过程进行了稳态数值模拟，得到了循环流动过程中液氮含气率、压力和温度沿管程方向的分布情况，并对由于不同回路条件引起的不同结果进行了分析。Ishimoto［7］等采用基于非稳态漂移通量模型的控制方程描述了垂直通道内液氮流动沸腾的传热过程，详细分析了液氮沸腾两相流动中的二维结构。孙淑风［8］采用分相流动模型环行通道内的环状流进行了数值模拟，该模型基于守衡定律，得到了液膜中的压力梯度，传热系数速度以及温度分布。传热系数的实验值比计算结果偏高30%。上述研究者分别采用不同的数学模型针对液氮流动沸腾进行了数值模拟研究。他们都将数值模拟结果和实验结果进行了比。通过比较表明这些数学模型在一定程度上可用于分析液氮的流动沸腾，证明了数值模拟方法可以作为实验方法的一种补充。除Ishimoto外，其它研究者只给出空泡系数沿管程的分布，并未给出局部参数变化情况以及详细空间分布。表明这些研究者所采用的数学模型不能更深入的研究液氮的流动沸腾以获的局部参数。李祥东［9-14］将两流体模型引入到低温流体的沸腾流动分析中。他采用两流体模型和CFD技术作为液氮流动沸腾过程研究的框架，根据实验观测结果建立适当的封闭方程，然后利用得到的理论模型实现对双流体模型的修正和完善，同时借助CFD技术实现对垂直通道内液氮流动沸腾过程的预测。他的研究建立了液氮核态沸腾壁面上的传热传质机理模型及流场内的相间传输模型，并采用以上模型作为封闭方程完成了对双流体模型的初步修正，数值模拟的结果与实验数据在一定范围内吻合较好。

从上面可以看出，到目前为止只有少量的研究者采用有限的数学模型分析了液氮的流动沸腾。只有Ishimoto和李祥东分别采用漂移通量模型和两流体模型得到液氮流场中局部参数的详细分布。漂移通量模型没有完全考虑到气液两相间的相互作用，和两流体模型相比，它忽略了气液两相间传输的局部特征，一般被看作是一种简化的两流体模型。和均相模型以及分相模型相比，两流体模型可以获得更为详细和准确的预测结果。将两流体模型引入低温流体的分析是一个很大的进步。但到目前为止两流体模型仅用于分析泡状流。并没有研究者采用两流体模型分析液氮流动沸腾中出现的其它流型或流型过渡区。在实际的低温系统中，例如汽化器，液氮的流动沸腾过程中包括多种流型。如果采用传统的设计方式(先根据流型判断准则判断并确定各流型，之后再针对各流型采用经验关系式)，将带来两步误差。

计算流体力学大师Patankar［15］指出，理论的预测出自一个数学模型的结果，而不是出自于一个实际的物理模型。准确的模拟液氮流动沸腾中的流型转变区需要考虑各影响因素，建立准确的数学模型。已经有不少研究者采用数值模拟的方法研究水流动沸腾流型转变区，但国内外几乎没有关于液氮沸腾流型转变区的数值模拟研究，因此需要借鉴水的流动沸腾数学模型，根据液氮的特点建立准确的封闭方程。在液氮泡弹状流型过渡区，明显的存在着气泡破裂和聚合等现象，在两流体模型中考虑气泡的破裂和聚合现象，将大大拓展两流体模型的使用范围。

3 可用于液氮流动沸腾数值模拟研究的数学模型

在两相流中，最重要的基本几何参数是空泡系数，相界面面积浓度，当地气泡尺寸。空泡系数表征气液相的分布，它是换热系统中热流体设计的必需参数。两流体模型中的很多参数，比如气相在过冷液相中的冷凝速度，相间曳力等是相界面面积浓度或当地气泡尺寸的函数，因此相界面面积浓度和当地气泡尺寸强烈的影响相间的动量、质量和能量传输，是两流体模型中的必需参数。在目前的两流体模型中，当地气泡尺寸通常由经验关系式确定，相界面面积浓度则由空泡系数和当地气泡尺寸的关系得到。因此，准确的确定当地气泡尺寸显得格外重要。Tu等［16］采用两流体模型分析低压水流动沸腾，发现数值模拟得到的径向当量气泡直径以及气液相速度分布与实验结果存在较大偏差。这是因为在两流体模型中，过冷液体中关于气泡尺寸的经验关系式只能用来预测宏观沸腾现象，并不能用它们准确的预测实验中可以观察到的气泡聚合和破裂等微观现象。为了更准确的模拟液氮流动沸腾，需要考虑气泡之间的相互作用以建立更为准确的气泡直径分布函数。也即需要在两流体模型的基础上建立一个关于气泡直径或者相界面面积浓度的补充方程，在这个补充方程中考虑气泡的破裂和聚合等因素，从而完善两流体模型。群体平衡模型的成熟为补充方程的建立奠定了基础。

群体平衡模型描述的是系统中某些实体的数量的平衡关系，对于不同的系统，实体可以是固体颗粒、液滴、气泡或者细胞等。对于沸腾两相流系统，这些实体就是流场中的气泡。对于某一给定的气液两相流空间，除了不断有气泡进入或离开该空间外，空间内的气泡还会由于各种原因(如聚合、破裂以及相变等)不断产生或消亡。大量的研究者基于群体平衡模型建立了两流体模型的补充方程，这些补充方程可分为3类:

第一类补充方程将相界面面积浓度作为一种传输量，根据气泡数量密度和相界面面积浓度的关系建立相界面面积传输方程，在相界面面积方程的源项中考虑气泡破裂和聚合等因素。Ishii等［17］认为由于两相流动中存在较多的可变形的移动界面，相间传输机理比较复杂，因此，两流体模型中最大的不足是很难准确的封闭相间传输项。相间传输项和相界面面积浓度以及驱动力成正比。驱动力则取决于局部传输机理，包括相界面附近的湍流等。因此，相界面面积浓度是一个必需的量。

第二类补充方程根据气泡直径的大小将气泡分为若干组(N组)，通过气泡数量密度和气泡尺寸的关系将群体平衡模型与两流体模型结合起来，可在较大范围预测两相流场内的气泡直径分布。这类方程组(称为多尺寸组方程)中需要计算每组气泡的连续方程，液相的连续方程以及气液相的动量和能量方程与两流体模型并无区别。在气泡的连续方程中可以考虑气泡的破裂和聚合。Tu等采用此类方程模拟了低压水的过冷流动沸腾，数值模拟结果和实验结果吻合的较好。

第三类补充方程将平均气泡体积作为传输量，基于群体平衡模型建立了平均气泡体积的传输方程。Lehr等［18］采用该类补充方程分析了鼓泡床中的气泡特征。

3类补充方程都可以考虑气泡之间的相互作用，可被用于分析流型转变区域。加入此类补充方程将使得两流体模型的使用范围大大拓展。前两种方法都被认为是研究两相流动有前途的方法，第三类方法也引起了一些研究者的注意。国内外学者针对水的流动沸腾进行了广泛而深入的研究，相界面传输方程和多尺寸方程得到了广泛的关注。但是国内外很少有研究者将这些模型引入到低温流体的流动沸腾中。准确数学模型的缺乏限制了数值模拟技术在液氮流动沸腾中的应用，因此，在低温领域中引入这些数学模型是必需的。李祥东成功的将两流体模型引入到液氮的流动沸腾分析表明准确的数学模型是数值模拟成功的基础。关于水的实验证明两流体模型并非完全的机理模型，需要针对液氮流动沸腾的特点建立准确的补充方程从而完善两流体模型。

4 液氮流动沸腾数值模拟研究展望

由于液氮的物性和水存在着较大的区别，液氮的流动沸腾过程中存在着更加复杂的问题。这些问题包括液氮两相流动中存在较多可变形的移动界面，以及液氮物性的不连续性和气液界面处存在着复杂流场等。使得准确建立液氮流动沸腾的数学模型并不容易。

Ishii指出在两相流动中，至少有4种尺度是非常重要的。这4种尺度包括系统尺度、连续介质假设所要求的宏观尺度、局部结构所要求的中等尺度和分子结构有关的微观尺度。其中系统尺度主要关注系统的瞬态效应以及组件的相互作用，宏观尺度包括相界面结构以及质量、动量和能量的传输，中等尺度强调湍流对动量和能量的影响以及相界面处质量、动量和能量的传输。要准确的采用数值模拟方法预测液氮的流动沸腾，需要在这4种尺度上进行广泛而深入的研究。相界面传输方程和多尺寸组方程所考虑的气泡聚合和破裂现象属于微观度，需要深入和集中的研究。和多尺寸组方程相比，相界面传输方程求解的只是相同控制容积中基于平均分布的相界面面积和空泡系数得到的平均气泡尺寸，因此相界面面积方程可看作是多尺寸组方程的简化形式。完善两流体模型的第一步工作是将多尺寸组方程引入到液氮的流动沸腾分析中，因为准确分析流场中气泡尺寸的分布是建立准确相间传输模型的基础。在多尺寸组方程中，壁面传热传质模型依然是求解成功与否的关键模型之一。李祥东的研究表明，竖直通道内液氮流动沸腾中的活化核心密度，气泡脱离频率可分别采用Kirichenko［19］，Cole［20］提出的公式计算。气泡脱离直径则可采用Kirichenko［21］提出的公式。数值模拟中采用这类经验关系式得到的数据可在一定范围内与实验数据吻合较好。但为了拓展两流体模型的使用范围和增加两流体模型的预测精度，需要采用更加机理的方法减少经验关系式带来的不确定性，这需要详细的研究气泡的核化，生长，滑移和脱离。因此，完善两流体模型的第二步工作是准确的建立液氮流动沸腾中气泡的受力分析模型，得到准确的气泡脱离直径公式和气泡脱离频率公式。另外目前两流体模型中的壁面热量拆分模型只适合于气泡迅速离开加热壁面的过冷沸腾，该模型中并未考虑气泡的滑移，第三步工作需要修正目前两流体模型中的壁面热量拆分模型。

目前，第一部分工作已初步完成。本文针对几何原型为一内径6 mm，外径20 mm，长1.5 m的竖直环行管道进行了数值计算。过冷度为5 K的液氮从环形通道下部垂直向上流动，入口的液相速度为0.144 m/s;内壁均匀加热，加热量为18 000 W/m2;出口压力为0.7 MPa。由于壁面热流量均一，为了充分利用环形几何形状，只将其1/4作为模拟区域。采用适体网格系统在环形通道中产生三维网格，最后得到总14(径向)×30(高度)×3(沿周长方向)个控制容积。活化核心密度，气泡脱离频率分别采Kirichenko，Cole提出的公式计算，气泡脱离直径则可采用Kirichenko提出的公式。

图1给出了3个轴向位置的平均当量气泡直径的径向分布，从数值模拟的结果可以看出，当量气泡直径的最大值出现在管道中而不是加热壁面附近，数值分析的结果与液氮流动沸腾的可视化实验相符。沿流动方向，当量平均气泡直径的最大位置慢慢趋近于管道中央。在出口处最大气泡直径出现在管道正中间，表明此时在管道中间形成了大的弹状气泡。

图1 平均当量气泡直径的径向分布Fig.1 Local mean radial profiles of Sauter diameter at different height

图2 给出了空泡系数径向分布，在高度为0.925 m处，空泡系数的最大值出现在加热壁面，沿流动方向空泡系数的最大值渐渐远离加热壁面，接近出口处时最大空泡系数出现在管道中间，同样表明此时流动处于弹状流状态。

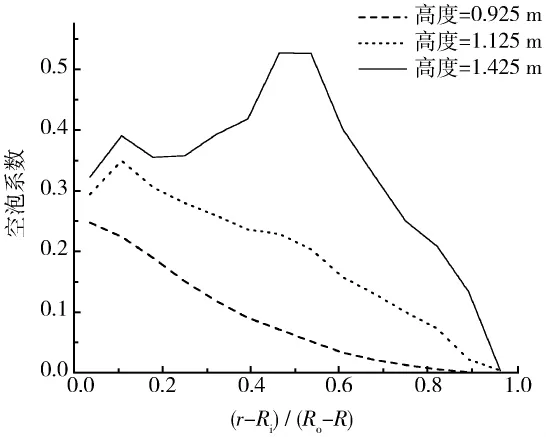
图2 空泡系数的径向分布Fig.2 Local mean radial profiles of void fraction at different height

图3 和图4给出了沿流动方向分布的平均当量气泡直径和空泡系数的分布。从图3可以看出，在某一轴向位置平均当量气泡直径开始超过气泡起飞直径，此后气泡的聚合作用越来越明显，形成较大的气泡，直到接近出口处产生弹状气泡。图4的空泡系数分布可以看出，沿着流动方向，刚开始空泡系数的增长速度较平缓，到某一位置时，空泡系数的增长速度急剧增加。该结果符合过冷流动沸腾的特点。

图3 平均当量气泡直径沿流动方向的分布Fig.3 Axial distribution of mean Sauter diameter

图4 空泡系数沿流动方向的变化Fig.4 Axial distribution of mean void fraction

这4个图表明多尺寸方程可以通过气泡尺寸和空泡系数的变化和分布捕捉到气泡破裂和聚合的相关信息，还可以判断流动沸腾处于何种流型，因此多尺寸组方程可以扩展两流体模型的使用范围。

5 结语

只有少量的研究者采用数值模拟的方法研究了液氮的流动沸腾，只有Ishimoto和李祥东得到了液氮流场中局部参数的详细分布。Ishimoto的方法中忽略了气液两相间传输的局部特征，两流体模型中的气泡直径分布采用经验关系式，这些因素限制了漂移通量模型和两流体模型的使用范围。拓展两流体模型的范围需要考虑流场中气泡的破裂和聚合因素。数量密度方程的成熟为两流体模型的完善奠定了基础。建立在数量密度基础上的相界面传输方程和多尺寸组方程被认为是很有前途的研究两相流的方法，受到了广泛的关注。将这些模型引入到低温流体的沸腾分析中，可以更为准确的分析流场中的局部数据，判断流型转变。从而可以辅助低温换热设备的设计与分析。

相界面传输方程只是多尺寸组方程的一种简化形式，因此，完善两流体模型需要首先将多尺寸组方程引入到低温流体的沸腾分析中。两流体模型中，核态沸腾壁面传热传质模型需要继续加以完善，建立更为机理的气泡起飞直径公式和气泡脱离频率公式。同时需要考虑气泡的滑移进一步改善壁面热量拆分模型。本文已经初步完成第一步工作，即将多尺寸组方程引入到液氮的流动沸腾分析中。结果表明多尺寸组方程能考虑实验观察到的气泡破裂和聚合现象，并且能对流型转变区域进行模拟。低温流体流动沸腾的实验数据相当有限，需要进行更多的实验获的准确的局部数据，进一步修正气泡起飞直径，气泡脱离频率等公式，从而验证代码的可靠性。

1 Klimenko V V.Heat transfer intensity at forced flow boiling of cryogenic liquids in tubes［J］.Cryogenics，1982，22(6):569-576.

2 Steiner D，Schlunder E U.Heat transfer and pressure drop for boiling nitrogen flowing in a horizontal tube1saturated flow boiling［J］.Cryogenics，1976，16(3):387-399.

3 Steiner D，Schlunder E U.Heat transfer and pressure drop for boiling nitrogen flowing in a horizontal tube2.saturated flow boiling［J］.Cryogenics，1976，16(3):457-764.

4 Barron R F.Cryogenic Heat Transfer［M］.Taylor＆Francis，Philadelphia，1999.

5 郑正泉.低温汽液两相流动态模拟及实验研究［J］.低温与超导，1999，27(4):21-26.

6 陆柳柳，匡 波，陈 宏.低温气液两相流数值计算［J］.低温与超导，2005，33(1):27-31.

7 Ishimoto J，Oike M，Kamijo K.Two-dimensional numerical simulation of boiling two-phase flow of liquid nitrogen［J］.Transactions of the Japan Society for Aeronautical and Space Sciences，2000，43(141):114-121.

8 Chen L F，Wu Y Y，Liu Y Z，et al..The study on performance of heat transfer in a quasi-annular flow condenser-evaporator［J］.Cryogenics，1999，39(3):209-216.

9 李祥东，汪荣顺，石玉美.垂直通道内低温液体过冷流动沸腾传热的数值预测模型［J］.低温工程，2006，34(1):6-11.

10 李祥东.竖直通道内液氮流动沸腾的双流体模型及沸腾两相流不稳定性研究［D］.上海:上海交通大学大学，2007.

11 李祥东，汪荣顺，石玉美.低温液体核态流动沸腾传热的机理模型［J］.低温与超导，2006，34(3)，168-171.

12 Li X D，Wang R S，Gu A Z.Numerical simulation of flow boiling of cryogenic liquids in tubes［C］.In:20th International Cryogenic Engineering Conference，Beijing，2004.

13 李祥东，汪荣顺，顾安忠.低温液体流动沸腾数值计算中的动量模拟［J］.低温与超导，2004，32(4):53-58.

14 李祥东，汪荣顺，顾安忠.低温液体流动沸腾数值计算中的相间传热模型［J］.低温与超导，2005，33(2):26-29.

15 Patankar SV.Numerical heat transfer and fluid flow［M］.McGraw:McGraw-Hill，1980.

16 Yeoh G Y，Tu JY.Population balance modeling for bubbly flows with heat and mass transfer［J］.Chemical Engineering Science，2004，59(15):3125-3139.

17 Ishiii M，Hibiki T.Thermo-fluid dynamics of two-phase flow［M］.Springer，New York，2006.

18 Lehr F，Mewes D.A transport equation for the interfacial area density applied to bubble columns［J］.Chemical Engineering Science，2001，56(3):1159-1166.

19 Kirichenko Y A，Dolgoy M L，Levchenko N M.A study of the boiling of cryogenic liquids［J］.Heat Transfer-Soviet Research，1976，8(4):63-72.

20 Cole R.A photographic study of pool boiling in the region of the critical heat flux［J］.AIChE Journal，1960，6(3):533-542.

21 Kirichenko Y A，Slobozhanin L A，Shcherbakova N S.Analysis of quasi-static conditions of boiling onset and bubble departure［J］.Cryogenics，1983，23(2):110-112.