AGNES算法在K-means算法中的应用*

周爱武，潘 勇，崔丹丹，肖 云

(安徽大学 计算机科学与技术学院，安徽 合肥 230039)

K-means算法是基于划分的经典聚类算法，该算法简单、快速，得到了广泛应用，但是该算法对孤立点是敏感的，其次该算法要求用户必须事先给出簇数k值，该算法聚类结果受初始聚类中心随机性选择影响比较大，聚类中心选择不当，容易导致聚类准确度下降，甚至无法得到聚类结果。针对以上缺点，国内外许多专家和学者提出很多对K-means算法的改进，比如参考文献[1]~参考文献[3]是基于密度的对K-means算法进行改进来找到密度比较高的代表点作为初始聚类中心，参考文献[4]是把遗传算法应用到K-means算法中来确定k个初始聚类中心，这种结合能够进行一种全局优化，可提高算法的准确率，将智能算法与K-means算法的结合也是近年来研究的热点。K-means算法以及其改进的算法已经应用到了各个领域，取得了很好的效果，比如参考文献[3]是改进的K-means算法在客户划分中的应用，参考文献[5]是在图像标注和检索的应用，参考文献[6]是在存在异常孤立点大数据集中进行聚类发现簇的应用。由此可见，K-means算法的效率高、时间复杂度低，应用前景宽广。

本文针对初始聚类中心随机选择这个缺陷，提出将凝聚层次聚类算法AGNES应用到改进的算法中，得到k个密度比较高的初始聚类中心，并将其应用到K-means中去进行聚类。实验表明，改进的算法运行效率高，并能获得比较高的准确率。

1 算法的基本思想

1.1 K-means算法

算法接收输入量k，然后将n个数据对象划分为k个聚类以便使得所获得的聚类满足：同一聚类中的对象相似度较高；而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“聚类中心对象”来进行计算的。

K-means算法步骤描述如下：

输入：n个数据对象，簇数k

输出：k个簇的集合。

(1)从n个数据对象中任意选择k个数据对象作为初始聚类中心。

(2)根据簇中数据对象的平均值，将每个数据对象依次划分到最近距离聚类中心标志的簇中。

(5)如果E值变化明显，将返回步骤(2)。

1.2 AGNES算法

[7]中提到的AGNES算法是凝聚的层次聚类方法。AGNES算法最初将每个对象作为一个簇，然后这些簇根据某些准则被一步步地合并。

AGNES算法描述如下：

输入：包含n个数据对象的数据库，终止条件簇的数目 c；

输出：c个簇，达到终止条件规定簇数目。

(1)将每个数据对象当成一个初始簇；

(2)REPEAT；

(3)根据两个簇中最近的数据点找到最近的两个簇；

(4)合并两个簇，生成新的簇的集合；

(5)UNTIL达到定义的簇的数目；

2 改进K-means算法

K-means算法初始聚类中心是随机选取的，选取不当的话，将会无法得到正确的聚类结果。而AGNES算法将最近的数据对象聚集在一起形成簇，根据AGNES算法的这种思想，提出一种新的算法来确定k个初始聚类中心。

2.1 相关概念

定义1欧式距离

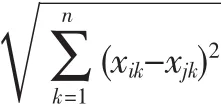
定义2点的密度

数据xi和距离α，以xi为圆心，α为半径的区域内对象的个数 (包括圆心自身)记为该对象的密度，记为Density(xi)=(p 的 个 数|Distance(xi，p)≤α)， 其 中 Dis tan ce(.)为欧式距离，α取所有数据对象间距离和的平均值。

定义3平均密度

2.2 初始聚类中心的确定算法

Initial Clustering Center算法如下：

输入：n个数据对象的数据集 DataSet，聚类簇数k，参 数 θ，ClusterSet、HighSet、CenterSet 3 个 集 合 开 始 均 为空。

输出：k个初始聚类中心数据集CenterSet。

(1)将每个对象当成一个初始簇；

(2)REPEAT；

(3)根据两个簇中最近的的数据点找到最近的两个簇；

(4)合并两个簇，生成新的簇的集合；

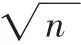
(6)计算数据对象的平均密度Ave；

(7)对步骤(5)中生成的c个簇将其加入到ClusterSet集合中，分别计算每个簇中数据对象的个数，将个数大于Ave的簇加入到HighSet集合中；

(8)令 i=1；

(9)如果HighSet集合不为空，执行步骤 (10)~步骤(13)；否则执行步骤(15)~步骤(18)；

(10)REPEAT；

(11)取出HighSet集合中数据对象个数最多的簇cx；

(12)计算该簇cx中数据对象的平均值做为第i个初始聚类中心，将其加入到CenterSet集合中去，并将簇cx从 HighSet和 ClusterSet中删除，i=i+1；

(13)UNTIL得到k个初始聚类中心；

(14)如果步骤(10)~步骤(13)生成的初始聚类中心个数小于k，并且HighSet集合为空，即执行步骤(15)~步骤(18)；

(15)REPEAT；

(16)取出ClusterSet集合中数据个数最多的簇cx；

(17)计算簇cx中数据对象的平均值做为第i个初始聚类中心，将其加入到 CenterSet集合中去，并将簇cx从ClusterSet中删除，i=i+1；

(18)UNTIL得到k个初始聚类中心；

(19)算法结束。

2.3 改进的K-means算法

改进K-means算法如下：

(1)运行 Initial Clustering Center算法，得到 k个初始聚类中心集合CenterSet；

(2)输入 k值、k个初始聚类中心集合 CenterSet和数据对象集合DataSet；

(3)运行K-means算法，输出K个聚类，算法结束。

3 改进后的实验及分析

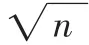
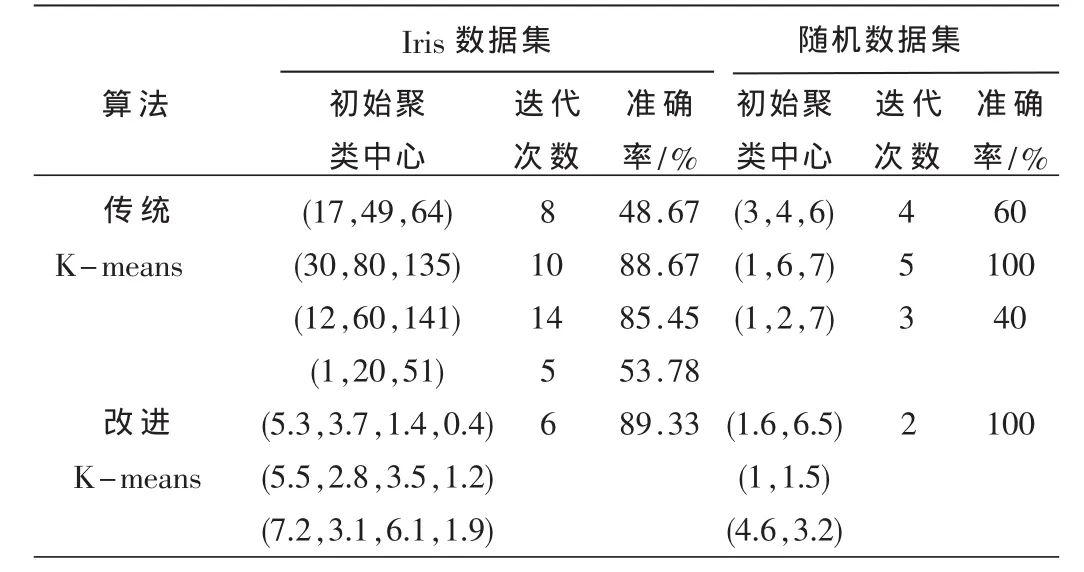
表1 传统K-means算法和改进K-means算法的比较

从表1 Iris数据集可以看出传统K-means算法的迭代次数有时比改进K-means算法要小，但是其准确率却显得很低。这说明K-means算法受初始聚类中心的影响比较大，一旦选择不当，准确率将会很低，而优化的初始聚类中心是比较稳定的，符合数据对象的实际分布，同时可以尽快收敛最优解并且准确率高。从随机数据集整体上来看，改进的K-means算法的迭代次数减少，收敛速度比较快，准确率很高。所以改进的K-means算法收敛速度比较快，得到的初始聚类中心符合数据对象的实际分布，提高了聚类准确率，达到了更好的聚类效果，同时该算法在烟草配送点分配问题等领域都得到了很好的应用。

本文结合层次聚类算法AGNES算法，提出一种确定初始聚类中心的算法，使得到的初始聚类中心比较稳定，符合数据的实际分布，避免选到孤立点，大大提高了算法的准确率和效率。同时改进的算法一个优点是能进行异常点的发现，能够对网络异常进行检测。但是改进K-means算法的时间复杂度不如传统K-means算法，所以今后的研究方向主要是针对大数据集在时间复杂度的提高上作进一步的研究，并将改进的算法应用到其他实际领域中。

参考文献

[1]赖玉霞，刘建平.K-means算法的初始聚类中心的优化[J].计算机工程与应用，2008，44(10)：147-149.

[2]刘艳丽，刘希云.一种基于密度的 K-均值算法[J].计算机工程与应用，2007，43(32)：153-154.

[3]向坚持，刘相滨，资武成.基于密度的 K-Means算法及在客户细分中的应用研究 [J].计算机工程与应用，2008，44(35)：246-248.

[4]孙秀娟，刘希玉.基于初始中心优化的遗传K-means聚类新算法[J].计算机工程与应用，2008，44(23)：166-168.

[5]潘崇，朱红斌.改进K-means算法在图像标注和检索中的应用[J].计算机工程与应用，2010，46(4)：183-185.

[6]ESTER M，RIEGEL H P.A density based algorithm for discovering clusters in large spatial databases with noise[C].Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining(KDD-96)， Ortland，Oregon，1996.

[7]毛国君，段立娟，王实，等.数据挖掘原理与算法[M].北京：清华大学出版社，2000年.