风电机组变桨距功率简化计算方法
周正叶,洪荣晶,高学海,王学辉
(1.南京工业大学 机电一体化研究所,南京 210009;2.上海欧际柯特回转支承有限公司,上海 201906)
在风电技术迅猛发展的今天,变桨距型风力发电机由于有较高的风能利用率,较好的启动和制动性能并且在机组脱网时不需经历突甩负载过程等优点,得到了广泛的应用。变桨距技术已是当今风电机组普遍采用的技术。目前风电机组变桨距机构的驱动方式有液压驱动和电动机驱动两种。由于电动机驱动结构简单,精度高,能进行独立变桨距,因此受到了很多厂家的青睐。现在有关变桨距系统的研究文献很多,多数是对变桨距系统控制方法的研究[1-3],也有部分是对变桨距力矩计算方法的研究[4-7]。下文以电动机驱动的变桨距系统为研究对象,提出了一种变桨距驱动功率的简化计算方法,为变桨距系统的设计和部件选型提供参考。
1 变桨距传动系统
图1所示为一种由电动机驱动的变桨距传动系统。其工作原理为:当变桨距控制器发出变桨距控制指令后,驱动电动机输出转矩,经过传动轴和减速箱,最后由小齿轮传递至变桨轴承内齿圈上,从而带动变桨轴承的内圈与叶片一起旋转,实现了改变桨叶节距角(以下简称桨距角)的目的,桨距角的实际变化值由位置传感器测定并进行反馈,实现闭环控制。
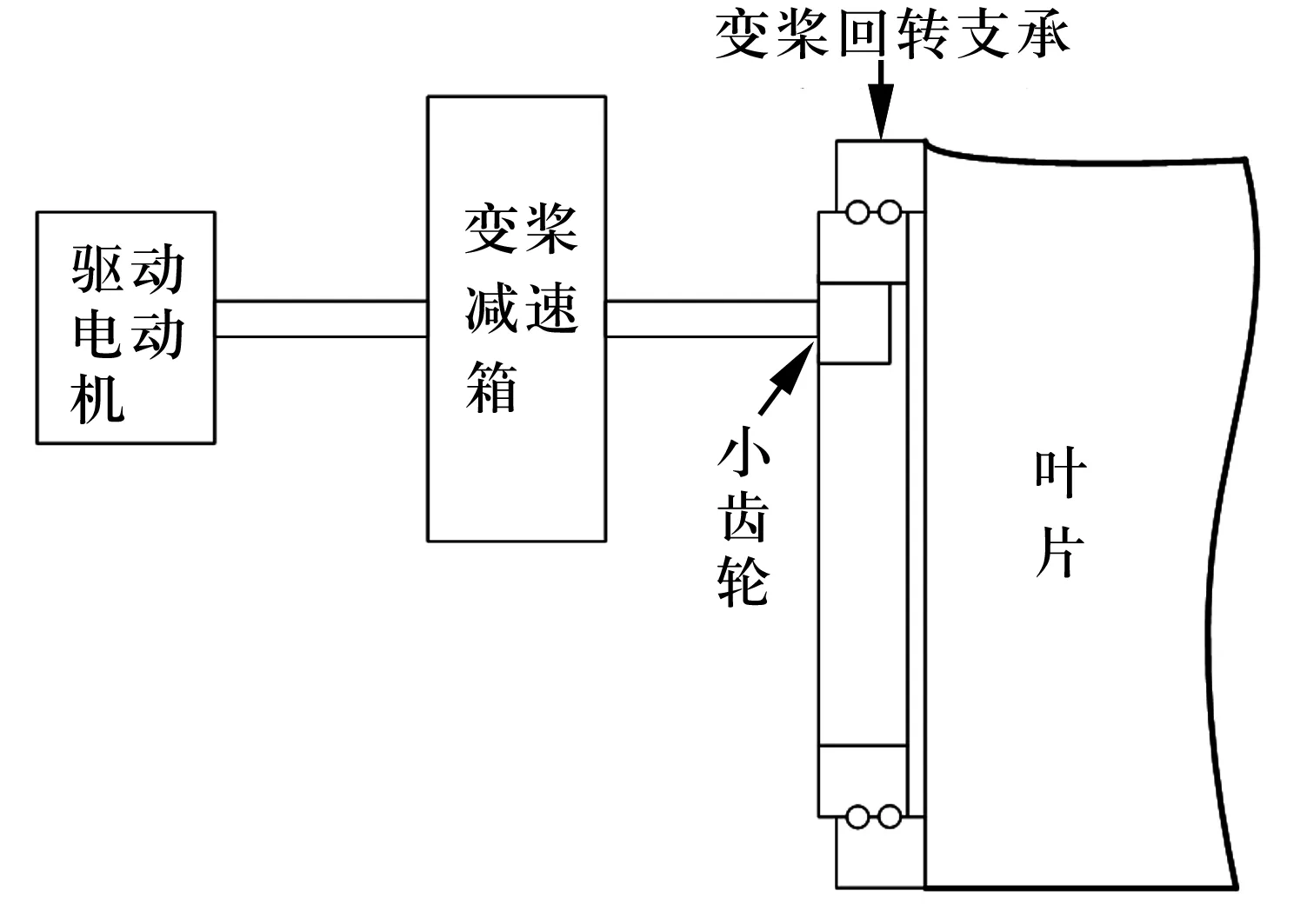
图1 变桨距系统
设电动机输出转矩为TN,叶片上产生的变桨距力矩为T,则
P=aTNωm,
(1)
T=jηcTN,
(2)
式中:P为驱动总功率;ωm为电动机转速;a为安全系数;j为总减速比,j=ωm/ωpitch,ωpitch为变桨角速度;ηc为机构总传递效率。
在叶片变桨距过程中, 变桨距力矩T为[4]
T=Tc+Ta+Tm+Tg+Tf+Te,
(3)
式中:Tc为桨叶离心力产生的变桨阻力矩;Ta为作用在桨叶上的空气动力变桨阻力矩;Tm为桨叶绕其纵轴变桨产生的惯性力矩;Tg为桨叶重心偏离纵轴产生的力矩;Tf为运动副摩擦阻力矩(主要指变桨轴承力矩);Te为弹性变形引起的力矩。
由于Tm,Tg,Te相对于其他力矩很小,可以忽略,这里仅需考虑Tc,Ta,Tf即可。
2 变桨距力矩计算
2.1 桨叶离心力产生的变桨阻力矩
由文献[5-6]可得由桨叶离心力引起的惯性力矩为
(4)
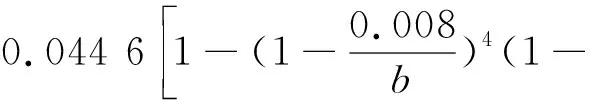

式中:ρb为叶片密度;ω为风轮角速度;Jmax,Jmin分别为叶片截面最大、最小惯性矩;β为扭角;dr为每段桨叶长度;b为半径r处叶片截面弦长;c为叶片截面厚度;D为叶轮直径。
为便于数值计算,将整个叶片离散成各小段,即
(5)
2.2 空气动力产生的变桨阻力矩
如图2所示,当气流经过叶片时,叶片上方气流速度增加,压力下降,叶片下方的气流压力基本维持原来状态不变,于是叶片会受到向上的作用力F。

图2 桨叶在空气动力下的受力
合力F作用在风机叶片上,对变桨纵轴产生扭矩。此时如果变桨使得桨距角增大,则该力引起变桨阻力矩;如果变桨使得桨距角减小,则该力有助于减小变桨驱动力矩。F可以分解为升力Fl和阻力Fd[7]。
(6)
式中:ρ为空气密度,kg/m3;v为吹向叶片的风速,m/s;b为半径r处叶片弦长,m;dc为叶素厚度,m;Cl,Cd分别为升力系数和阻力系数,取决于叶片的叶形,可由叶片生产厂家提供或标准叶型手册查得。
升力dFl和阻力dFd的合力dF为
假设变桨纵轴距叶片前缘距离为Xd,空气动力合力F距叶片前缘为Xf,则有
dTa=(Xf-Xd)dF。
(7)
对于整个叶片而言,由空气动力引起的变桨距力矩为
(8)
用解析法求解(8)式是比较困难的,为了便于数值计算,将整个叶片离散成各个小段,即
(9)
2.3 运动副摩擦阻力矩
运动副摩擦阻力矩主要指变桨回转支承摩擦阻力矩。 建立力学分量坐标如图3所示,以变桨纵轴为z轴,以变桨回转支承的径向且与轮毂旋转中心轴平行的方向为x轴,以变桨回转支承的另一径向且与x轴垂直的方向为y轴。 由文献[8]可知,变桨轴承的摩擦力矩为
(10)
(11)
(12)
Fzb=G+Fgcosφ,
(13)
式中:Mxy为变桨回转支承在x-y平面内受到的总倾覆力矩,是Mxb与Myb的矢量和;Fzb为变桨回转支承受到的轴向力;Fxy为变桨回转支承所受到的总径向力,是Fxb与Fyb的矢量和;μ为摩擦系数;Dpw为滚子组节圆直径;G为叶片重力;Fg为叶片旋转时的离心力;φ为桨叶纵轴线与重力方向的夹角。
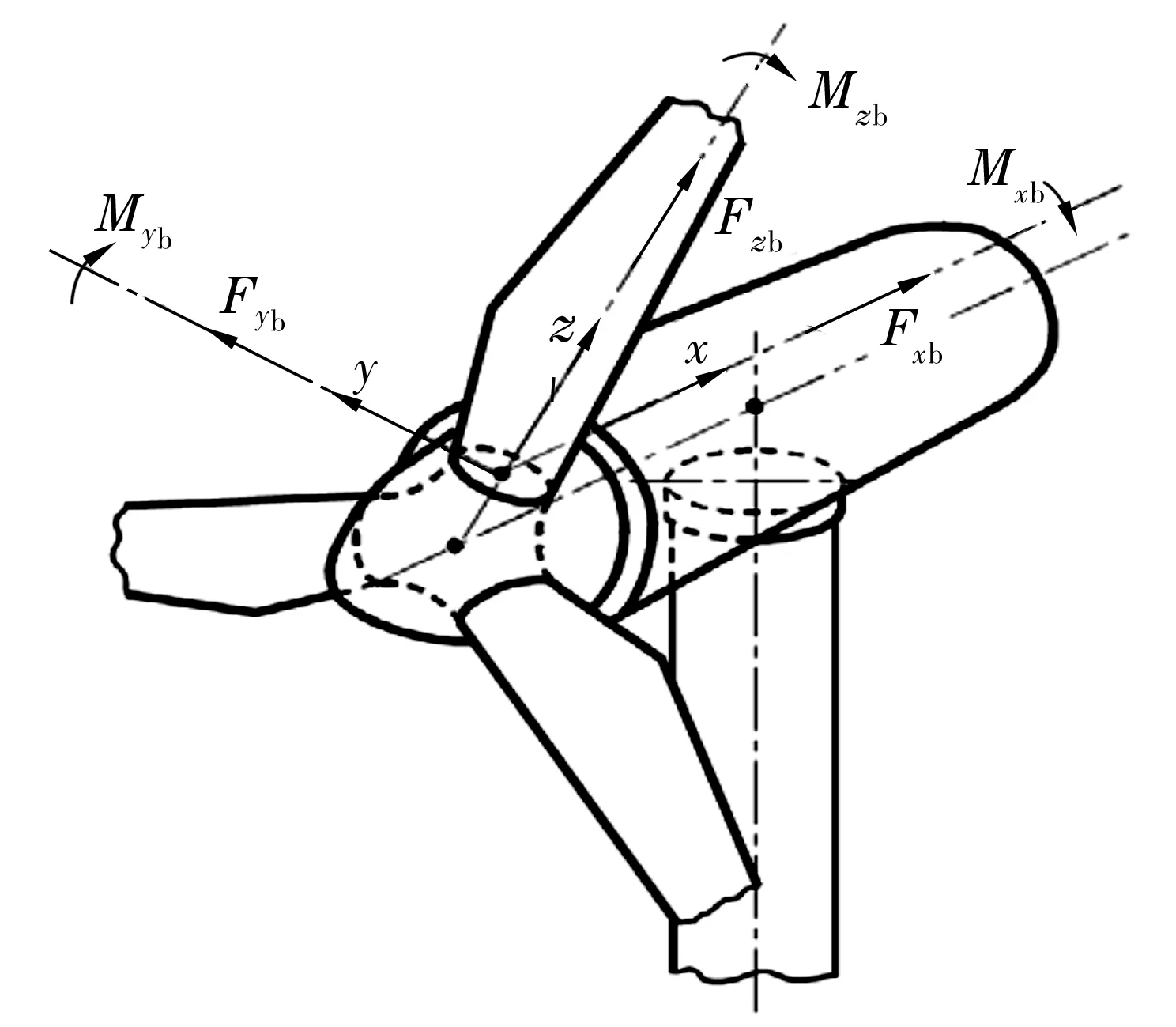
图3 力学分量坐标系
为计算各力学分量,建立如图4所示叶轮流场模型。 其中U,V1,V2分别为来流风速、通过风轮桨叶平面的风速和桨叶平面后部尾流内的风速。根据贝兹理论,最大有59%的风能理论上可以转化为叶轮转动的机械能,假设风机在风速U下的实际风能利用效率为ηs,则有
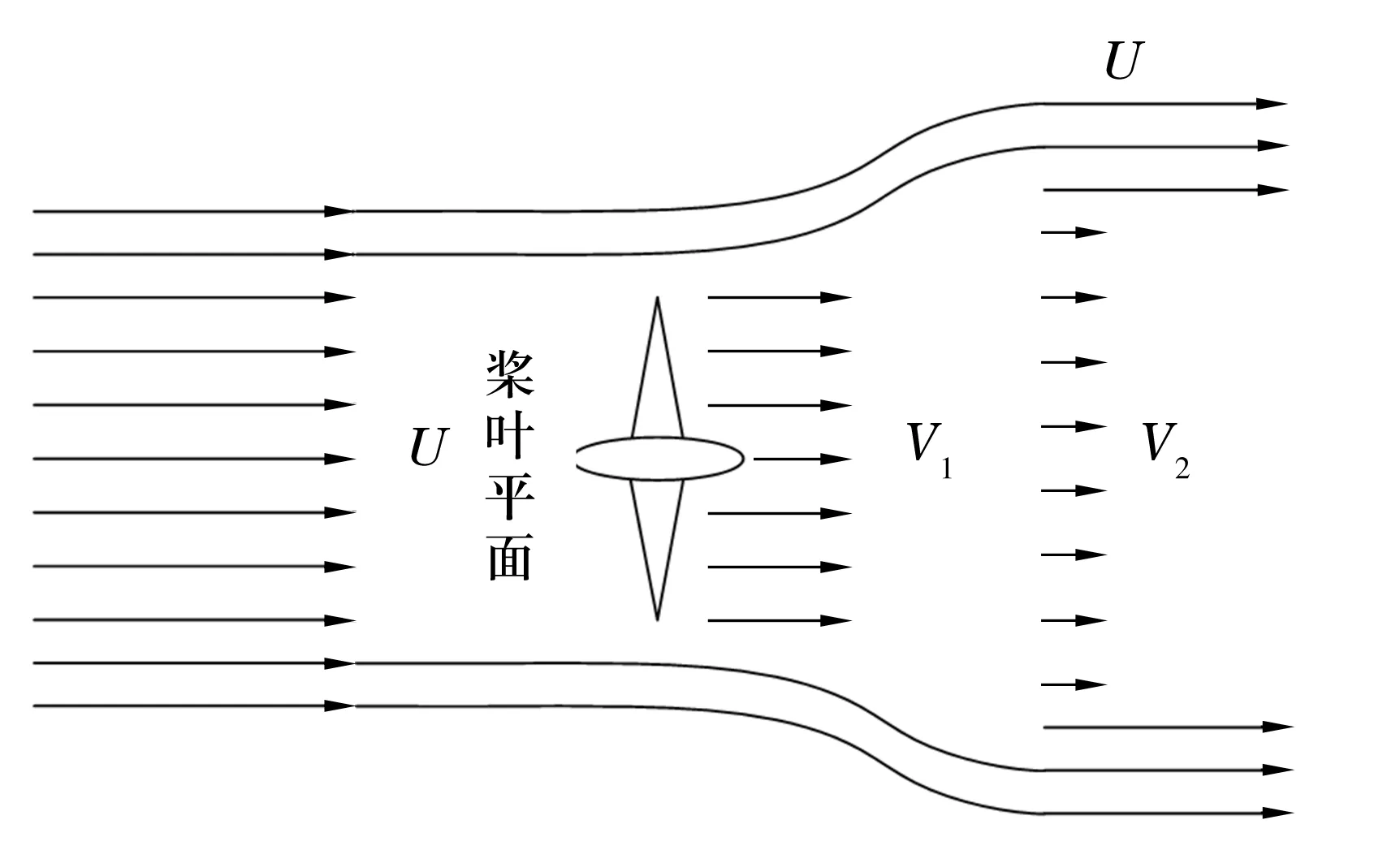
图4 风轮流场
(14)
式中:A为桨叶平面的面积;n为叶片数。
设叶片合力在y方向作用在Ly处,则
Fyb=Mxb/Ly,
式中:Ly可通过叶素理论精确求解得到,一般约为1/2叶片长度,本文简化计算取1/2叶片长度。

根据动量理论,作用于每根叶片的x向的推力为
Fxb=ρAU(U-V2)/3。
设叶片合力在x方向作用在Lx处,则
Myb=FxbLx,
式中:Lx可通过叶素理论精确求解得到,一般约为1/2叶片长度,在本文简化计算取1/2叶片长度。
设叶片重心在叶片长Lg(利用Pro/E对叶片进行实体建模得到)处,则叶片转动离心力为
Fg=mω2Lg。
3 实例计算
本文算例来源于国内某型号风机实际运行工况,叶片翼型为NACA634[9],具体参数见表1和表2。
3.1 桨叶离心力产生的变桨阻力矩Tc
玻璃钢桨叶密度ρb=1 700 kg/m3;风轮的计算角速度ω=πn′/30=πn/10=6.05 rad/s。每段桨叶长度dr可由表2中LB计算得到,即drn=LB(n+1)-LBn;叶片截面厚度c由表2中dc计算得到,cn=(dcn+dcn+1)/2。由(5)式得Tc=504 N·m。
3.2 运动副摩擦阻力矩
其主要指变桨回转支承摩擦阻力矩。

表1 风轮及风况参数

表2 桨叶截面参数
假设U=12 m/s,此时风机的风能利用率ηs约为40%,叶片重心和所受空气动力的合力均约在叶片中部,则
式中:Dlg,Lblade分别为轮毂直径和叶片长度。叶片长度Lblade由表2中LB估算得到,得Lblade=29.1 m。
Ly=14.55 m,Lx=14.55 m,Lg=14.26 m,Dpw=1.9 m,μ=0.006。将上述参数代入各式,最终由(10)式得Tf=25.6 kN·m。
3.3 空气动力产生的变桨阻力矩
假设叶片变桨纵轴在距前缘40%弦长处,合力F作用在弦长中点(50%弦长)处对变桨纵轴产生扭矩,则有Xf=50%b;Xd=40%b,结合表1和表2中的参数由(9)式得Ta=9.3 kN·m。
3.4 桨叶重心偏离桨叶变距轴而产生的重力矩
设桨叶轴均通过各截面重心,并位于风轮旋转平面内,即Tg=0。
3.5 总功率
T=Tc+Ta+Tg+Tf=35.4 kN·m。根据文献[10]对风力发电机的设计准则取a=1.25,ηc=0.95,当时工况下变桨速度为0.157 rad/s,则P=7.31 kW。
4 结束语
在以往的文献中计算离心力和空气动力引起的变桨距载荷都是运用叶素理论、动量理论等进行复杂的积分运算,计算时还需考虑诸多的计算参数。而文中的计算方法为适应工程上快速准确的解决问题需求,对前人的计算做了一定的简化,并且做了一些假设,系为一种保守的估算,而且还提供了计算变桨回转支承的摩擦阻力矩的计算方法,可为实际工程中相关驱动部件的选型提供参考。

