榆林地区设计洪水计算方法探讨

金孝华，冯光成，慕振莲

(黄河水利委员会绥德水土保持科学试验站，陕西绥德718000)

近年来，随着西部大开发战略的实施和淤地坝亮点工程的建设，作为多沙粗沙集中来源区和重化工基地，榆林地区防洪工程的建设速度和数量都在不断增加。在榆林地区水资源开发利用的水利规划和工程设计中，水文计算一直沿用《榆林地区实用水文手册》(以下简称《手册》)提供的方法，其中关于设计洪水的计算有4种方法，不同的方法得到的结果差异很大，给实际工程设计带来了困难。为验证《手册》中4种计算方法的精度和适用性，笔者以桥沟流域1994.08.04实测洪水和孤山川沙梁二道沟坝典型工程为例进行计算。

1 设计洪水计算方法

1.1 不同时段设计暴雨量计算

《陕西省中小流域设计暴雨洪水图集》(以下简称《图集》)和《手册》提供了年最大20 min、1 h、3 h、6 h、12 h、24 h 等不同时段的点雨量均值等值线图及相应时段点雨量变差系数等值线图。不同时段设计暴雨量计算公式为

式中:HP为不同频率不同时段设计暴雨量，mm;kP为不同频率对应的模比系数;H为不同时段年最大暴雨量均值，mm。

1.2 设计洪峰流量计算

《手册》中提供了4种设计洪峰流量的计算方法。

(1)汇水面积相关法，计算公式为

式中:QN为重现期为N的洪峰流量，m3/s;CN、n分别为重现期为N的地理参数和指数，可根据项目区位置在《手册》中洪峰流量—汇水面积相关参数表中查得;F为汇水面积，km2。

(2)综合参数法，计算公式为

式中:h6为重现期为N的设计流域6 h面雨量，mm;ξ为流域形状系数;α、β为经验指数;其余参数意义同上;CN、α、β、n可通过

查《手册》中的综合参数法经验公式分区参数、指数表获得。

(3)《手册》推理公式法(1/3推理公式法)，计算公式为

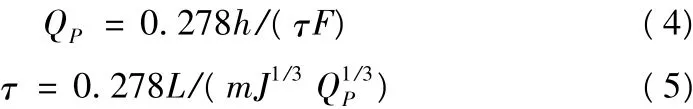
式中:QP为设计频率为P的最大洪峰流量，m3/s;τ为流域汇流历时，h;h为净雨深，mm，在全面汇流时为相应于τ时段的最大净雨，在部分汇流时为单一洪峰对应的面平均净雨;F为汇水面积，km2;L为沿主沟道从出口断面至分水岭的最长距离，km;m为汇流参数;J为沿程平均比降;0.278为单位换算系数。

其中净雨深(h)、汇流参数(m)、汇流历时(τ)的计算步骤依次为:①设计暴雨雨型，根据不同频率设计雨量进行雨型配置(或24 h内短历时暴雨分配)。②净雨推求，采用“入渗曲线法”扣损推流，其中前期影响雨量(Pa)、入渗率及土壤含水量关系曲线、产流过程及净雨过程等均可在《手册》中查算。③汇流计算，包括汇流参数(m)的查算、汇流历时(τ)及洪峰流量(QP)的推求等。在《手册》中查算出汇流参数(m)后，按式(5)假定QP计算并绘制Q—τ曲线，再根据净雨过程绘制Q—t曲线(t为洪水总历时)，两条曲线的交点对应的纵坐标即为所求的洪峰流量(QP)，横坐标即为汇流历时(τ)。

(4)水利行业标准推理公式法(1/4推理公式法)。水利行业标准《水土保持治沟骨干工程技术规范》(SL 289—2003)(以下简称《规范》)推理公式的计算公式为

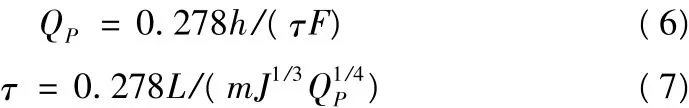
式中:参数意义同上;计算方法同1/3推理公式法。

1.3 设计洪水总量计算

设计洪水总量的推求主要有两种方法，前者适用于经验公式法，后者适用于推理公式法。根据《规范》，不同频率洪水总量的计算公式为式中:WP为频率为P的设计洪水总量，万m;a为径流系数;hP为频率为P的不同时段暴雨径流深，mm;其余符号意义同上。

1.4 设计洪水过程线推算

根据《规范》，采用概化三角形法推算设计洪水过程线，洪水总历时计算公式为

式中:T为洪水总历时，h;t1为涨水历时，h;t2为退水历时，h;WP为设计洪水总量，万m3;5.56为单位换算系数;其余符号意义同上。

概化三角形法中三角形顶点位置由涨水历时和洪水总历时的比值at1控制，at1=t1/T，其数值介于0.1～0.5 之间。用推理公式计算时，由于工程控制面积较小，涨水历时t1≈τ。

2 实测洪水分析

2.1 桥沟小流域1994.08.04实测洪水概况

桥沟小流域位于陕西省绥德县辛店乡，是裴家峁沟下游的一级支沟，流域面积0.45 km2，汇流比降0.117，主沟长1.4 km，平均宽 0.32 km，流域不对称系数 0.23，沟壑密度 5.4 km/km2，流域内有两条较大的支沟，均呈长条形。根据小流域1986—2008年降雨资料，采用《图集》中的经验公式验证降雨频率，经P－III频率适线分析，该流域多年平均最大24 h降雨量为57 mm，变差系数(CV)为 0.64，偏态系数Cs=3.5CV，由《手册》查得20年一遇模比系数(KP)为2.28，30年一遇模比系数(KP)为2.49，20年一遇的24 h降雨量为130.0 mm，30年一遇的24 h降雨量为141.7 mm。1994年8月4日桥沟小流域发生暴雨。经计算，该次暴雨实测降雨量为140.9 mm，与计算结果141.7 mm相近，因此桥沟流域1994.08.04降雨频率为3.33%，重现期为30年。

2.2 计算结果对比

以24 h为设计时段，采用不同计算方法推求相应频率设计洪水与实测暴雨洪水特征值及过程线，计算结果见表1。根据计算结果点绘实测与设计降雨、洪峰流量、洪水总量、洪水过程线(图1)。由图1知，1/3推理公式法计算所得的洪峰流量、洪水总量与实测值最为接近;1/4推理公式法计算的洪峰流量偏小;面积相关法和综合系数法计算的洪峰流量明显偏大，洪水总量则偏小。

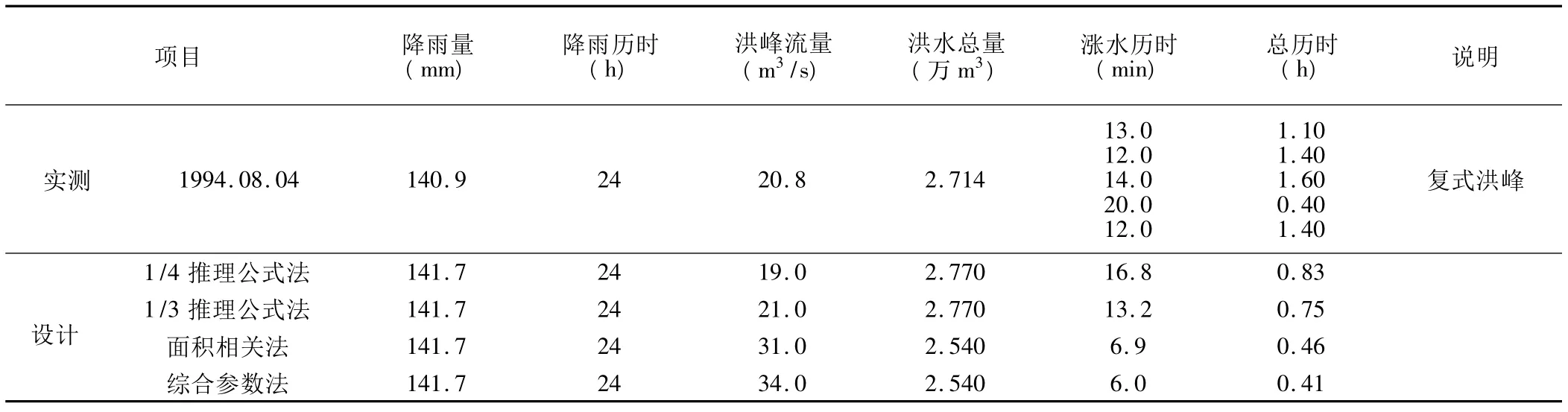
表1 桥沟小流域实测与设计降雨量、洪峰流量、洪水总量、洪水过程线对比

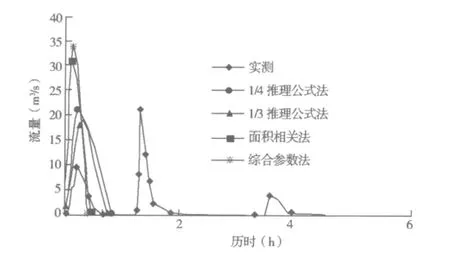
图1 实测暴雨洪水与设计洪水过程线比较

3 典型工程分析

为了进一步验证不同计算方法在实际工程设计中的精度，我们以孤山川沙梁二道沟坝为例，对不同计算方法的结果进行比较分析。孤山川沙梁二道沟坝位于黄土丘陵沟壑区，属沙梁川上游小流域，坝控面积2.1 km2，沟道长度4.27 km，沟道比降4.49‰。采用上述4种方法计算孤山川沙梁二道沟坝不同重现期的设计洪峰流量模数(表2)、洪水总量模数(表3)以及洪水过程线(表4)，可以看出:①洪峰流量模数。4种方法的计算结果差异较大，主要表现为经验公式法的计算结果一般较推理公式法大，其中综合参数法结果明显偏大，1/3推理公式法较1/4推理公式法结果偏大。②洪水总量。4种方法的计算结果比较接近。③设计洪水过程线。相比推理公式法，经验公式法计算得到的洪峰流量与洪水总量都不同程度地存在不协调的情况，洪水过程线差异较大。

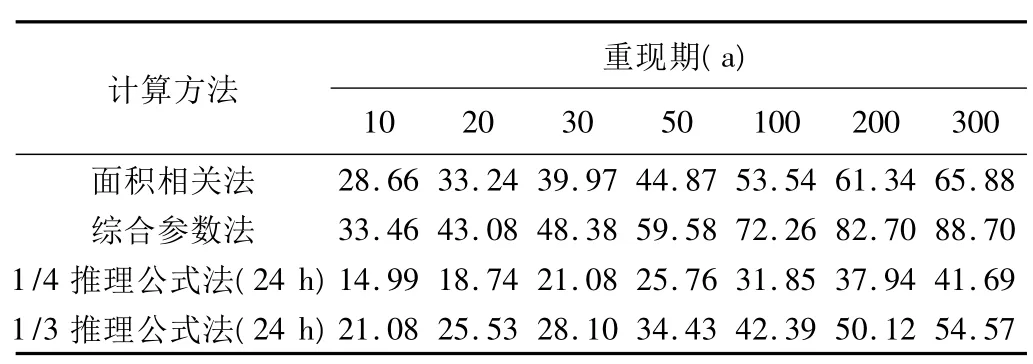
表2 不同计算方法的设计洪峰流量模数 m3/(km2·s)

表3 不同计算方法的洪水总量模数 万m3/km2

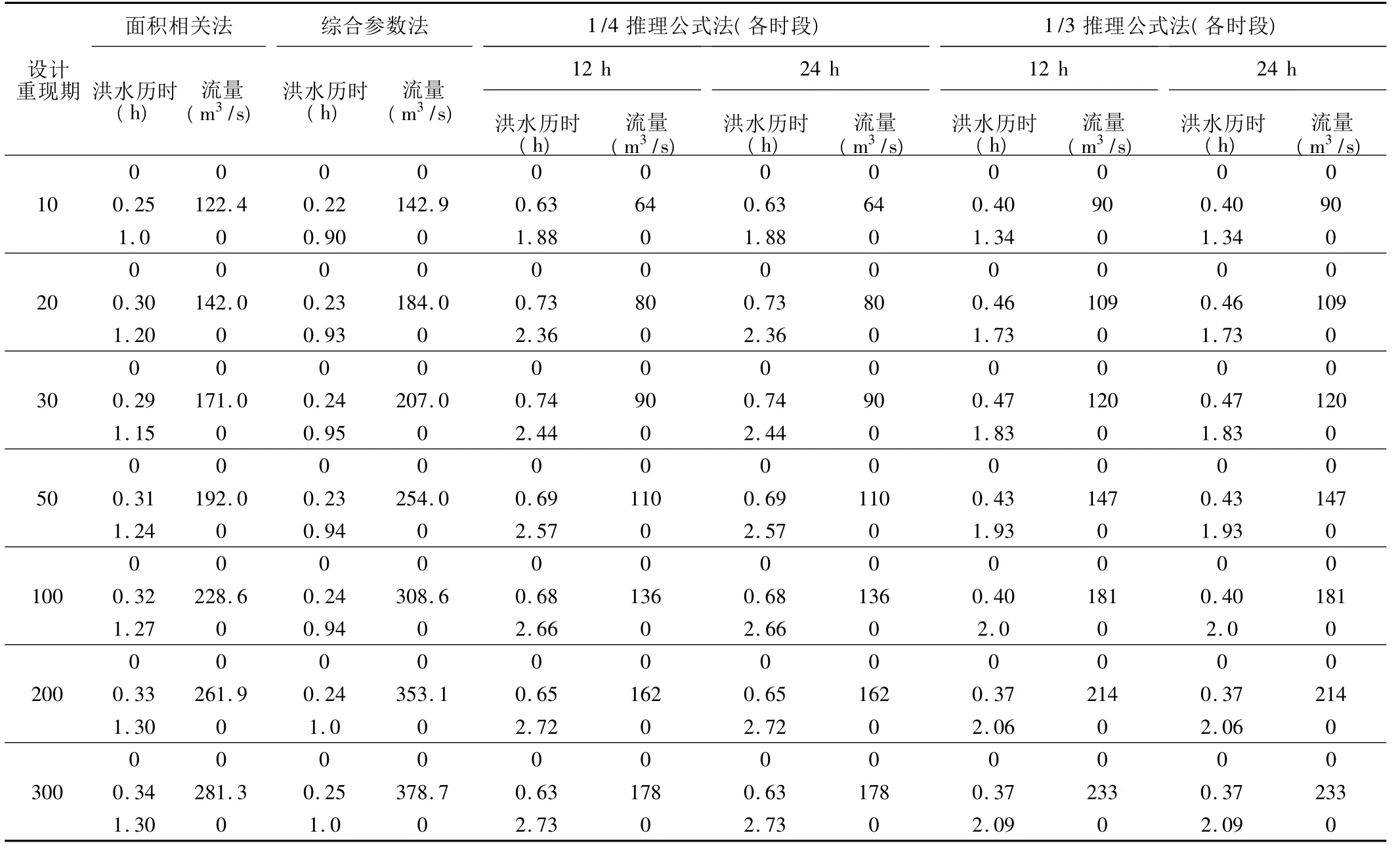
表4 不同计算方法的设计洪水过程线

4 结果分析

图1是采用小时段(20 min)拟合的降雨过程线，从图1中实测暴雨洪水与相应频率设计洪水过程线的对比结果可以看出，采用1/3推理公式法计算得到的不同暴雨时段设计与实测洪水特征值比较相符，拟合精度在86%以上，尤其是采用最大24 h暴雨时段设计洪水的拟合效果最为理想，洪峰流量、洪水总量、涨水历时的拟合精度分别为99%、98%和91%，说明1/3推理公式法的计算结果与实际情况基本吻合。

综合上述计算结果和分析论证，笔者认为在榆林地区进行水资源开发利用的水利规划和工程设计过程中的洪水水文计算时，采用1/3推理公式法进行设计洪峰流量、设计洪水总量和设计洪水过程线计算较为合理。