考虑混凝土损伤的双面组合连续梁挠度和裂缝宽度研究
张 岩, 段树金, 郑 岗
(石家庄铁道大学土木工程学院,河北石家庄050043)
0 引言
钢-混凝土组合连续梁内支座负弯矩区的混凝土板在荷载作用下受拉很容易开裂,开裂后由板内钢筋的屈服和钢梁的屈曲决定该结构的承载力,组合梁刚度降低。通过裂缝渗入到混凝土内的污水或有害气体使结构的耐久性降低,维修养护困难[1]。因此,为保证结构的正常使用,应对钢-混凝土组合连续梁的裂缝问题进行系统深入地研究。
组合梁的开裂实际上是翼缘板-钢筋混凝土构件受力逐渐损伤,直至开裂失效的过程。也就是说混凝土的开裂是有过程的,裂面的正应力随着混凝土拉应变或裂缝的增加而逐步减小,并非立刻降低到零,这一应力应变发展过程可以通过混凝土的拉伸软化曲线加以定义[2]。这与传统破坏理论只注重变形至破坏的起点-终点的研究方式不同,引入损伤的研究方法可以使人们对材料的力学性质认识的更深刻。
文献[3]~文献[6]进行了2跨双面组合连续梁的模型试验,建立了相应的空间有限元分析模型,系统研究了双面组合梁的受力性能和破坏特征,得到了梁的荷载-挠度曲线。在这些工作的基础上,针对负弯矩区翼缘板混凝土受拉裂缝进行研究,考虑混凝土拉应变软化特性,建立双面组合试验梁的平面有限元分析模型;分别讨论下混凝土板厚度和混凝土极限拉应变值对双面组合梁挠度和裂缝宽度的影响;采用最小二乘法,对荷载-挠度,荷载-最大裂缝宽度曲线进行拟合,得出相应的计算公式,为双面组合连续梁这一新型结构的设计和应用提供参考依据。
1 试件参数
试件如图1。所用材料:混凝土采用C30,配合比为1 m3混凝土需W:190 kg,C:380 kg,S:726 kg,G:1 090 kg;测得混凝土试块28 d强度平均值为47 MPa;轴心抗压强度37.6 MPa,弹性模量平均值为46.2 GPa;钢梁采用H型钢HW150×150×7×10,截面面积为40.55 cm2,单位长度质量为31.9 kg/m,Ix-x=1 660 cm4;加劲肋采用10 mm厚热轧Q235钢板,尺寸为130 mm×72 mm×58 mm,加劲肋和钢梁间采用双面角焊缝;剪力连接件采用Φ13×60的圆柱头栓钉[3,5]。
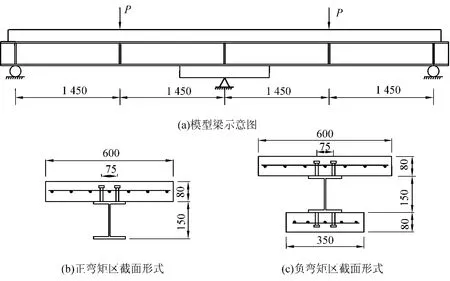
图1 模型梁及截面尺寸图(单位:mm)
2 平面有限元模型的建立
2.1 单元的选择
混凝土、钢梁均采用Plane82单元,上翼缘板内钢筋选用Link1单元;钢筋与混凝土之间的粘结滑移和栓钉均由Combine39非线性弹簧单元模拟。
2.2 混凝土的本构关系和破坏准则
(1)单轴受压混凝土。单轴受压混凝土的本构关系采用《混凝土结构设计规范》(GB50010—2002)附录C建议的应力-应变关系。根据试验及相关内容,确定应力-应变曲线上的点,在ANSYS中,通过多线性等向强化模型(MISO)实现,该本构关系中的相关参数取值如下:εc=1 756.4×10-6;εcu=3 597.1×10-6;fck=37.60 MPa;εt0=6×10-5;εtu=3×10-4;ftk=2.59 MPa。
(2)单轴受拉混凝土。为简化分析过程,单轴受拉混凝土采用考虑下降段的双直线模型。在ANSYS中,多线性随动强化模型(MKIN)合理的选取参数后可以描述下降段,反映混凝土的“软化”[2],混凝土的破坏准则采用最大拉应变准则。相关参数取值与(1)中相同。
2.3 钢材的本构关系
钢梁、混凝土板中的钢筋均采用理想弹塑性模型,分析中屈服准则使用双线性随动强化模型(BKIN)。其中,钢材屈服强度fy=235 MPa,泊松比为v=0.3;假定其受压与受拉时弹性模量相同,钢梁和钢筋的弹性模量Es分别为206 GPa、210 GPa。
2.4 网格划分及荷载的施加
网格划分时,按照映射方式进行,混凝土和钢梁单元均划分为四边形单元;结合研究重点,混凝土板单元尺寸相对于其他构件要小,经反复调试,确定为10 mm;考虑到钢筋混凝土之间双弹簧单元间距对收敛性的影响,钢筋单元尺寸按照双弹簧单元间距50 mm来设置。
加载位置与试验相同,为了处理混凝土软化问题,采用位移加载方式;为加快收敛,非线性计算采用修正的Newton-Raphson方法求解。试验梁有限元模型如图2所示。
2.5 裂缝的处理
混凝土中裂缝的形成与发展过程可认为是损伤不断积累、程度不断增加的过程,这一过程可以用混凝土弹性模量降低的过程来表示[7]。

图2 试验梁模型及网格划分图
分析过程中,采用混凝土四边形单元4个节点拉应变的平均值ε来控制,如图3所示,即当混凝土单元的平均拉应变εt达到受拉混凝土的峰值应变εt0时,混凝土开裂,继续加载,应变增加而应力、弹性模量逐渐减小,待混凝土单元的平均拉应变εt达到受拉混凝土的极限拉应变εtu后,利用ANSYS的“单元生死”功能将该单元杀死,即赋予该单元一个很小的刚度值,认为此单元已完全不能承担拉应力,从而模拟混凝土的断裂。如此循环,裂缝逐渐扩展;最后,通过上混凝土板顶面开裂单元相邻边缘节点的相对位移计算裂缝宽度。
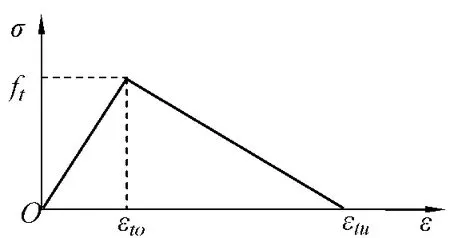
图3 受拉混凝土σ-ε关系
3 有限元计算结果与实测结果的对比
通过有限元计算得到荷载-挠度、荷载-最大裂缝宽度曲线,其与试验结果的比较如图4和图5。ANSYS计算结果与试验结果吻合较好,可见所选取的有限元模型是合理的。
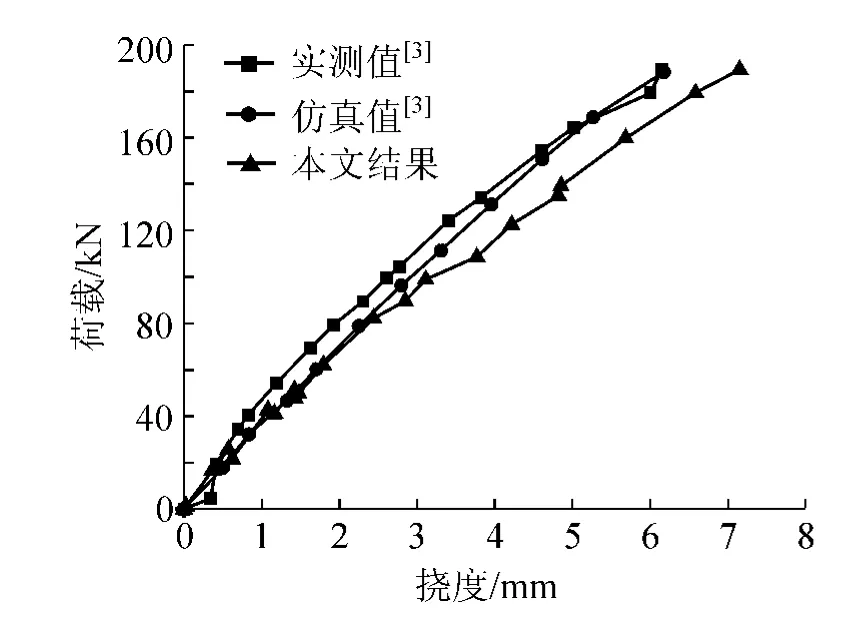
图4 试验梁荷载-挠度曲线

图5 试验梁荷载-最大裂缝宽度曲线
4 截面材料参数对梁挠度和最大裂缝宽度的影响
在上述模型的基础上,改变下混凝土板厚度和混凝土极限拉应变等参数,相应的组合连续梁的挠度和最大裂缝宽度的变化情况见图6~图9。
5 结果分析与对比
采用最小二乘法,利用数学软件Matlab进行曲线拟合,确定挠度和最大裂缝宽度的计算公式。
不同下混凝土板厚度下挠度和裂缝计算结果见表1。参数分析的计算结果表明:厚度越小,刚度越小,开裂荷载越小;加载初期,裂缝宽度相差不大,随着荷载增加,裂缝发展速度加快;相比普通组合梁,双面组合梁的弹性极限荷载提高了50%,证明下混凝土板厚度对最大裂缝宽度的影响,因此,适当加大下混凝土板的厚度是必要的。

图6 不同下混凝土板厚度下梁的挠度
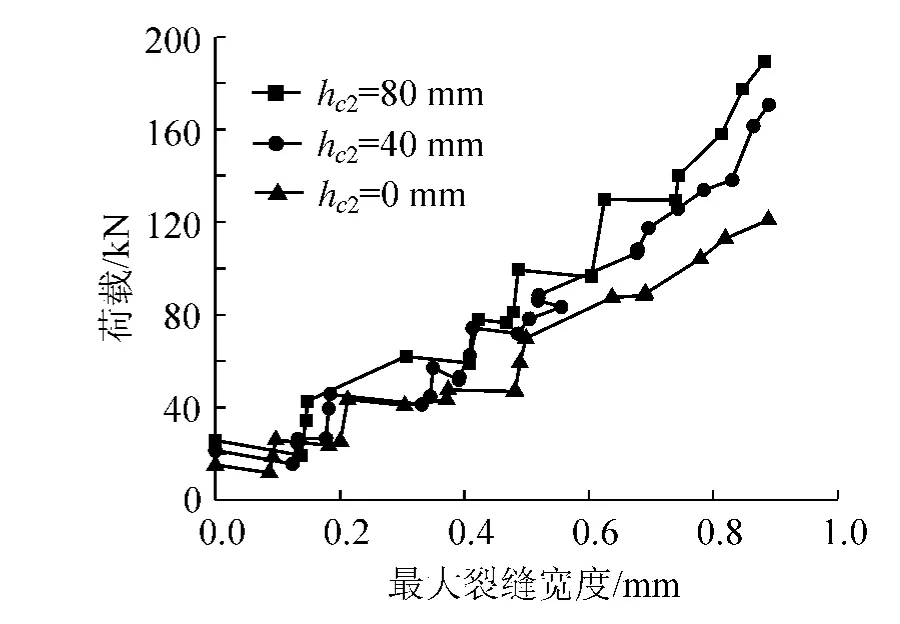
图7 不同下混凝土板厚度下梁的最大裂缝宽度

图8 不同混凝土极限拉应变下梁的挠度

图9 不同混凝土极限拉应变下梁的最大裂缝宽度

表1 不同下混凝土板厚度下的计算结果对比
f-hc2计算公式:-0.008 022hc2+2.36。w-hc2计算公式:w=-0.001 231hc2+0.144 9。
不同混凝土极限拉应变下的计算结果见表2,参数分析结果表明:双面组合连续梁的开裂荷载、刚度随混凝土极限拉应变的提高而增加,最大裂缝宽度随混凝土极限拉应变的提高而减小,证明混凝土极限拉应变的提高,在一定程度上可以推迟混凝土的开裂,减小裂缝宽度,使结构刚度增加。

表2 不同混凝土极限拉应变下的计算结果对比
6 结论
(1)采用有限元法评价双面组合连续梁的裂缝宽度是可行的。
(2)加载过程中,双面组合连续梁负弯矩区翼缘板有3条主裂缝出现,其裂缝分布与试验结果基本一致。
(3)适当加大下混凝土板厚度可以有效推迟混凝土的开裂,减小双面组合梁混凝土翼缘板的裂缝宽度。
(4)受拉混凝土板的开裂是一个渐进的过程。使用高性能混凝土,增加了受拉混凝土的极限拉应变,可以有效延迟混凝土板的开裂,减小裂缝宽度。
[1]HYO GYOUNG KWAK,YOUNG JAE SEO.Long-term behavior of composite girder briges[J].Computers and Structures,2000,74:583-599.
[2]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.
[3]段树金,周庆东,王海良,等.钢-混凝土双面组合连续梁的承载能力试验研究[J].铁道科学与工程学报,2008,5(5):12-17.
[4]段树金,霍军会,安蕊梅.钢-混凝土双面组合连续梁承载能力研究[J].铁道学报,2010,32(5):82-87.
[5]周庆东.钢-混凝土双面组合连续梁模型试验研究[D].石家庄:石家庄铁道学院土木工程分院,2007.
[6]霍军会.钢-混凝土双面组合连续梁正截面强度计算方法研究[D].石家庄:石家庄铁道学院土木工程分院,2007.
[7]钱觉时,吴科如.砼损伤带裂缝模型[J].重庆建筑工程学院学报,1993,15(3):9-18.

