统一潮流控制器(UPFC)在电压稳定性中的应用
李明礼,付康
(1.广西大学电气工程学院,广西 南宁 530004;2.安微省阜阳市供电公司,安徽 阜阳236000)
1 引言
电压稳定性一直都是电力系统规划和运行的重要研究对象。20世纪80年代以来,世界范围内发生了多起严重的由系统电压失稳导致整个系统崩溃的事件,使人们更加认识到电压稳定的重要性[1]。
随着电力电子技术、信息技术和控制理论的飞速发展及综合应用,出现了很多控制电压稳定的设备。其中FACTS以其特有的大功率、高速、精确连续的控制特点在提高系统的稳定性和可靠性方面得到越来越多的应用。UPFC综合了FACTS元件的多种灵活控制功能,可以控制系统电压,还能对线路的有功和无功潮流进行控制,从而达到优化系统的作用。
灵敏度分析方法利用系统中某些量的变化关系来分析其是否稳定,因其计算简单,在电压稳定研究中得到越来越广泛的应用。本文使用dUL/dPL作为灵敏度指标[2],分析UPFC装设后给系统带来的诸如节点电压、灵敏度指标等方面的影响。
2 UPFC的工作原理
如图1所示:统一潮流控制器的主电路由两个电压源型逆变器组成,并通过两个变压器接入系统[3]。逆变器1通过变压器T1并联接入系统(简称并联部分),其主要作用是提供或吸收由逆变器2在公共的直流母线上的有功功率,以维持UPFC的有功功率平衡,也可产生和吸收无功功率,维持送端节点电压稳定;逆变器2通过变压器T2串联接入系统(简称串联部分),其作用是向系统注入一个与输电线路同频率的可调的交流电压Upq,使UPFC能对输电线路的电压、阻抗角、有功和无功功率等进行单独或者综合控制。逆变器1与逆变器2通过中间的直流电容C连接,含UPFC的传输系统的向量图如图2所示。

图1 UPFC的简化模型示意图

图2 含有UPFC系统的向量图
3 UPFC 的数学模型[4]
装设有UPFC装置的线路的等效网络如图3所示。
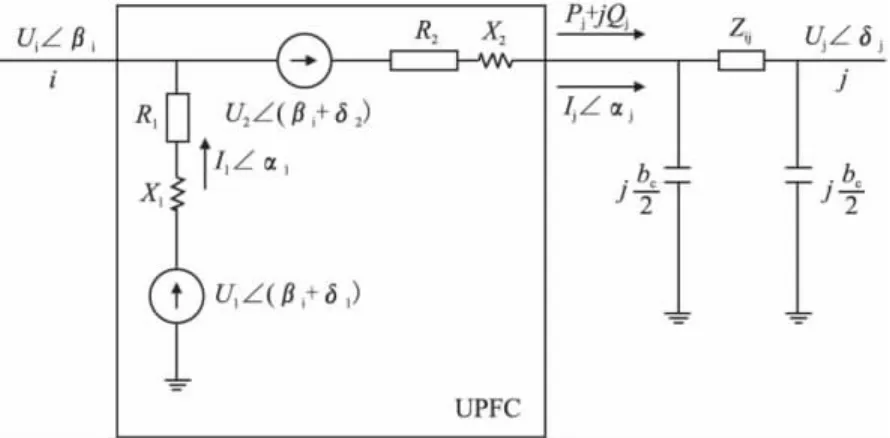
图3 UPFC的数学模型
逆变器1的输出电压为U1,超前送端节点电压Ui的相位为δ1;逆变器2的输出电压为U2,超前Ui的相位为δ2;X1、X2分别为并联变压器T1和串联变压器T2的漏抗;R1为包括逆变器1损耗和T1损耗在内的等效电阻,R2为包括逆变器2损耗和T2损耗在内的等效电阻。
由功率平衡关系得到直流侧电容C两端电压Ud的变化方程,即电容C储能的变化率等于UPFC吸收的总的瞬时有功功率,应有:
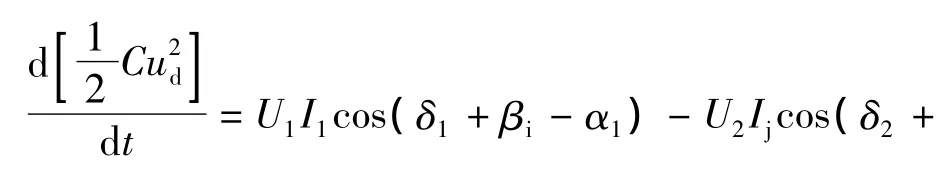

动态时UPFC两侧的有功平衡,有:

并联端电流I1的表达式为:

UPFC 逆变器采用 S- PWM 技术控制[7]U1、U2作为直流侧电容电压ud的输出:

其中:k1,k2分别为并联和串联换流器的调制比,其值为各自的调制波UP和载波UT的波峰值的比值;δ1和δ2为调制波节点i电压波形的相位差。
4 含UPFC电网的U-P灵敏度指标

U-P灵敏度指标的数学模型[5]:


在常规静态电压稳定性分析中,通常可以假设发电机与负荷节点有功功率偏差量ΔP=0,即有:
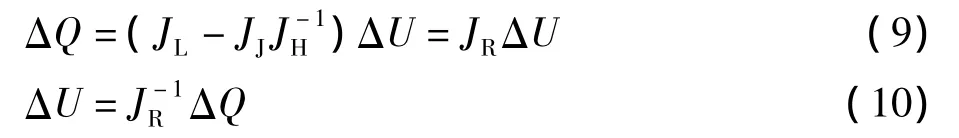
式中:为节点i的U-P灵敏度值。
现以图4为例利用注入功率法[3]推导计及UPFC的U-P灵敏度指标值:

图4
UPFC的附加注入功率为:
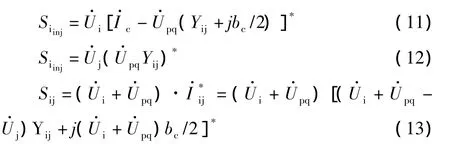
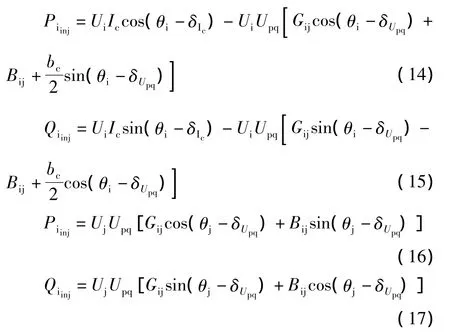
节点i,j的功率不平衡方程为:


UPFC支路自身的有功功率平衡方程:

将式(21)代入方程组(18)和(19)再结合目标约束方程式(20)得到只增加了两行两列的新的装设有UPFC的雅可比矩阵:

对此新的雅可比做如前计算,就得到计及UPFC的节点U-P灵敏度指标。
5 算例分析
本文采用仿真工具PSAT1.3.4对WSCC-3机9节点系统(如图5)进行仿真,1为平衡节点,2、3为PV节点,5、6、8为负荷节点。除了电源节点外,其它节点都缺乏无功支持,特别是三个负荷节点应为系统的不稳定节点。

图5 WSCC-3机9节点系统图
初始运行状态下,系统各节点电压及U-P指标的仿真计算结果如表1所示。

表1 WSCC9系统各节点灵敏度指标值
所有负荷节点功率按5%逐次增加直至系统电压出现崩溃(即使Jacobian矩阵出现奇异的点)时,各节点的U-P指标值如表2所示。

表2 负荷按5%增加至电压崩溃临界点时节点的灵敏度值
以上数据表格反映5、6、8三个节点在初始状态下电压相对偏低,且U-P灵敏度指标值在初始状态和负荷激增时都相对偏大,下面在节点6安装UPFC,则节点6的电压和灵敏度指标值如下表。安装的UPFC参数如下:容量SN=100MVA,电压UN=230kV,频率fN=50Hz;并联接入点参考电压Uref=1.05p.u.;直流侧参考电压 Udref=1.02p.u.。
不考虑负荷量的变化时,节点6的电压和灵敏度值如表3所示。
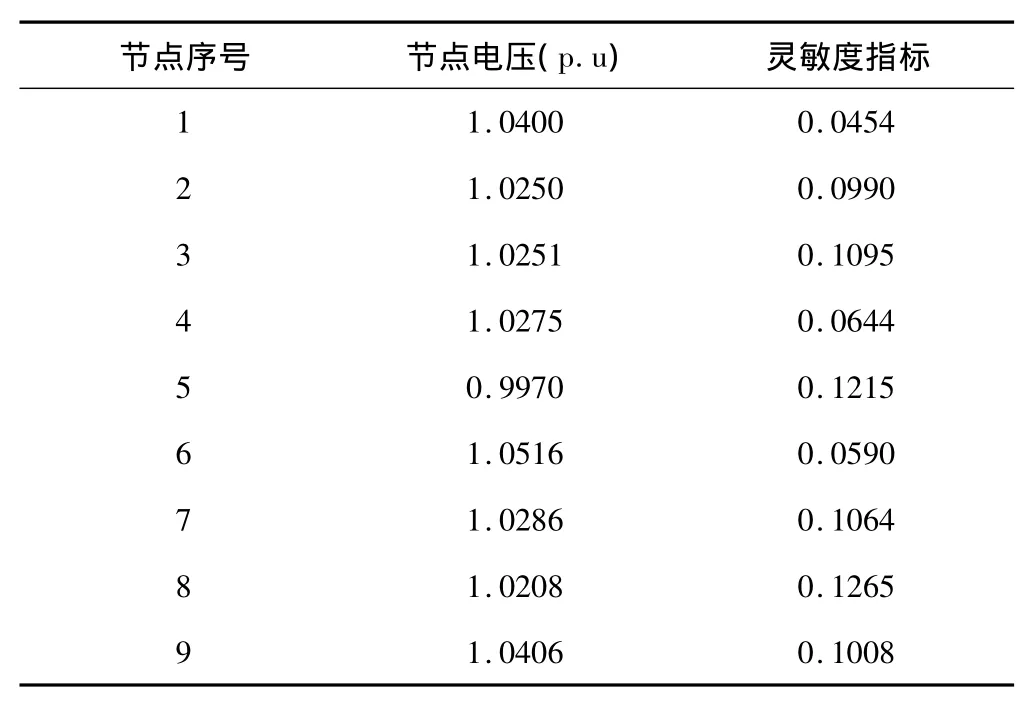
表3 节点6安装UPFC后各节点的灵敏度指标值
所有负荷节点功率按5%逐次增加直至系统电压出现崩溃(即使Jacobian矩阵出现奇异的点)时,各节点的U-P指标值如表4所示。
通过以上数据不难看出,系统除了平衡节点和电源节点外,安装UPFC后节点电压都有所提高,节点的灵敏度也在一定程度上有所改善;当节点量增加时,仿真得到的各节点的灵敏度与初始系统相比在装设UPFC后节点指标也都有所改善,特别是在节点安装处指标值改善最为明显。

表4 装设UPFC后节点5按5%增加至电压崩溃临界点时节点的灵敏度值
6 结论
本文通过仿真,从理论上说明,系统装设UPFC后能使电压低的节点得到改善,对线路的潮流能有效的控制,提高了系统的电压稳定性,优化系统运行,为电力的研究提供了一种有效的控制方法,拓宽了思路。但本文只对比分析了在简单系统下安装UPFC时节点6的仿真结果,如在复杂系统情况下对所有电压偏低节点安装UPFC后是否能改善系统的电压稳定性能还有待进一步的研究。
[1]傅旭,王锡凡,杜正春.电力系统电压稳定性研究现状及其展望[J].电力自动化设备,2005,25(2):1 - 9.
[2]段献忠,袁骏,何仰赞,等.电力系统电压稳定灵敏度分析方法[J].电力系统自动化,1997,21(4):9 -1.
[3]徐琰,李乃湖,王海风,等.基于统一潮流控制器(UPFC)的电力系统稳态潮流控制的模型和算法[J].电力系统及其自动化学报,1996,8(3):1-6.
[4]李庚银,徐春侠,律方成,等.含FACTS元件的电力系统潮流计算[J].华北电力学院学报,1996,2(23):4 -5.
[5]Fuerte - Esquivel C R,Acha E.Unified power flow controller:acritical comparison of Newton -Raphson UPFC algorithms in power flow studies.IEEE proc.September,1997,144(5).
[6]龙军,胡慧艳,庞敏,等.带SVC电力系统电压稳定二阶指标的计算与仿真[J].广西大学学报(自然科学版),2008,33(2):196 -200.
[7]Iwamoto S,Tmaura Y.A Load Flow Calculation Method for IEEE Trans on Power Systems,1991,100(4):1736 -1743.
[8]袁俊,段献忠,何仰赞.电力系统电压稳定灵敏度分析方法综述[J].电网技术,1997,21(9):7 -10.
[9]葛敏辉,石松气,周贵兴.UPFC控制器设计原理及方案[J].电网技术,2000,6,24(6):31 -33.

