智能蚂蚁算法在电力系统无功优化中的应用
刘欣,王晋
(1.长治供电分公司,山西 长治 046000;2.山西晋城供电分公司,山西 晋城 048000)
1 序言
随着国民经济的快速发展,电力系统网架结构和运行方式日益复杂,这就对系统运行的可靠性要求越来越高。电压是电力系统运行安全性和经济性的重要指标,它直接反映了系统的无功平衡状况。而衡量一个系统的电压水平好坏的两个主要的因素一个是电压的幅值是否在合理的范围内,其次是电压波动的幅度。系统的运行电压太低会导致损耗增加,严重时甚至可能引起电压崩溃,而电压太高超过了设备的耐受极限,同样会引起设备的绝缘破环,从而影响系统的安全稳定运行。
无功优化的方法很多,总的来说可以分为两类:一类是常规优化方法,它们从某个初始点出发,按照一定的轨迹不断改进当前解,最终收敛于最优解。这类优化方法有线性规划法、二次规划方法、非线性规划法及混合整数规划法等[1]。另一类是所谓的智能优化算法,它们从一个初始解群体开始,按照概率转移原则,采用某种方式自适应地搜索最优解。主要包括遗传算法、模拟退火算法、禁忌搜索(Tabu Search)以及各种进化规划方法。都能用来解决电力系统的无功优化问题,但要求优化问题可微,对离散变量的处理缺乏指导性,而目通常只能求得局部最优解[2]。本文在蚁群算法的基础上,提出了一种新的启发式搜索算法—智能蚂蚁系统,智能蚂蚁系统通过对蚁群算法的改进,在减少计算量的同时,通过遗传操作处理离散变量,以较大的概率求得全局最优解。同时能为实际工程问题提供一系列的最优、次优解,以便选择,避免维数灾难,满足实际需要。将其应用于电力系统的经济调度和系统的无功优化,取得了令人满意的搜索结果。
2 蚂蚁算法
蚂蚁算法(ant algorithm,AA)是近年来刚刚诞生的随机优化方法,它是一种大自然的新的仿生类算法,由意大利学者M.Dorigo等最早提出的,该算法模仿蚂蚁觅食时的行为,按照启发式思想,通过信息传媒—外激素(Pheromone)的诱发作用,即通过蚂蚁群体之间的信息传递而达到寻优的目的,最初又称群蚁优化方法,由于模拟仿真中使用了人工蚂蚁的概念,因此亦称蚂蚁系统。其原理是通过一种正反馈机制或增强型学习系统,它通过信息素的不断更新达到最终收敛与最优路径上,逐渐收敛到问题的全局最优解,蚂蚁算法自问世以来表现出了强大的生命力,较之以往的启发式不论在搜索效率上,还是在算法的时间复杂度方面都取得了令人满意的效果,该算法己被其他领域的专家所接受,并运用到诸如分类、任务分配、机器人合作规划、图着色、车辆调度、大规模集成电路设计、通信网络中的负载平衡等许多方面[1]。但人工蚂蚁决不是对蚂蚁的一种简单模拟,它融进了人工智能,不仅适合目前的串行计算机,而且也适合未来的并行计算机,它不仅是一种全局优化方法,而且是一种正反馈机制,但初期信息素匾乏,求解速度慢。
3 蚁群算法
3.1 蚁群算法
蚂蚁算法具有并行性、正反馈、健壮性等特点,且搜索过程不需要人工干预,在解决小规模(n<30)的旅行商问题时效果显著但对于规模较大的问题,其性能会迅速恶化,其主要原因是,算法的初始阶段,各条道路上的外激素水平基本相等,蚂蚁的搜索呈现出较大的盲目性,只有经过较长时间后,外激素水平才呈现出明显的指导作用[3]。另外,由于蚂蚁算法是一种正反馈算法,在算法速度收敛较快的同时,也容易陷入局部优化,对蚂蚁算法的上述不足,导致其在处理大规模旅行商问题时性能下降明显,1996年,(Marco Dorigo)提出了蚁群算法,蚁群算法的改进主要有三点:
(1)蚂蚁选择目标城市的方法;
(2)外激素的全局更新;
(3)外激素的局部更新。
3.2 蚁群算法分析
除了蚁群算法外,还有另一类改进算法—最值蚂蚁算法这两种算法的主要思想是一致的,即一方而加强正反馈的效果,提高蚂蚁的搜索效率;另一方面,采用一定措施,减小陷入局部优化的可能性,虽然在所有蚁群算法的文章中都把外激素的局部更新作为其算法的特征之一,但通过实验发现,其作用是有限的,由于外激素的全局更新作用,在经过几次搜索以后,所有属于最佳路径的边,其外激素水平远远高于其它边(相差一个数量级)。因此,外激素的局部更新作用不能有效地阻止搜索陷入局部最优化另外,由于外激素的局部更新在每一步搜索之后都要进行,因此,消耗了大量的计算时间[4]。
蚁群算法的另一不足之处是:许多参数的设置凭借经验,没有充足的依据另外,蚂蚁数量的设定往往依赖于实验结果进行调整。因此,应用蚁群算法求解规模较大的不确定问题时,需先进行实验,根据结果调整参数,然后再进行搜索,但这不利于算法的广泛应用。
4 智能蚂蚁算法
通过对蚁群算法的改进,我们提出了智能蚂蚁算法,智能蚂蚁算法对蚁群算法的改进主要体现在以下四个方面:(l)取消外激素;(2)自动调整选择最优路径的比例;(3)改变了选择目标城市的依据;(4)引入扰动。
4.1 取消外激素
外激素是蚁群算法中蚂蚁实现通信的媒介,指导蚂蚁的前进方向。但是,由于蚂蚁的每一步运动都要更新外激素,要占用大量的CPU时间,通过对蚁群算法的考察可以发现,由于局部更新的作用,除最优路径外的所有边,其外激素水平相差无几,而最优路径与其他路的外激素水平则差异巨大,这在搜索的后期尤其明显。因此,如果取消外激素,即以q0的比例选择最优路径,1-q0的比例选择其他路径,可以大量减少计算,同时搜索的性能不会有太大的变化。实际上,在智能蚂蚁系统中,有两个比例参数qg和qi,分别代表选择全局最优路径和上次迭代搜索中最优路径的比例(qg+qi<1)通过引进qi,蚂蚁的搜索范围不局限于全局最优路径的周围,这样,可以避免重复搜索,也就达到了蚁群算法中局部更新的目的。
4.2 引入扰动
尽管采取多种措施,局部最优往往还是难以避免在智能蚂蚁系统中,通过扰动的引入使搜索跳出局部最优。我们对引入的扰动进行定义:无效搜索次数,当前的搜索次数与最近一次改进了结果的搜索次数的差值,定义为无效搜索次数在智能蚂蚁系统中,引入扰动的标准为:Iter_Inv=2·Iter_Lst+10000,式中Iter_Inv是无效的搜索次数,Iter_Lst是最近一次改进结果,引入扰动的方法是把qg和qi都减半,在所有蚂蚁都完成一次搜索后,选取其中结果最好的作为全局最优路径和结果,恢复qg和qi的值。
5 智能蚂蚁算法数学模型
由于最初的蚂蚁算法思想起源于离散型的网络路径问题,因此,若要用于一般的函数优化,必须对许多实施细节加以修正,我们先来考察最简单的一维搜索。
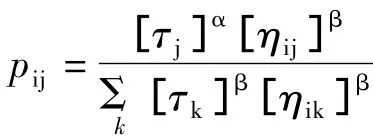
不难看出,一旦蚂蚁个数足够多,搜索半径足够小,这种寻优方式相当于一群蚂蚁对定义区间[a,b]做地毯式的搜索,逐渐收敛到问题的全局最优解。毫无疑问,上述的函数优化思想较之经典搜索方法,从一个孤立(往往是盲日)的初始点出发进行寻优的过程具有明显的优越性和稳定性,并且不受优化函数是否连续,是否可微等限制。
6 电力市场下的无功优化的数学模型
无功优化是指在满足系统运行约束的条件下,通过调整电网中的电压、无功分布(如调整发电机机端电压、无功补偿设备出力及可调变压器的分接头),使系统的有功网损最小。在不考虑无功成本时,传统无功优化的数学模型中,其目标函数一般只考虑节约网损的收益无功优化是一个多目标、非线性的函数优化问题,其数学模型如下:
6.1 目标函数
在电力市场条件下,电网购入的无功应该分成两部分,一部分是为保证电网电压合格无条件购入的无功,另一部分是为降低网损而购入的无功。因此,无功优化的目标函数也应该相应分成两个,一个是电压校正目标,其目的是在保证电压合格的前提下,使无功费用最少;一个是综合优化目标,其目的是在电压合格的前提下,使无功费用和网损综合最小,分别如下:
(1)电压校正目标函数

(2)综合优化目标函数

6.2 等式约束
(1)节点有功功率约束

(2)节点无功功率约集

6.3 变量约束
变量约束分控制变量约束和状态变量约束。
(1)控制变量的约束
①节点电压安全约束
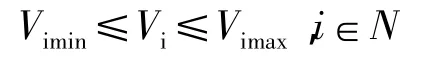
②发电机节点无功范围约束

③变压器分接头位置变化范围约束

(2)状态变量的约束为无功补偿节点无功装设容量的约束

上述各式中 ΔP(VG,QC,T)表示有功网损;ΔP0表示电压合格的初始网损;CP表示有功电价;CQGi(QGi)表示机组i的无功费用函数;CQGi(QGi)表示无功补偿装置i的无功费用函数;CQTi(Ti)表示变压器i的无功费用函数;SG表示机组集;SC表示无功补偿装置集;ST表示变压器集;N表示系统节点集;i表示系统中第i节点;n表示除平衡节点外的系统节点集;NT表示可调变压器的节点集;NC表示无功补偿节点集;NPV表示PV节点集;NVθ表示平衡节点号;PGi表示节点i有功出力;QGi表示节点i功出力;PDi表示节点i的有功负荷;QDi表示节点i的无功负荷;Vi节点i的电压幅值;θij表示节点i,j间在时段的相角差;Gij表示节点i,j间的导纳值;Bij表示节点i,j间的电纳值;QCi表示无功补偿节点i的容量;Ti表示变压器i的变比;Vimin,Vimax表示节点i的电压上下限;QCimin,QCimax表示无功源i的无功功率上下限;VDimin,VDimax表示无功源 i的电压上下限[5,6]。
6.4 控制变量
以发电机母线电压、有载变压器分接头的位置及无功补偿容量为控制变量。在建立无功优化数学模型时,我们作了如下假设:
(1)系统的有功分配已经完成,即认为在无功优化过程中,除平衡节点外,各节点的有功不变;
(2)系统电网结构确定;
(3)节点电压的改变对系统频率及负荷的影响可忽略,即认为在无功优化过程中,系统频率和负荷不发生变化[7]。
6.5 计算步骤
(1)对问题进行分析,根据上面的无功目标定义目标函数和等式约束函数;
(2)在第一个时间单位,每只蚂蚁从相邻节点集合随机地选择一个节点,然后各蚂蚁通过重复应用状态选择规则来选择各自的路径。在选路中,如果蚂蚁在到达目的节点前死亡,则应在初始点放出另一只来代替死亡的蚂蚁,重新开始选择从源节点到目的节点的路径.当一只蚂蚁成功地完成路由选择后,这只蚂蚁选择的路由的各路径上的信息素根据局部更新规则进行;
(3)nc←0;(nc为迭代步数或搜索次数),初始化各参数,即τij和Δτij的初始化,取消外激素,即以q0的比例选择最优路径,1-q0的比例选择其它路径,将m只蚂蚁置于个n节点上;
(4)将各蚂蚁的初始出发点置于当前解集中,根据蚂蚁的行进路线,对每个蚂蚁k(k=1,2,…m),计算其移动到下一节点j的概率,根据选择概率移动每只蚂蚁到下一节点,将节点j置于当前解集;计算时间却大大缩短,故直接采用取消外激素法所得最优解作为禁忌搜索的初始解;
(5)当m只蚂蚁遍历n个节点后,最优蚂蚁圈进行信息素增加Δ=Q/Zk计算各蚂蚁的目标函数Zk(k=1,2,…m),记录当前的最好解;

(7)进行重新的返回迭代或直到所有的负荷水平均被计算在内计算最优潮流,输出最优潮流、最优解、最优值和迭代次数,程序终止。
7 实例应用
为了验证智能蚂蚁算法的优化效果,现采用上述两种算法对30节IEEE点系统进行无功优化计算,并分析了系统节点数对智能蚂蚁算法性能的影响。由于原系统已经补偿过,电压质量能满足要求,网损也不大。现假设未补偿系统的功率因数为0.64,考虑对系统进行无功优化。假设系统中所有的变压器均为有载调压变压器,分接头每档为1.25%,无功补偿点设在各负荷点。包括6台发电机、4个无功补偿点。对其给定负荷状态下的无功功率进行了优化分配,其有功网损随着遗传代数的增加而减少,结果见表1。

表1 智能蚂蚁算法搜索结果
8 结论
日前,除了公认的遗传算法、模拟退火法、禁忌搜索法、人工神经网络等热门进化类方法,新加入这个智能蚂蚁算法为复杂困难的系统优化问题提供了新的具有竞争力的求解算法。本方法是在蚁群算法的基础上,提出了一种新的启发式搜索算法—智能蚂蚁系统智能蚂蚁系统通过对蚁群算法的改进,在减少计算量的同时,取得了令人满意的搜索结果实验结果表明,智能蚂蚁系统是解决分散性,无定性的问题的一种好方法。
(1)蚂蚁算法通过处理参数集合的编码,实现多途径搜索,给出全局意义上的最优、次优等多种优化方案;
(2)智能算法可称为是一种框架性的优化算法,计算过程中和原群蚁算法相比取消了外激素,计算和其外激素水平相差无几,可以避免重复搜索,也就达到了蚁群算法中局部更新的目的;
(3)由于采取多种措施,局部最优往往还是难以避免在智能蚂蚁系统中,通过扰动的引入使搜索跳出局部最优,达到全局的最优;
(4)蚂蚁算法以其特有的适应性,既解决了长期来困扰电力系统无功优化领域的变量的离散问题,又可避免维数灾难,找到全局最优解,较好地解决了电力系统无功优化问题。
[1]王锡凡.电力系统优化规划[M].北京:水利电力出版社,1990.5-20.
[2]赵登福,杨靖,刘显.基于改进遗传算法的配电网无功优化[J].西安交通大学学报,2001,35(12):1219 -1222.
[3]Luca Maria Gambardella,Marco Dorigo.solving Symmetric and Assymetric TSPs by Ant.Colonies[C].IEEE Conference on Evolutionary Computation,ICEC’96.
[4]Marco Dorigo,Vittorio Maniezzo,Alberto Coloni.Ant system:Optimizatio by a Colony of Cooperating Agents[J].IEEE Trana - actions on Systems,Man and Cybernetics,1996.
[5]倪炜,单渊达.具有优化路径的遗传算法应用于电力系统无功优化[J].电力系统自动化,2000,24(21):40 -44.
[6]杨毅刚,杨期余,杨维汉.电力系统优化的理论基础[M]北京:水利电力出版社,1988:140-182.
[7]熊信良,曹顺生.电力系统无功补偿最优配置非线性模型[C]//中国电机工程学会电力系统计算学会议论文集.大连,1990,11.
[8]朱太秀.电力系统优化潮流与无功优化[J].电网技术,1990,11(4).
[9]谢驰坤,陈陈.电力系统无功优化规划方法的研究[J].电力系统自动化,2000,12(5).

