电流跟踪数字控制的Buck DC-DC变换器

刘 健 程红丽 王 立 冷朝霞

(1. 西安科技大学电气与控制工程学院 西安 710054 2. 西安理工大学自动化与信息工程学院 西安 710048)

1 引言

近年来，在开关 DC-DC变换器的控制领域，取得了大量的研究新成果。

文献[1]探讨了具有最优动态响应的 PWM 型DC-DC变换器非线性控制新策略，文献[2]分析了PWM开关DC-DC变换器的低频波动的原因及波动参数，给出了避免低频波动的设计考虑。文献[3]分析了Buck DC-DC变换器的输出纹波电压与电感的参数关系。文献[4-5]探索了改进 DC-DC开关变换器的动态响应的控制新策略。文献[6-8]分别研究了采用V2控制、V2C控制和V2-OCC控制以提高变换器的动态响应速度的方法。文献[9]研究了采用滞环电流控制的双Buck逆变电路（HCDBI），消除了采用斜坡交截 SPWM控制的 DBI正常工作所必需的偏置电流。文献[10]研究了一种新的数字最优控制算法，以负载变化时动态性能最优为目标，将计算开关状态持续时间转化为对输出电压的控制，直接对占空比实行分段控制，提高动态响应速度。文献[11-13]研究了采用模糊控制和滑模控制能够改善PWM变换器的动态响应的方法。

数字控制具有低功耗、灵活多变、设计周期短、易实现模块化管理和集群控制，便于引入复杂和细腻的控制策略等优点，因此开关 DC-DC变换器的数字控制近年来成为研究者关注的新领域[14-15]。

文献[16-17]对数字控制的开关 DC-DC变换器的瞬态性能行了深入研究，提出了适合开关变换器的克服延时的算法，对于开关变换器的数字控制具有重要参考价值。文献[18]提出了一种根据变换器运行过程中电感电流的微分方程推导占空比的数字控制策略，采用数字PI技术进行稳态误差修正，并根据变换器输出电压与期望电压的偏差进行电流控制策略和带修正控制策略的切换控制。文献[19]提出了一种利用状态转移矩阵建立变换器的离散模型并求取最优化占空比的数字控制策略。文献[18-19]提出的开关 DC-DC变换器的数字控制策略仍是采用脉冲宽度调节，具有固定的开关频率，当负载较轻时容易工作在不连续导电模式（DCM），有时还需要工作在很低或很高的导通比下，不利于系统的调节和稳定。这些不足，不仅限制了开关变换器的输入工作电压范围和输出负载范围，而且降低了开关DC-DC变换器的动态响应性能。

随着微电子技术的发展，低电压器件的应用越来越广泛，对于降压变换器输出电流的要求也越来越高，并联均流技术成为研究的热点之一。

针对上述问题，本文提出一种基于微处理器的电流跟踪数字控制方法，它具有良好的稳态和动态工作特性，适合于进行智能并联均流控制。以Buck DC-DC变换器为例加以说明。

2 基本原理

2.1 基本组成

智能电流跟踪控制的Buck DC-DC变换器的组成如图1所示。

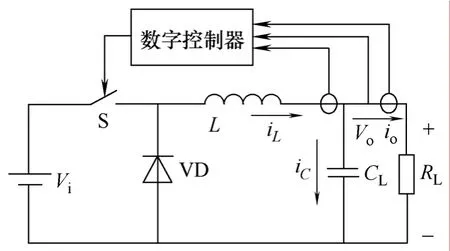
图1 电流跟踪数字控制的Buck DC-DC变换器的组成Fig.1 Structure of an intelligential current following controlled Buck DC-DC converter

与一般Buck DC-DC变换器不同的是，功率开关S的控制采用数字控制器，它根据对电感电流、输出电流和输出电压的采样信息来决定对功率开关S的控制。

2.2 基本控制原理

在连续导电模式（CCM）下，一个开关周期内流过电感电流的波形如图2所示，智能电流跟踪控制是根据智能控制器采集的电感电流iL(t)、输出电流io(t)和输出电压vo(t)，并实时计算出该变换器的负载电阻RL(t)，即

图2 电感电流及电流跟踪控制策略Fig.2 Illustration of the inductor current and the current following control

根据实时负载电阻RL(t)和期望达到的稳定输出电压VE，实时计算出所需要的平均输出电流Io(t)，即

设置一个电流滞环宽度ΔI，并采用下列控制策略（见图2a）：

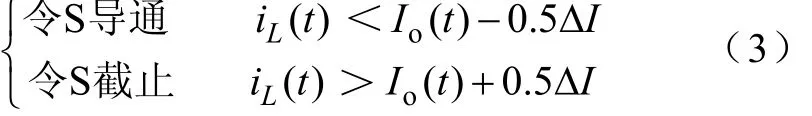
当负载较轻即输出电流较小时，有可能发生Io(t)-0.5ΔI＜0的情况，此时需要对式（3）的控制策略进行下列调整（见图2b）：

这样，在电流跟踪控制下，流过电感的平均电流就始终等于Io(t)，因此变换器的输出电压就可被稳定在期望达到的稳定输出电压VE=Io(t)RL(t)。并且，变换器在满足各参数设计限值要求的情况下总是工作在连续导电模式（CCM），而不会工作在不连续导电模式（DCM）。参数设计限值主要是指为了便于实现并避免过大的开关损耗而设置的最高开关频率限值，通常可以通过调整其他参数（如电感和电容）设计值来使最高开关频率限值满足要求，具体方法将在第4节详细论述。

本文提出的基于微处理器的电流跟踪数字控制的Buck DC-DC变换器，由于直接控制输出电流，因此非常适合于多个变换器模块并联组合进行智能均流控制实现大电流输出，并且各个模块的输出电流还可以根据其运行状态（如：发热情况）进行动态差异化分配，具体方法将另文专门论述。

3 分析

3.1 稳态分析

对于S导通的工作状态，有

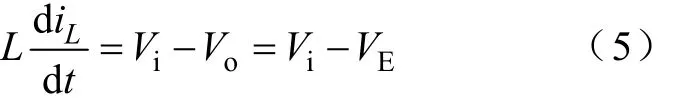
因此，S导通的工作状态的持续时间t1为

对于S截止的工作状态，有

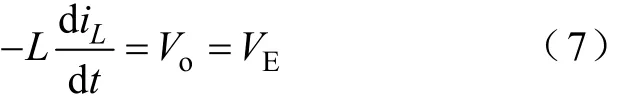
因此，S截止的工作状态的持续时间t2为

因此，对应图2a开关频率f为

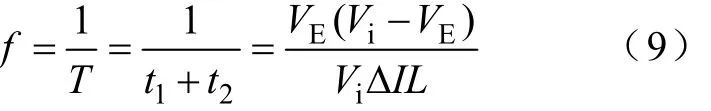
对应图2b开关频率f为

式中，T为开关周期。

由式（9）和式（10）可见，最低开关频率发生在输入电压Vi最低的情形，将Vi,min代入即可得出最低开关频率fmin。

导通比d为

可见，在负载不很轻的情况下，电流跟踪数字控制的Buck DC-DC变换器的开关频率仅仅取决于输入电压而与负载电阻无关（见式（9））；但是在负载很轻的情况下，智能电流跟踪控制的 Buck DC-DC变换器的开关频率不仅取决于输入电压而且还与负载电阻有关（见式（10））。并且与常规Buck DC-DC变换器一样，电流滞环数字控制的 Buck DC-DC变换器的导通比等于其输出输入电压比。

根据文献[20]，CCM Buck DC-DC变换器的输出纹波电压峰峰值ΔVPP为

将式（9）代入式（12）后，有

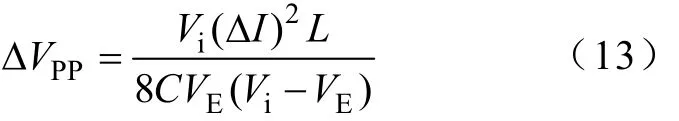
由于采用了电流跟踪控制，输入电压的突变不会对变换器输出电压的平均值产生任何影响。只对输出纹波有影响。

3.2 负载突降时的暂态分析

当负载突然从RL1减轻到RL2（即输出电流突然变小，从Io1突然减小到Io2）时，由于电感中的电流不能突变，因此输出电压有可能产生一定的“上冲”。考虑最坏的情况，即当输出负载突变时，电感电流刚达到最大值Io1+0.5ΔI。

在过渡过程中，当电感电流降低到Io2-0.5ΔI之前，S始终截止、VD始终导通。而传统的PWM控制因开关频率固定，在此期间需要经历许多以最小导通比工作的开关周期，而最小导通比大于 0，因此每个开关周期总要对电感补充一定的储能，其产生的输出电压“上冲”一定高于本文提出的智能电流跟踪控制，而且前者的“上冲”过渡过程持续的时间也较后者长。

过渡过程的微分方程为

这是一个关于输出电压vo(t)的二阶齐次微分方程，其初始条件为

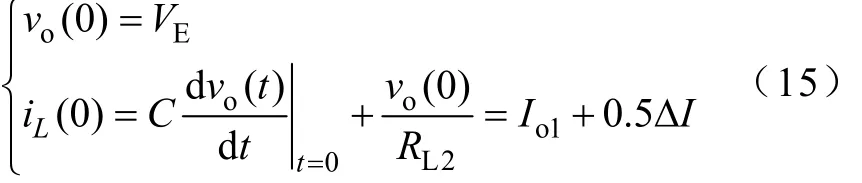
过渡过程中电感电流的表达式为

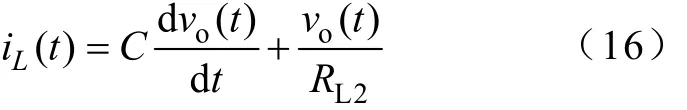
当电感电流降低到Io2-0.5ΔI之后，S导通，并且在智能电流跟踪控制下，流过电感的平均电流为Io2，也即交换的能量刚够满足RL2在输出电压为VE时所需的能量，因此当电感电流降低到Io2-0.5ΔI之后，输出电压不会进一步“上冲”，也即“上冲”的最大电压发生在电感电流降低到Io2-0.5ΔI之前。

因此，根据式（14）～式（16），可以得到在负载突变瞬间到iL(t)=Io2-0.5ΔI之间的vo(t)最大值，就是“上冲”的最大电压。

在最极端情况下，变换器由满载突然变为空载，则最大“过冲”电压Vo,max发生在电感的储能全部转化为电容的储能的时刻，即

3.3 负载突增时的暂态分析

当负载突然从RL2加重到RL1（即输出电流突然变大，从Io2突然增加到Io1）时，由于电感中的电流不能突变，因此输出电压会产生一定的“下冲”。考虑最坏的情况，即当输出负载突变时，电感电流刚达到最小值Io2-0.5ΔI。

在过渡过程中，当电感电流上升到Io1+0.5ΔI之前，S始终导通、VD始终截止。而传统的PWM控制因开关频率固定，在此期间需要经历许多以最大导通比工作的开关周期，而最大导通比小于1.0，因此其产生的输出电压“下冲”程度一定比本文提出的智能电流跟踪控制严重，而且前者的“下冲”过渡过程持续的时间也较后者长。

过渡过程的微分方程为

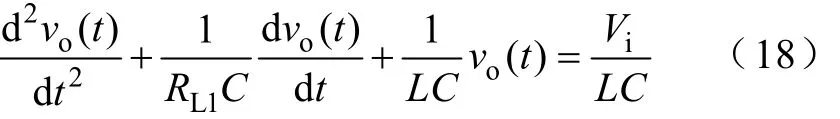
其初始条件为

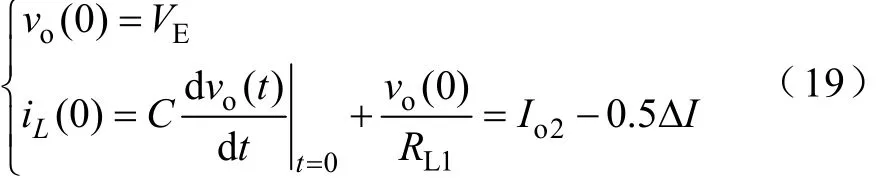
过渡过程中电感电流的表达式与式（16）相同，只是其中的RL2换为RL1。

当电感电流上升到Io1+0.5ΔI之后，S截止，并且在智能电流跟踪控制下，流过电感的平均电流为Io1，也即交换的能量能够满足RL1在输出电压为VE时所需的能量，所以此后输出电压不会进一步“下冲”，也即“下冲”的最低电压发生在电感电流上升到Io1+0.5ΔI之前。

因此，从负载突变瞬间到iL(t)=Io1+0.5ΔI之间的vo(t)最小值，就是“下冲”的最低电压。

在最极端情况下，变换器由空载突然变为满载，则电感电流达到Io1+0.5ΔI的时间ΔT近似为

从更加严峻的情况分析，忽略在此期间电感电流对电容的充电作用，则在ΔT内负载电流完全靠电容的储能维持，则最低下冲电压发生在负载突增后ΔT时刻，即

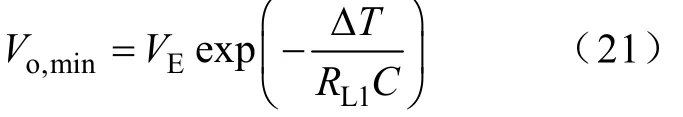
3.4 启动过程分析

在启动后，数字控制器迅速检测出负载电阻，并将电感的平均输出电流Io设置为所需的输出电流。由于在起动初始阶段电容的充电电流很大且电容电压（即输出电压）较低，因此在负载上的分流较小，流过电感的电流的大部分用于给电容充电。随着电容器电压越来越高，负载上的分流越来越大，用于给电容充电的电流则越来越小，因此电容电压的上升速度越来越慢。当电容电压（即输出电压）达到VE以后，流经电感的平均电流刚好能够满足负载的需要，因此电容电压不再增长。

综上所述可以总结出电流跟踪数字控制 Buck DC-DC变换器的启动过程具有下列特点：

（1）起动平稳，不会出现电压“过冲”。

（2）负载越轻则设置的电感平均输出电流Io越小，导致启动越慢。

（3）在负载很轻或者空载的情况下，需要设置一个基本的启动用电感平均输出电流，以缩短启动时间和避免启动困难，在电容电压达到VE以后再将电感平均输出电流设置回所需要的输出电流。但是这样做会导致启动时有少许电压“过冲”，最高“过冲”电压的分析可采用3.2节方法。

4 参数选择和设计考虑

在设计一个Buck DC-DC变换器时，通常Vi的范围（即Vi,min和Vi,max）、VE、RL,max（即Io,min）、RL,min（即Io,max）和输出纹波电压限值ΔVmax都已经给定，需要设计的参数包括：L、C和ΔI的取值。

由式（9）可见，输入电压Vi越高则开关频率越高，因此最高开关频率fmax为

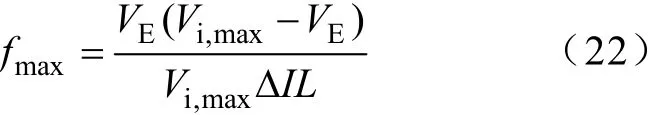
为了便于实现并避免过大的开关损耗，开关频率不宜太高，即fmax＜Fmax，一般Fmax可取 50～150kHz，则有

由式（13）可见，输入电压Vi越低则输出纹波电压越高，因此最高输出纹波电压ΔVPP,max为

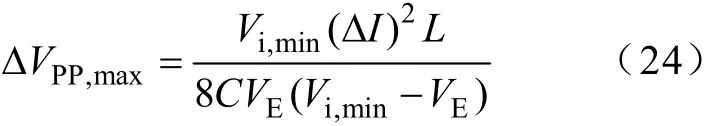
为了使ΔVpp,max＜ΔVmax，有

式中，μ为考虑到电容器的高频特性和分布参数后的保险系数，一般μ可取2～4。

为了确保极端情况下最大“过冲”电压不超过允许极限值Vmax，根据式（17），有

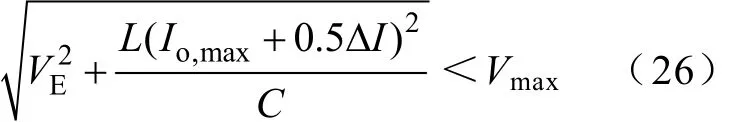
在负载突增时的暂态过程中，Vi越低则电感电流上升的速率越低，也即过渡过程越长，输出电压“下冲”越低。因此，在采用 3.3节方法分析最低输出电压“下冲”时，将输入电压取为Vi,min，并要求输出电压“下冲”大于允许极限值Vmin，即

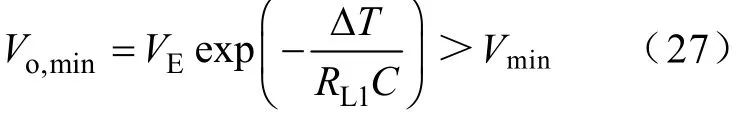
L、C和ΔI的设计值为符合式（23）和式（25）～式（27）设计范围的交集。由式（25）～式（27）看出，增大C对式（24）～式（26）的满足都有利，而式（22）与C无关。也即当上述交集（符合要求的设计范围）不存在或很小时，增大C是有效的解决途径。

5 实例

设计一台电流跟踪数字控制Buck DC-DC变换器，要求其输入电压范围为 DC8～25V，输出电压为DC 5V，输出负载电流范围为70mA～1A，输出纹波电压峰峰值小于 25mV，最大过冲电压小于5.2V，最低下冲电压大于4.8V。

根据输出负载电流范围，并且考虑到检测与控制的方便性，取ΔI=100mA。初步选取最高开关频率Fmax为60kHz，根据式（23）有

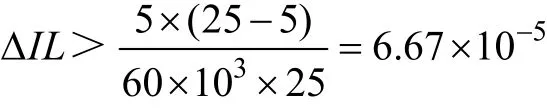
也即L＞667μH，取L=700μH。

取μ= 4，根据式（25）有

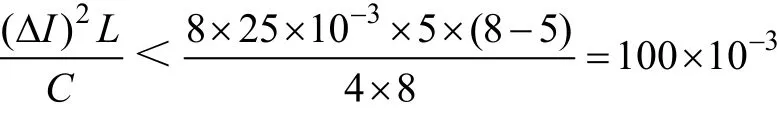
也即C＞75μF，取C=100μF。

将参数ΔI=100mA、L=700μH 和C=100μF 代入式（26）有

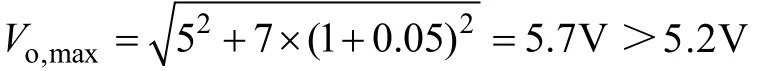
表明所设计的参数不符合要求，将C加大到660μF后再代入式（26）后得出最大上冲电压小于5.1V，小于所允许的5.2V，因此满足要求。

将参数ΔI=100mA、L=700μH 和C=660μF 代入式（20）和式（27）有

表明所设计的参数不符合要求，将C加大到1500μF后再代入式（27）后得出最低下冲电压大于所允许的4.8V，因此满足要求。

最终的设计参数为ΔI=100mA、L=700μH 和C=1500μF。根据式（22）可知，该变换器的理论最高开关频率为 57.14kHz；根据式（9）计算可知，该变换器的理论最低开关频率为26.78kHz，根据式（17）可知，该变换器的理论最高上冲电压为5.05V；根据式（21）可知，该变换器的理论最低下冲电压为4.84V。

采用ARM7—LPC2138作为数字控制器，并采用上述设计参数，研制了一台电流跟踪数字控制的Buck DC-DC变换器，实测最高开关频率发生在输入电压达到最高值25V时且不随负载变化而改变；最高开关频率为60.24kHz。实测最低开关频率发生在输入电压达到 8V最低值的情形；最低开关频率为 30.12kHz。

采用手动开关切换两个不同输出电压的电压源接入变换器的输入端的方法模拟输入电压突变。采用手动开关切换两个不同的负载电阻接入变换器的输出端的方法模拟负载电流突变。用数字示波器的触发功能捕捉突变发生时刻前后的波形。当负载电流从最大跳至最小时的最高上冲电压为 5.06V。当负载电流从最小跳至最大时的最低下冲电压为4.95V。输出最大纹波电压发生在输入电压最低时，为21.6mV。并且当输入电压突变时，输出电压不受影响。可见实验结果与理论分析一致。部分实验结果的波形如图3所示。

图3 部分实验结果的波形Fig.3 Some of the experimental results

6 结论

（1）电流跟踪数字控制Buck DC-DC变换器总是工作在连续导电模式（CCM）下，其开关频率是变化的。

（2）电流跟踪数字控制 Buck DC-DC变换器在输入电压突变、负载突变以及启动过程中具有较好的动态响应性能。

（3）实验结果表明，理论分析是正确的，电流跟踪数字控制方法是可行的。

[1] 许峰, 徐殿国, 柳玉秀. 具有最优动态响应的PWM型 DC-DC变换器非线性控制新策略[J]. 中国电机工程学报, 2003, 23(12): 133-139.

Xu Feng, Xu Dianguo, Liu Yuxiu. A novel nonlinear control method for PWM DC-DC converter with optimizing transient response[J]. Proceedings of the CSEE, 2003, 23(12): 133-139.

[2] 刘健, 王媛彬. PWM开关 DC-DC变换器的低频波动[J]. 中国电机工程学报, 2004, 24(4): 174-178.

Liu Jian, Wang Yuanbin. Low frequency ripple behaviour of PWM switching DC-DC converters[J].Proceedings of the CSEE, 2004, 24(4): 174-178.

[3] 刘树林, 刘健, 寇蕾, 等. Buck DC-DC变换器的输出纹波电压分析及其应用[J]. 电工技术学报, 2007,22(2): 91-97.

Liu Shulin, Liu Jian, Kou Lei, et al. Analysis of output ripple voltage of Buck DC-DC converter and its application[J]. Transactions of China Electrotechnical Society, 2007, 22(2): 91-97.

[4] 林维明, 黄是鹏, 张冠生, 等. 具有快速负载动态响应的 DC-DC开关变换器开环控制新策略[J]. 中国电机工程学报, 2001, 21(9): 78-81.

Lin Weiming, Huang Shipeng, Zhang Guansheng, et al. A new open-loop control strategy for a DC-DC switching converter with fast load transient response[J]. Proceedings of the CSEE, 2001, 21(9):78-81.

[5] 林维明, 黄是鹏, 张冠生, 等. PWM型DC-DC开关变换器非线性闭环控制策略的研究[J]. 中国电机工程学报, 2001, 21(3): 19-22.

Lin Weiming, Huang Shipeng, Zhang Guansheng, et al. Research on nonlinear control strategy for PWM DC-DC converters[J]. Proceedings of the CSEE, 2001,21(3): 19-22.

[6] Veerachary M. V2control of interleaved Buck converters[C]. Proceedings of the IEEE International Symposium on Circuits and Systems 2003, 3: 344-346.

[7] 王凤岩, 许建平. V2C控制Buck变换器分析[J]. 中国电机工程学报, 2006, 26(2): 121-126.

Wang Fengyan, Xu Jianping. Modeling and analysis of V2C controlled Buck converter[J]. Proceedings of the CSEE, 2006, 26(2): 121-126.

[8] 罗全明, 周雒维, 卢伟国, 等. V2-OCC控制Buck变换器[J]. 电工技术学报, 2008, 23(12): 78-83.

Luo Quanming, Zhou Luowei, Lu Weiguo, et al.V2-OCC controlled Buck converter[J]. Transactions of China Electrotechnical Society, 2008, 23(12):78-83.

[9] 洪峰, 刘军. 滞环电流控制型双Buck逆变器[J]. 电工技术学报, 2004, 19(8): 73-77.

Hong Feng, Liu Jun. Hysteresis current controled dual Buck half bridge inverter[J]. Transactions of China Electrotechnical Society, 2004, 19(8): 73-77.

[10] 徐海鹏, 周雒维, 孙鹏菊. 一种改善 DC-DC变换器动态性能的数字控制方式[J]. 电机与控制学报,2008, 12(4): 391-395.

Xu Haipeng, Zhou Luowei, Sun Pengju. Digital control method for improvement of DC-DC converter[J]. Electric Machines and Control, 2008,12(4): 391-395.

[11] 王伟, 易建强, 郑耀林, 等. DC-DC变换器的模糊神经网络控制方法研究[J]. 系统仿真学报, 2004,16(11): 2567-2574.

Wang Wei, Yi Jianqiang, Zheng Yaolin, et al. Fuzzy neural network control method for DC-DC converter[J]. Journal of System Simulation, 2004,16(11): 2567-2574.

[12] Ahmed M, Kuisma M, Tolsa K, et al. Implementing sliding mode control for buck converter[C]. 2003 IEEE 34th Annual Power Electronics Specialist Conference, 2003, 2: 634-637.

[13] Orosco R, Vazquez N. Discrete sliding mode control for DC-DC converters[C]. VII IEEE International Power Electronics Congress, 2000: 231-236.

[14] 郭唐仕, 陈锦云, 林龙凤, 等. 低功率开关电源的新型数字控制系统[J]. 电力电子技术, 2003, 37(1):63-65.

Guo Tangshi, Chen Jinyun, Lin Longfeng, et al. New digital control for low-power switching converter[J].Power Electronics, 2003, 37(1): 63-65.

[15] 韩智玲. 智能控制在 DC-DC变换器中的应用[J].电源技术应用, 2003, 6(11): 616-620.

Han Zhiling. Application of intelligent control in DC-DC converters[J]. Power Supply Techonlogies and Applications, 2003, 6(11): 616-620.

[16] 贺明智, 许建平, 郝瑞祥. 数字控制开关变换器瞬态性能的研究[J]. 四川大学学报(工程科学版),2009, 41(1): 185-189.

He Mingzhi, Xu Jianping, Hao Ruixiang. Study on transient performance of digital controlled switching converters[J]. Journal of Sichuan University(Engineering Science Edition), 2009, 41(1): 185-189.

[17] 贺明智, 许建平. 数字峰值电压控制开关变换器瞬态特性的研究[J]. 电力电子, 2008(4): 31-35.

He Mingzhi, Xu Jianping. Study transient performance of digital peak voltage controlled switching converters[J]. Power Electronics, 2008(4): 31-35.

[18] 冷朝霞, 刘健, 刘庆丰, 等. 一种新颖的 DC-DC变换器数字控制方法[J]. 西安理工大学学报, 2008,24(4): 421-425.

Leng Zhaoxia, Liu Jian, Liu Qingfeng, et al. A novel digital control for DC-DC switching converters[J].Journal of Xi’an University of Technology, 2008,24(4): 421-425.

[19] Leng Zhaoxia, Liu Jian, Liu Qingfeng, et al. A digital optimal control method for DC-DC converters based on simple model [C]. 2008 Workshop on Power Electronics and Intelligent Transportation System, 2008.

[20] 刘树林, 刘健, 寇蕾. 开关变换器的本质安全特性分析与设计[J]. 电工技术学报, 2006, 21(5): 36-41.

Liu Shulin, Liu Jian, Kou Lei. Intrinsically safe behavior of switching converters and its design[J].Transactions of China Electrotechnical Society, 2006,21(5): 36-41.

[21] 邹雪涛, 蔡丽鹃. 开关变换器中数字控制设计方法的研究[J]. 通信电源技术, 2006, 23(6): 19-21.

Zou Xuetao, Cai Lijuan. Study on digital control approaches in switching mode converter[J]. Telecom Power Technologies, 2006, 23(6): 19-21.