三层并行遗传算法及装箱问题中的应用*

张丽岩 ，马 健 ，孙 焰

(1.同济大学 交通运输工程学院，上海 201804；2.苏州科技学院 土木工程学院，江苏 苏州 215011)

近两年来，随着超线程处理器和多核处理器技术的出现及广泛应用，基于多核的并行计算成为新的研究热点[1-2]。多CPU多核计算机采用称为对称多处理器SMP(Symmetrical Multi-Processing)的数据处理结构，这种结构特别适合需要大内存、高性能CPU计算能力的应用场合，能够满足大型科学计算及实时信息处理的需要。从系统性能来看，SMP的通信时间比Cluster大大减少。尽管今天主流计算机仍然是基于单CPU双核的芯片技术，相信不久将来，单CPU 4核、8核乃至 16核的计算机将会到来，单机多CPU、多核高性能计算技术必将成为主流。

本文旨在提出一种基于多核SMP结构的三层并行遗传算法 TPGA(Three-tier Parallel Genetic Algorithm)，并基于线程构建模块TBB(Threading Building Blocks)，采用C++实现了这种算法。并采用装箱问题来验证TPGA的正确性及有效性，同时对TPGA进行了优化，以加快收敛速度，提高解的质量，充分发挥了多核SMP计算机的性能。

1 线程构建模块

1.1 线程构建模块简介

TBB是一个开源的C++模板库，它可将线程抽象成任务，然后创建可靠、可移植且可扩展的并行应用程序。使用TBB编写基于任务的并行应用程序，有助于提高跨多核平台上运行的可扩展软件的开发效率。与本地线程和线程封装器(wrapper)等其他线程化方法相比，它能够充分利用多核平台的并行性能[1-3]，是执行并行应用程序最高效的方式，TBB有以下三个显著的优点[2]：(1)TBB对线程进行抽象，将其提高到任务的高度，简化了并行应用程序的开发工作；(2)基于TBB开发的应用程序的性能，可以随着处理器内核数量的增加而自动提升；(3)TBB能够减少死锁和资源竞争等常见线程错误，提供了一个跨平台的并行解决方案。本文采用C++实现了基于TBB的 TPGA和 SGA(Sequential Genetic Algorithm)，充分利用了TBB的高效性、可靠性和可扩展性[1-5]。

1.2 TBB[1]的特性

对于开发者来说，TBB有以下明显的好处：(1)TBB大大减少了开发多线程并行应用程序所需的代码行数，它的任务抽象模型节省了大量的开发时间；(2)TBB屏蔽了抽象线程管理的许多细节，大大降低了开发多线程应用程序的复杂性；(3)基于TBB的多线程程序在运行时，其任务管理器会自动分析运行环境，并根据实际情况选择最佳的线程数量(在程序的参数限制范围内)，使系统在所有的处理器上保持最佳的负载平衡。因此，TBB多线程应用程序能够自动调整线程规模，充分利用一切可用的多核处理器资源，发挥多核平台的并发优势，提高程序的运行效率。线程库的功能比较如表1所示。

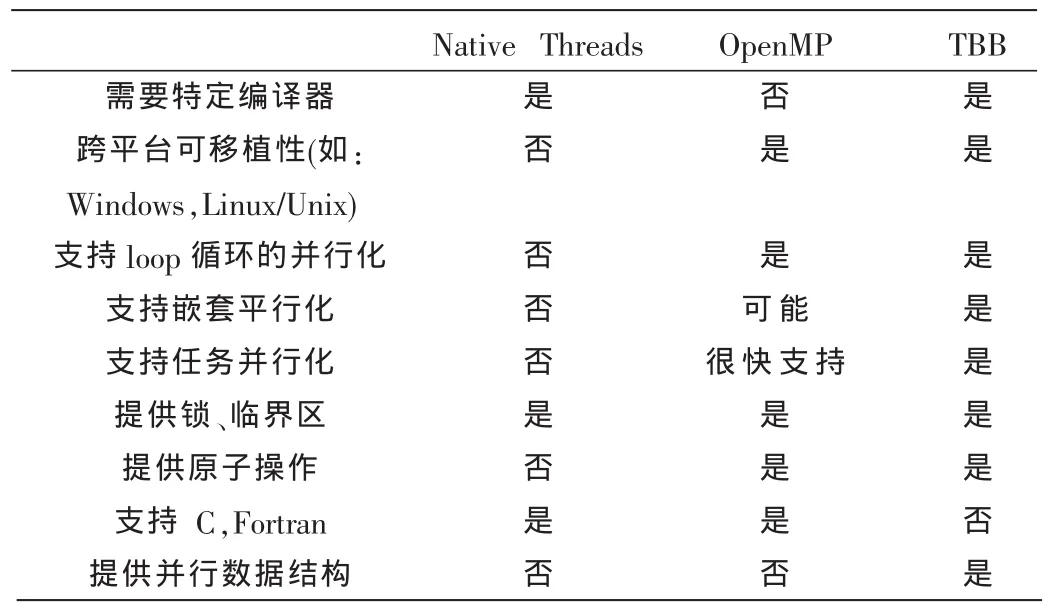
表1 线程库的功能比较

2 并行化思维

2.1 串行算法并行化

一般情况下，设计并行算法有三种策略[4-5]：(1)分析现有串行算法中的并行性，并直接将其并行化；(2)从问题本身出发，根据问题固有的并行性，设计一个全新的并行算法；(3)借用已有的并行算法求解新的问题。

目前，串行算法的发展已经比较成熟，在设计并行算法时要充分加以利用，并尽量在其基础上直接并行化，或者将其内嵌在其他并行算法中。本文采用第二种策略将串行遗传算法(SGA)内嵌于TPGA算法中，使之能更好地利用多核计算机的并行处理能力，加快算法的收敛速度，提高解的质量。

2.2 数据并行性与任务并行性

在并行算法的具体实现中大多先采用划分技术，即将一个问题划分为许多子问题，这些子问题彼此独立但又密切相关，然后将它们分派给不同的线程或进程，并在不同的处理器上执行，最后，采用合并技术将不同线程或进程得到的结果进行合并。在一个具体的实际问题中，并行性的存在形式可以是并行操作的数据或者是并发执行的任务。如果给定一个数据集合，对在此集合中的每个元素都执行相同的操作，那么就可以并发地在每个元素上执行相同的任务[3-5]。

图1是数据并行性的示例图，表明如果给定一个数据集合以及集合中的每一个元素都执行相同的操作，利用数据并行性，就可以并发地在每个元素上执行相同任务。图中CAP为小写转大写运算。

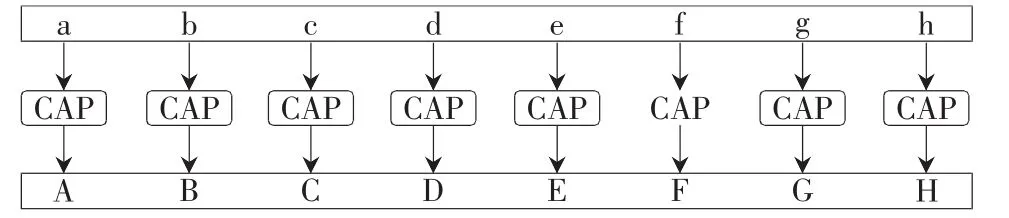
图1 数据并行性的示例图

任务并行性指的是大量通过共享数据被关联在一起的不同任务。图2是任务并行性的示例图，图中以一些数学运算为例，其中每个运算都可以应用到相同的数据集合上以计算独立的值。图中AVERAGE为求平均值；MINIMUM为求最小值；BINARY OR为求二进制“或”；GEO-MEAN为求几何平均。

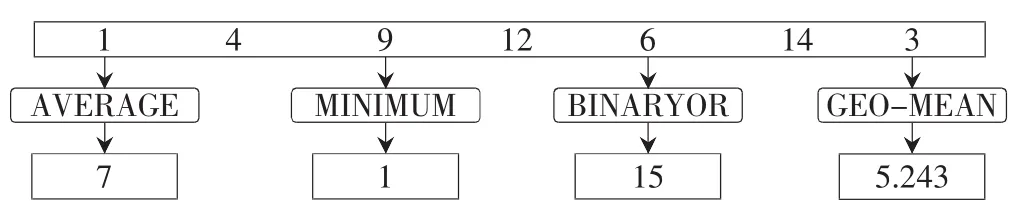
图2 任务并行性的示例图

数据的并行性受限于所要处理的数据，包括数据规模、数据类型、数据存储格式等，而任务的并行性是将不同的任务通过数据共享关联在一起并发执行。纯粹的任务并行性要比纯粹的数据并行性更难发现。本文采用三层架构，集成了数据的并行性和任务的并行性，更易于TPGA的并行实现。

3 三层并行遗传算法

3.1 并行遗传算法

遗传算法GA(Genetic Algorithm)是近几年发展起来的一种崭新的全局优化算法，它借用了生物遗传学的观点。在计算机中，通过对自然选择、遗传、变异等作用机制的模拟，实现提高各个个体的适应性。

遗传算法是从代表问题可能潜在解集的一个初始种群开始的，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解。在每一代，根据问题域中个体的适应度大小挑选个体，并借助自然遗传学的遗传算子进行组合交叉和变异，产生出代表新解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题的近似最优解[6-7]。

虽然遗传算法已经成功地应用在许多领域，且能在合理的时间内找到满意解，但随着求解问题的复杂性及难度的增加，提高GA的运行效率显得尤为重要，采用并行遗传算法PGA(Parallel Genetic Algorithm)是提高运行效率的方法之一。由于GA以种群为出发点，具有天然的并行特性，非常适合并行实现，而多核计算机的日益普及，为PGA奠定了物质基础。GA中各个体适值计算可独立进行且彼此间无需通信，所以并行效率很高。

实现PGA，重要的是对SGA的结构进行分析，发现结构中的数据并行性及任务并行性，把SGA等价地变换成一种并行方案，形成并行种群模型。并行种群模型对传统SGA的修改涉及到两个方面：一是数据并行化，即将SGA的单一种群分成多个子种群，分而治之；二是任务并行化，即控制、管理子种群之间的信息交换及种群内部的操作。不同的分治方法产生不同的PGA结构。这种结构上的差异导致了不同的PGA模型，即全局并行模型、粗粒度模型、细粒度模型[8]。

3.2 TPGA的框架

为了集成数据的并行性和任务的并行性，本文采用三层架构，实现了TPGA。(1)第一层是数据编码并行化。分析输入数据的特点，包括数据类型、存储形式、数据规模等，找出其中的并行性，进行数据分解、数据编码，以得到适合任务并行执行的数据编码及数据模块。(2)第二层是任务处理并行化。将经过分解的数据模块及数据编码传入SGA，各个SGA并发的执行，得到各自的适应函数值。(3)第三层是数据解码并行化。将各个SGA得到的值传给数据整合模块，经过并行化处理，得到最优解。图3是TPGA的通用框架[9]。

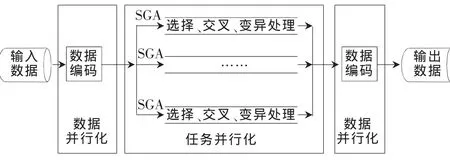
图3 TPGA的通用框架

4 在装箱问题中对TPGA的验证

装箱问题是一个典型的组合优化问题，其属于NP完全问题，这类问题不存在有效时间内求得精确解的算法，所以装箱问题的求解极为困难。一般采用启发式算法求解此类问题。

本算例主要研究的是抽象意义下的装箱问题，可以描述为给定的箱子及物品(设物品的尺寸小于箱子的尺寸，且为规则物体)，目标是设计一种方案，将所有物品装入箱子而使箱子的利用率最高。在这里，假设物品的摆放方向不受约束，稳定性及装载的均匀性等暂不考虑[10]，主要考虑箱子的最大载重量、承载能力等。将上述TPGA思想应用到装箱问题中，并利用罚函数法改造目标函数来解决装箱问题，其模型如下：

设m为某一装箱方案中所用箱子的数目，B(ui)为物品ui所装入箱子的编号，sj为考虑了罚函数之后的Bj箱所装物品的体积之和。要使所用箱子数目最少，可以取下式为优化目标函数：

式中，α为某一箱子Bj中所装物品的体积之和超出箱子规定容积时的惩罚因子，α＞0。

该目标函数既考虑了使所用箱子的数目最小，又考虑了使每个箱子装完物品后所剩余的容积尽可能小。

图4为TPGA的求解装箱问题示意图。

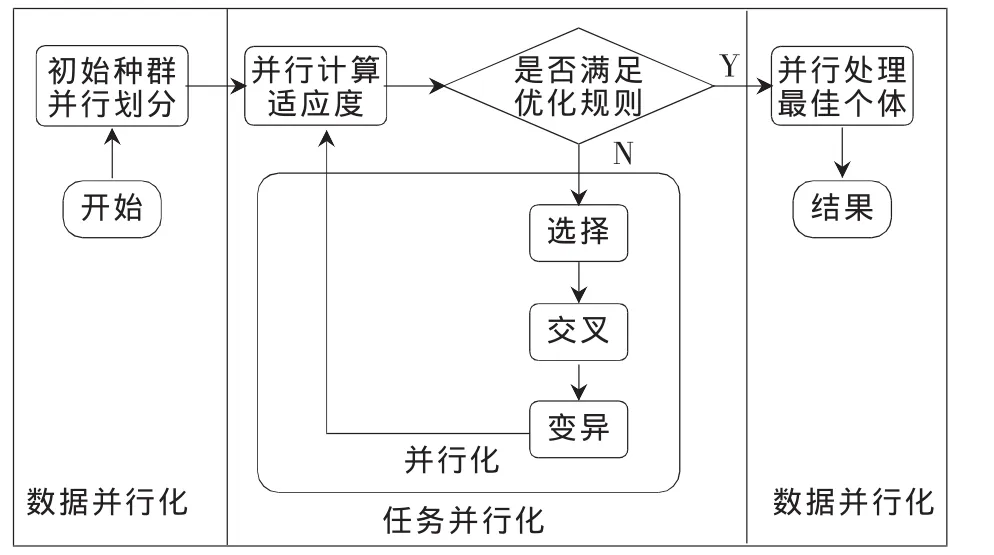
图4 TPGA流程图

5 TPGA与SGA的对比

5.1 TPGA的有效性验证

在本算例中，假设箱子的体积为1(箱子长、宽、高均为 1)，箱子的数量为 18(根据物品个数而定)，初始群体大小为18，染色体长度为 18(根据物品个数决定)，算法迭代次数视具体情况而定。通过调节算法中的惩罚因子α、交叉概率pc、变异概率pm三个主要参数，确定了以惩罚因子 α=0.45，交叉概率 pc=0.8，变异概率 pm=0.001来进行遗传算法的计算。将其迭代5 000次，不同算法的结果对比如表2所示。

表2 TPGA与SGA的装箱方案对比

由表2可以看出，SGA总共用了10个箱子且箱子的平均利用率为70.2%；而TPGA总共用了9个箱子且箱子的平均利用率为81.3%；TPGA要明显优于基本遗传算法SGA。

5.2 TPGA的效率性验证

为了更好地比较实验结果，应在同一平台下进行实验，本文的实验平台具体配置为：CPU为Intel Pentium Dual-Core(Merom)T3400(2.16 GB)；内存 2 048 MB；操作系统为 Windows XP(sp2)。

图5给出了不同箱子的规模 (染色体长度规模)，不同线程数目与收敛速度的对应关系。通过比较分析，得到此情况下的最优线程数和全局最优解。与此同时，分析比较TPGA与SGA的运行效率及收敛速度。

由图5可以看出，当线程数目为1时 (此时即为SGA)，随着箱子规模的增大，系统的运行时间明显增大很多，收敛速度较慢；当线程数目为128时 (此时即为TPGA)，此时的子矩阵为 32，随着箱子规模的增大，系统的运行时间有所增加，收敛速度较快。通过两者对比，当线程数目增加到一定程度时，可以明显看出，TPGA的运行时间要明显小于SGA的运行时间。可见，当箱子规模较大时，TPGA要明显优于SGA。

图5 线程数与收敛速度关系图

本文提出了TPGA，并用于解决装箱问题。经实验证明，TPGA明显优于SGA，且在解的优化程度和收敛速度上均有显著提高，并对TPGA进行了优化。当惩罚因子α=0.45，交叉概率 pc=0.8，变异概率 pm=0.001，线程数目为128，子矩阵为32时，TPGA能够取得相对较好的解。此时收敛速度较快，并且解的优化程度较高。

TPGA还可应用于有大量计算机节点的分布式系统，及算法参数的进一步优化等，以进一步提高解的质量及收敛速度。同时，TPGA也可以应用于其他领域，如物流的选址问题、交通路径选择问题等。

[1]http：//www.threadingbuildingblocks.org/[OL].

[2]REINDERS J.Intel threading building blocks outfit-ting C++for multi-core processor parallelism[M].First Edition，O′Reilly Media， Inc.， 2007.

[3]刘勇，等.非数值并行算法—遗传算法[M].北京：科学出版社，1995.

[4]BLAKE C L，MERZ C J.UCI repository of machine learning databases[DB/OL]. http：//www.ics.uci.edu/～mlearn/MLRepository.htm，2003.

[5]LIANG J Y，CHIN K S，DANG C Y，et al.A new method for measuring uncertainty and fuzziness in rough set theory[J].International Journal of General Systems， 2002，31(4)：331-342.

[6]王小平，曹立明.遗传算法——理论、应用与软件实现[M]，西安：西安交通大学出版社，2002.

[7]陈鹏.并行遗传算法初始种群划分建模与设计[J].计算机工程与应用，2004(7)：78-79.

[8]崔明义.并行遗传算法在工程智能优化中的实现策略[J].计算机工程与应用，2004(7)：90-91.

[9]Ma Jian， Li Keping， Zhang Liyan.The adaptive parallel simulated annealing algorithm based on TBB[C]，The 2nd IEEE InternationalConference on Advanced Computer Control，2010.

[10]张丽岩.装箱问题BFD混合遗传算法的仿真研究[D]，南京：河海大学，2006.