Variable-mass Thermodynamics Calculation Model for Gas-operated Automatic Weapon

CHEN Jian-bin(陈建彬)，LV Xiao-qiang(吕小强)

(Unit No.77298，Qvjing 655000，Yunnan，China)

Introduction

The gas-operated automatic weapon acts automatically by using the propellant gas of high pressure and temperature from gas hole of the barrel to push the automatic machine，and the proper use of gunpowder gas is greatly important to the dynamic performance of the automatic weapons［1］.Therefore，the study on the dynamic characteristics of the gas-operated device is very significant for using propellant gas and obtaining favorable dynamic characteristics.Most oversea studies on the dynamic characteristics of automatic weapons are based on the experience methods，such as Bradley method，Mamun Rostov method，Brad Gongla Wolf method，and so forth.Domestic research work primarily focuses on two aspects.One is introduction of foreign experience models［2］and establishment of numerical models based on the formers［2－3］.By using the numerical models，many parameters can be solved more accurately;compared with the empirical models.The other is improvement and application of the models.The research improved the models in references［1－3］，and then applied it to the metal storm weapon system’s ballistic consistency［4］，optimal design of gasoperated devices［5－6］.But，obviously，in all references existing before，it can be found that，the establishments of both numerical and empirical models do not consider the variable-mass thermodynamic process between interior ballistics and gas-operated device，and the models have too many equations，parameters and biggish error.In all applied researches，the coupling of the interior ballistics and the gas-operated device is not considered in the improved model.Therefore，in order to overcome above deficiencies and explore the methods of accurately predicting the performance and determining the structural parameters of the gas-operated automatic weapon，by analyzing the thermodynamic process between the barrel and gas-operated devices，the variable mass thermodynamic calculation model，which is more objective and accurately describing the process of gas-operated automatic weapon firing，should be established.

1 Variable-massThermodynamics Model of Gas-operated Automatic Weapon

1.1 Physical Process and Basic Assumptions

The typical structure of gas-operated automatic weapon is shown in Fig.1.After the hammer hits the primer，the propellant starts burning，and the bore pressure increases rapidly.When the pressure at the bottom of the projectile becomes greater than the squeeze pressure，the projectile begins to cut into the rifle and accelerates.With the gunpowder combustion and the space behind the projectile increase，the pressure at the projectile bottom gradually decreases.When the projectile goes over the gas-operated hole，the propellant gas begins to flow from the gas chamber into the guiding hole.For the bore pressure is much larger than the guiding hole pressure in the beginning，the gas flow near the hole appears in a positive critical sonic flow.With the propellant gas flowing into the guiding hole increases，the pressure increases，and the gas flow near gas hole becomes non-critical sonic flow.Then，the projectile moves forward continuously，and the piston moves backward.When the gas force acting on the piston end and the resistant force of the recoil spring are equal，the piston speed reaches the maximum，and then the bore pressure reduces further.When it becomes smaller than the guiding hole pressure and their ratio does not exceed a certain value，the propellant gas in guiding hole begins to flow into the barrel，and the gas flow near the guiding hole becomes reverse non-critical sonic flow.When the ratio exceeds a certain value，the reverse gas flow near the guiding hole becomes critical sonic flow.When the projectile exits the muzzle，its motion enters the aftereffect period，and the propellant gas sprays at extremely high speed.For its flow velocity and pressure are very high，the projectile is still accelerated.With the increase of projectile displacement，the velocity of projectile decreases gradually，and the bore pressure decreases also.At the end of the aftereffect period，the velocity of projectile reaches its maximum.

Basic assumptions:

1)The classical model is employed to describe the ballistic process;

2)The flow in gas-operated device is a variablemass thermodynamic process with flow-in and flow-out;

3)The heat exchange among the propellant gas，barrel and gas chamber is ignored，for the transient calculation;

4)The gas-operated device and interior ballistics are coupled through the flux of propellant gas.

1.2 Computational Model

The variable-mass thermodynamics computational model of gas-operated automatic weapon includes interior ballistic model，gas chamber model and coupled equations.They are listed as follows.

Equation of bore pressure:

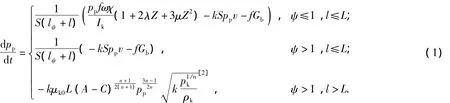
wherepp，S，lψ，l，f，ω，Ik，Z，k，ν，Gb，μk0，pk，ρk，L，n，ψare gas chamber pressure，cross-sectional area of barrel，chamber length，bullet displacement，gunpowder force，charge amount of propellant，gas pressure’s whole impulse，relative thickness of the powder fired，adiabatic index，bullet velocity，gas flow，at gas-operated hole，muzzle flow coefficient，muzzle gaspressure， muzzle gasdensity， barrel length，change index，percentage of gunpowder fired，respectively.AandCare constants related to the change index.χ，λandμare shape coefficient of gunpowder.

Equation of proportional burning rate［7］:

Equation of geometric combustion［7］:

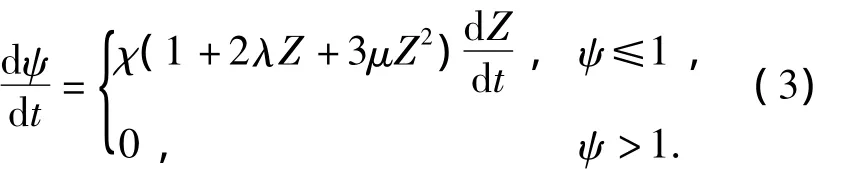
Motion equation of bullet［7］:

Velocity equation of bullet［7］:

whereφis the secondary power coefficient，mis the bullet mass.

Mass equation of gas flowed out through guiding hole:

whereηis the gas mass flowed from barrel.

Equation of reduced diameter of chamber’s free volume［7］:

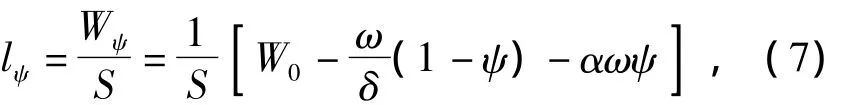
whereW0is the initial volume of chamber，δis the powder density，αis the residual volume.

Density equation of gunpowder gas inbarrel:

whereρpis the gas density of gunpowder in barrel.

Equation of gas pressure in gas chamber［2］:

wherepq，γ，Vq，Vq0，Sh，vh，paare bore pressure，specific heat ratio，chamber volume，initial volume of chamber，piston’s cross-sectional area，piston velocity and atmospheric pressure，respectively.

Flow equation in piston clearance［2］

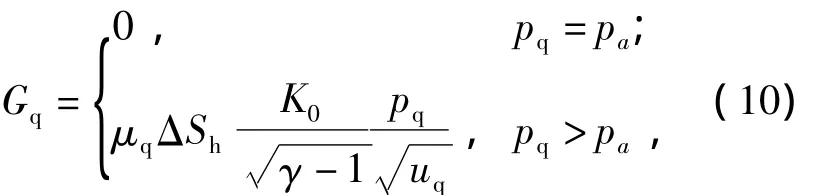
whereGq，ΔSh，μq，γanduqare gas flow in piston clearance，gap area of piston，flow coefficient of gas chamber，specific heat ratio，gas internal energy per unit mass，respectively，K0is the constant related toγ.

Mass equation of gas in chamber［2］:

wheremqis the mass of propellant gas in chamber.

Motion equation of piston:

whereK，xh，B，mhare buffer spring stiffness，piston displacement，actuator friction resistance and piston mass，respectively，andF=(pq－pa)Sh－Kxh－Bis the total force applied to the piston.

Displacement equation of piston［2］:

Mass conservation equation in gas chamber:

whereρqandlkare the density and location of gas hole.

Internal energy equation of unit gas mass in chamber［2］:

Coupling equation［1－2］:

The interior ballistics and gas-operated device are coupled with the flow equation.

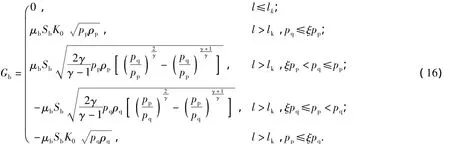
2 Model Verification and Calculation Results

2.1 Model Verification

Fig.2 shows the experimentalv-tcurve of automatic mechanism of an automatic weapon.In order to verify the correctness of the model，it is adopted to calculate the dynamic parameters of the weapon，by using fourth-order Runge-Kutta method in MATLAB.And the variation of the recoil speed of automatic mechanism in the initial phase is obtained，then，it is compared with the experimental result，as shown in Fig.3.It can be seen that the theoretical speed is zero in that phase，as the effect of recoil force acting directly on the bottom of projectile on the speed of automatic mechanism is ignored.When the propellant gas pushes the piston and then causes the automatic mechanism to move backward，the calculation result coincides with the experiment result better，and the maximum recoil speeds are accordant.It shows that the variable-mass thermodynamic calculation model of gas-operated automatic weapon established in this paper is accurate and reliable.

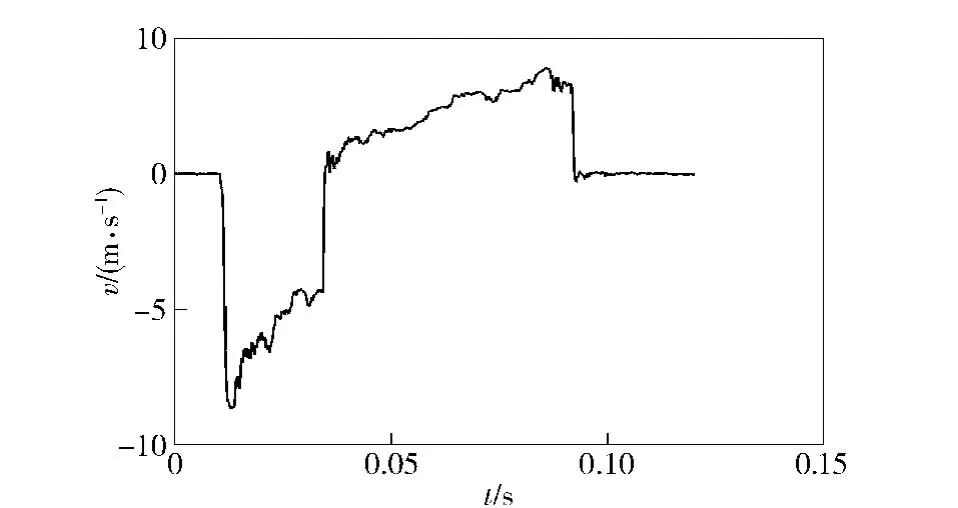
Fig.2 v-t curve of automatic mechanism

Fig.3 v-t in initial recoil phase

2.2 Calculation Results Analysis

2.2.1 Flow Flux at Gas-operated Hole

The flow flux at gas hole of a certain gas-operated automatic weapon is shown in Fig.4.When the bullet reaches to the gas-operated hole，the bore pressure is relative high，while the pressure in gas-operated device is only one atmosphere，so the positive critical flow appears at the hole，and the flow flux increases to 1.16 kg/s instantly;then the flow flux begins to decline.When the bullet leaves the muzzle，the propellant gas sprays out quickly，and the bore pressure drops rapidly，so the positive non-critical flow appears at the hole.When the bullet continues to move，the bore pressure declines further，and then the pressure in gas-operated device becomes higher than the bore pressure，so the reversed non-critical flow appears at the hole and the maximum flow flux is about 0.18 kg/s.With the propellant gas flows into the chamber，the pressure in gas-guiding device declines gradually，and the flow flux decreases to zero finally.

Fig.4 Gas flux

2.2.2 Influence of Coupling on Chamber Pressure and Muzzle Velocity

Fig.5 compares the bore pressures considering and not considering the coupling effect.It can be seen that the difference of the bore pressures is less at the beginning and end of the phase from the bullet moving to the gas hole and the aftereffect period，while the difference is relatively large in the middle of the process.When the bullet exits the muzzle，the pressure difference reaches the maximum of 6.7 MPa.Fig.6 shows the projectile velocity curve without the effect of coupling.It can be seen that the influence of coupling energy on the velocity is obvious，and the influence on the shell leaving speed is about 6 m/s.At the end of aftereffect period，the influence on the speed reaches the maximum of 16 m/s.Thus，it can be seen that the propellant gas flowing into the gas-operated device has a certain influence on the bore pressure and projectile velocity，and the influence of coupling energy on the bore pressure and projectile velocity should be considered when solving the interior ballistics and the dynamics of gas-operated device.

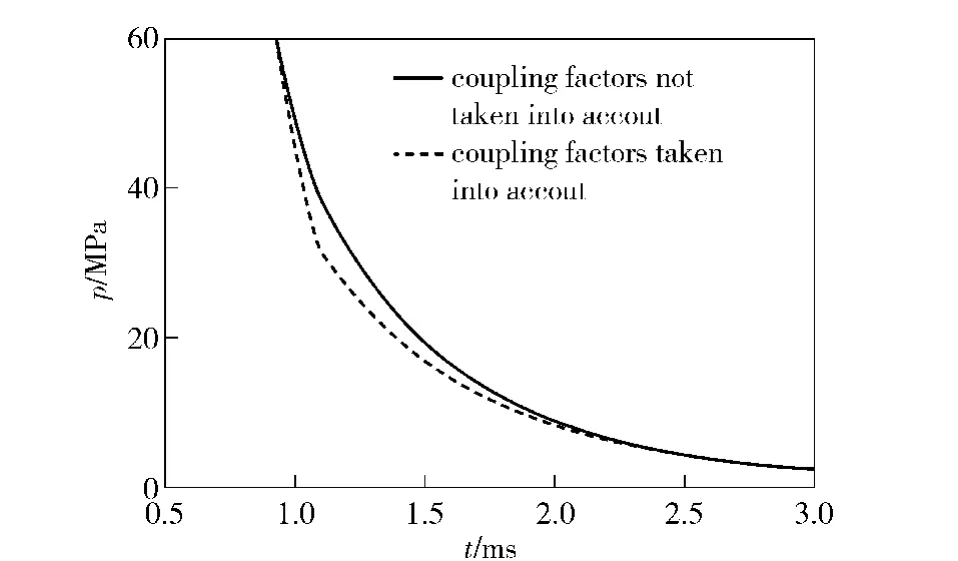
Fig.5 Influence of coupling energy on bore pressure

2.2.3 Influence of Initial Volume of Gas-operated Device

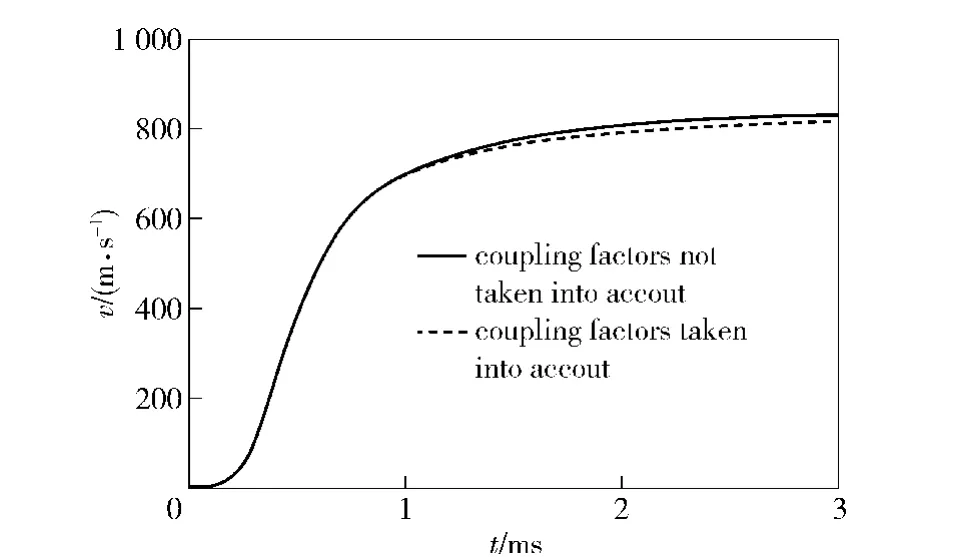
Fig.6 Influence of coupling energy on bullet speed

The influences of the initial volume of gas chamber on the pressure in gas-operated device and the maximum recoil velocity of automatic machines are shown in Fig.7 and Fig.8，respectively.When the initial volume of the gas chamber is 1.7 ×10－6m3，the theoretical maximum pressure is 23.7 MPa，and the maximum recoil velocity of automatic machine is 8.61 m/s.If the initial volume is 2.2×10－6m3or 2.7 ×10－6m3，the maximum pressure is 21.4 MPa or 19.7 MPa，and the maximum recoil speed is 8.38 m/s or 8.24 m/s.Thus，it can be seen that，with the initial volume’s increase，the pressure in gas chamber reduces and the pressure peak delays and the maximum recoil speed reduces also.In addition，the acceleration of pressure decreasing reduces.It shows that the initial volume of gas chamber has impact on the bore pressure，the appearance time of maximum pressure and the velocity of automatic machines.In other words，in the gas-operated device design，the pressure，the emergence time of maximum pressure and the recoil speed can be adjusted by changing the initial volume of gas chamber.

Fig.7 Influence of initial volume on gas chamber pressure

2.2.4 Gap’s Effect on Gas-operated Device

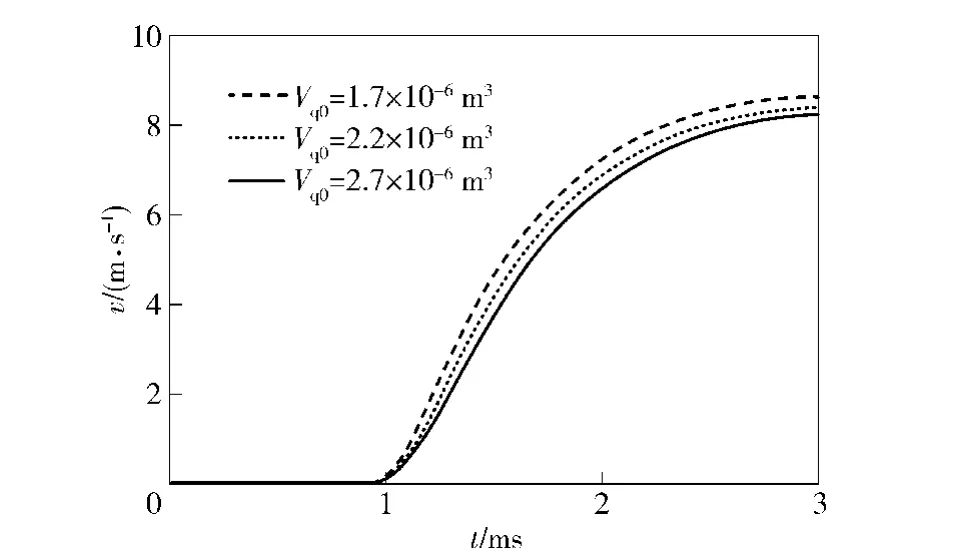
Fig.8 Influence of initial volume on automatic mechanism speed

The influences of gas chamber’s gap on the automatic machine recoil velocity and gas chamber pressure are shown in Fig.9 － 10，respectively.If the gap measures 0.1 mm，the maximum pressure in the gas chamber is 23.7 MPa，and the maximum recoil speed of automatic machine 8.61 m/s.If the gaps are 0.5 mm and 1 mm respectively，the maximum pressures are 23.2 MPa and 21.4 MPa，and the maximum recoil speeds are 8.48 m/s and 8.18 m/s，respectively.It shows that the gap less than 0.5 mm influences on the gas chamber pressure and maximum recoil speed a litter.While the gap is increased to 1 mm，the pressure of gas chamber reduces by 1.8 MPa compared with the gap of 0.5 mm，and the maximum recoil speed reduces by 0.3 m/s.It shows that the gap variance between 0.5 mm and 1 mm has obvious effect on the pressure of gas chamber and maximum recoil velocity.However，the emergence time of peak pressure keeps no change，which indicates that the gap design as between 0.1 mm and 0.5 mm is appropriate.

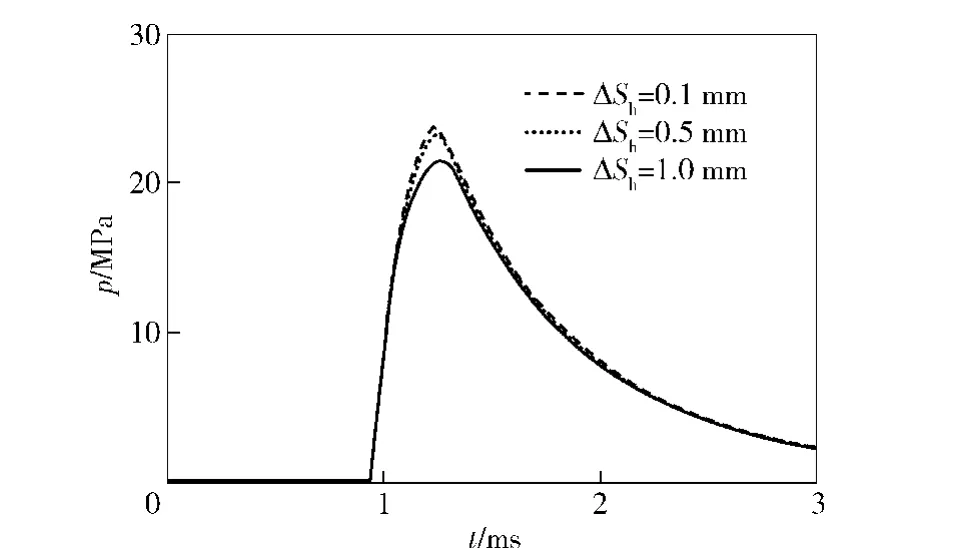
Fig.9 Influence of clearance on gas chamber pressure

2.2.5 Influence of Hole’s Diameter on Gas-operated Device

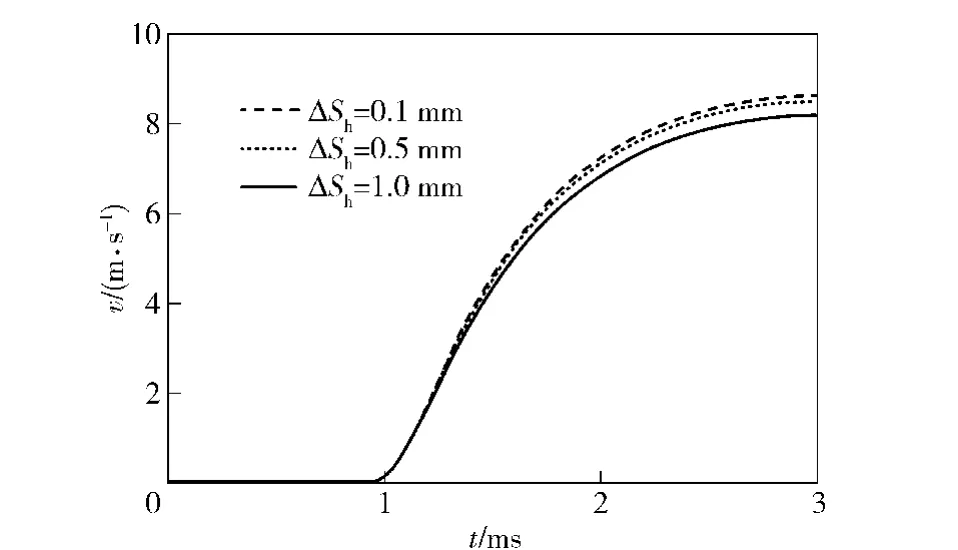
Fig.10 Influence of clearance on automatic mechanism speed

The influences of the gas-operated hole’s diameter on the gas chamber pressure and the recoil velocity of automatic machine are shown in Fig.11 － 12，respectively.With the increase of hole’s diameter，the pressure in gas chamber and the recoil speed of automatic machines increase.When the diameter of gas hole varies around a smaller value，the pressure of gas chamber and the maximum recoil velocity are more sensitive.

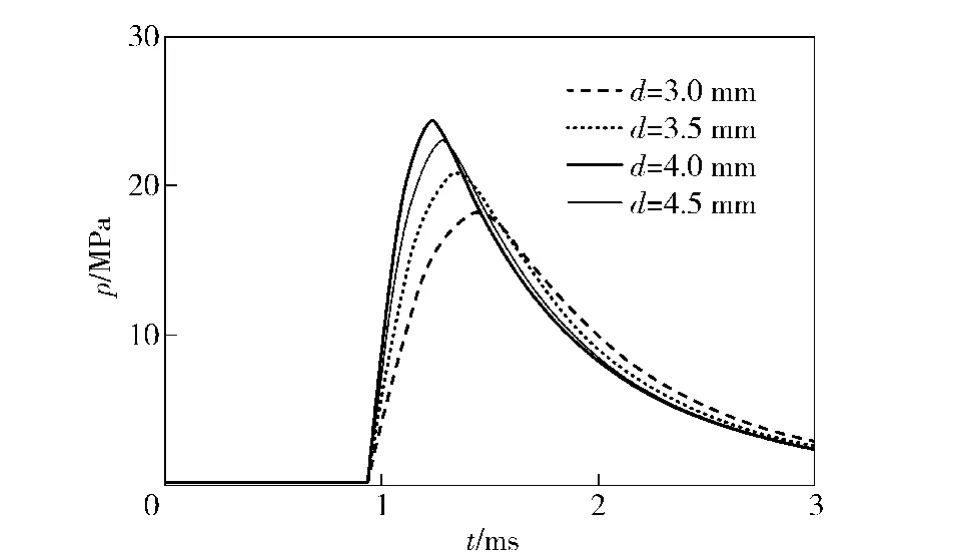
Fig.11 Influence of clearance on gas chamber pressure

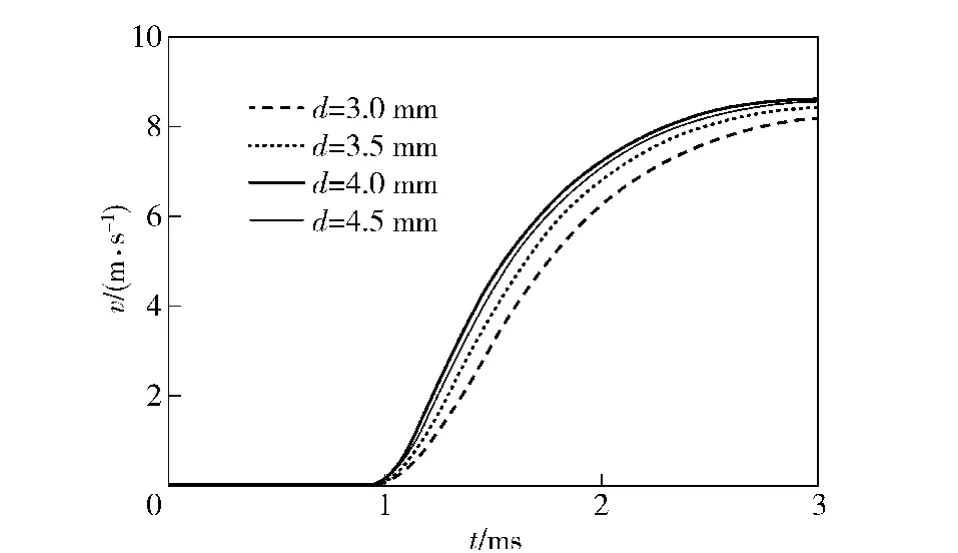
Fig.12 Influence of clearance on automatic mechanism speed

3 Conclusions

1)Analyzed the variable-mass thermodynamic processes of gas-operated automatic weapon，a variable-mass thermodynamics calculation model coupling the interior ballistics and gas-operated device is established and verified.

2)The bore pressure and bullet velocity are solved by using the model，and the trend of bore pressure is analyzed.It shows that the coupling factor should be considered in the calculation of the internal ballistics and dynamics of gas chamber accurately.

3)The established model can be used to solve the influences of the structural parameters on the gas chamber pressure and the velocity of automatic mechanism.

4)The model can also be used to quantitatively analyze the change of flow flux at the gas-guiding hole.

［1］GAN Gao-cai.Dynamics of automatic weapon［M］.Beijing:Weapon Industry Press，1990:26 － 33.(in Chinese)

［2］LU Jia-peng.Gas dynamics of automatic weapon［M］.Beijing:Weapon Industry Press，1988:456－464.(in Chinese)

［3］LIAO Zhen-qiang，WANG Tao，YUE Shi-hai.The calculation method of gas dynamics of weapon［M］.Beijing:Weapon Industry Press，1988:221－228.(in Chinese)

［4］NI Zhi-jun，ZHOU Ke-dong，HE Lei.Consistency research of interior ballistic performances of the metal storm weapon system with side powder chambers［J］.Acta Armamentarii，2005，9(5):595－599.(in Chinese)

［5］HAN Xiao-ming，BO Yu-cheng，WANG Hui-yuan，et al.Optimal design of gas-guiding device structure parameter in internally-powered gatling weapon system［J］.Journal of Gun Launch＆ Control，2008，(2):50－53.(in Chinese)

［6］WANG Wan-qing.Analysis on dynamics and optimization of model M60 general purpose machine gun of the 7.62 mm caliber［D］.Nanjing:Nanjing University of Science and Technology，2007.(in Chinese)

［7］Compile Group of Infantry Automatic Weapon and Design of Ammunition.Manual of infantry automatic weapon and design of ammunition［M］.Beijing:National Defense Industry Press，1977:39－84.(in Chinese)