钛酸锶钡陶瓷的铁电极化疲劳效应*

刘俊刁，陈如麒，沈 韩，陈 敏，姚李兵

(1.惠州学院电子科学系, 广东 惠州516007;2.华南农业大学公共基础课实验教学中心, 广东 广州 510642;3.中山大学物理科学与工程技术学院, 广东 广州 510275)

铁电材料由于具有多种特殊的性质，在电子、信息等许多领域得到广泛应用。其中，非挥发性铁电寄存器是其重要的应用之一[1]。但铁电材料固有的极化疲劳效应，严重影响了其商业化进程[2]。饱和极化强度Psat、剩余极化强度Pr、矫顽场Ec是描述铁电体极化的几个重要参数，通常采用Sawyer-Tower(简称ST)电路测量铁电体的电滞回线，由回线可读出上述参数。导致疲劳的因素很多，如畴壁钉扎[3]、界面复制[4]、氧空位迁移[5]、空间电荷等[6]，但宏观都表现为极化强度随反转次数的增加而逐渐减小。

由于ST电路采用了积分电容，故样品的线性和非线性漏电电流、线性和非线性非铁电电容等信号都会被电容积分而难以区分，对测量结果造成较大影响，难以得到纯铁电机构的信号。在铁电屏蔽理论基础上发展起来的微分电滞回线谱分析方法可较好地解决这一问题[7-10]。测量电路如图1(a)所示，不采用积分电容，直接测量流过样品的电流I随样品两端电压U的变化，有

(1)

其中A为样品电极面积，l为样品厚度，D为电位移，Q=AD为样品表面的电荷，E=U/l为样品内的电场。Q(U)曲线与电滞回线D(E)有相同的形状，只差一个比例系数。若在三角波作用下，(dU/dt)为常数，则I(U)与电滞回线微分形式(dD/dE)曲线形状一致，只差一个比例系数。与电滞回线D(E)相对应，称I(U)为微分电滞回线，可用有限个高斯函数精确拟合[9-10]。目前最常使用的循环伏安特性分析方法和铁电开关峰分析方法与微分电滞回线谱类似[11-12]，都是在三角波作用下测量样品的IV曲线，但前两种方法未分出信号中非铁电成分的影响，也没有将电流峰用高斯函数拟合并用高斯参数来表征材料的铁电性能。由于三角波峰值点左右两边电压的斜率不相等，电压不连续，使得微分电流在峰值电压附近出现跳变，对结果的分析带来一定的难度。本文拟将该方法改进为采用正弦电压，并用新方法研究钛酸锶钡陶瓷的极化疲劳效应，以验证该方法的有效性和可靠性。

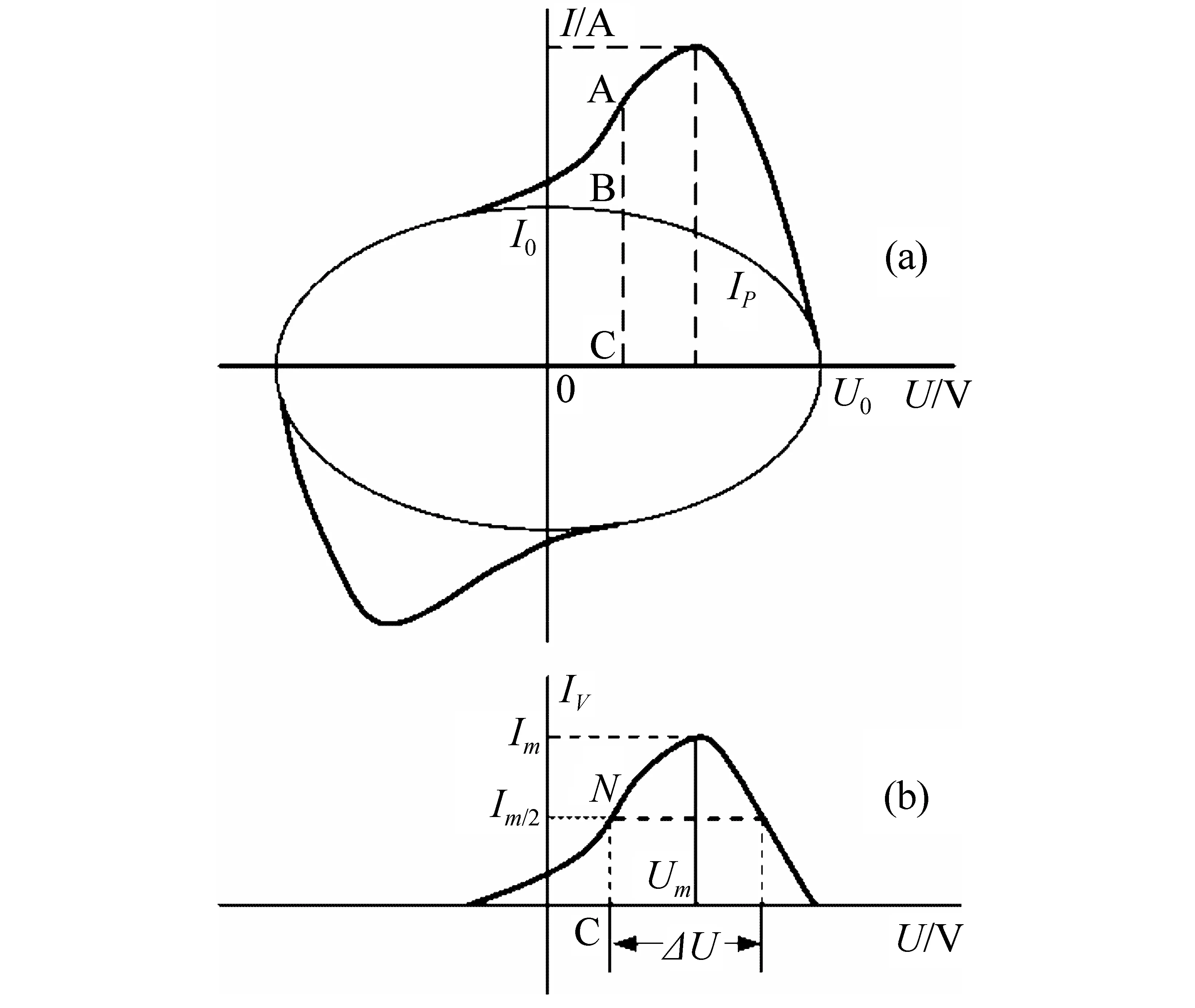
图1 正弦波作用下的微分电滞回线基本成分

1 基于正弦波的微分电滞回线

测量电路仍采用图1(a)，外加电压为圆频率为ω，峰值为Up的正弦波U=Upsinωt，通过样品的电流I用精度为1 pA，等效输入电阻约为1 kΩ的微电流计测量。I由3部分组成[13]，

I=IR+IP+IF

(2)

其中，IR为样品漏电电阻R提供的传导电流，IP为样品的非铁电电容CP所提供的电流，IF为样品纯铁电电容CF提供的电流。上述3种电流的理想I(U)曲线分别示于图1(b至d)。时间t增大时，电容的I(U)曲线按顺时针方向扫描。实验得到的I(U)曲线应该是图1(b至d)多个成分的组合。凭以上各成分的特征，很容易从总I(U)曲线中将每个分量定量分离出来，从而得到纯铁电性的贡献。由于正弦波在U=±Up处有dU/dt=0，故此两点处I(U)曲线是连续的，没有跳变。但此时(dU/dt)不为常数，由式(1)可知I(U)与(dD/dE)的形状略有不同。

2 钛酸锶钡陶瓷微分回线解谱方法

实验样品为Ba0.95Sr0.05TiO3(BST)陶瓷圆片，室温时为铁电相。样品厚l=0.22 mm，一面烧Ag电极，另一面溅射Au电极做成电容器，电极面积A=3.14 mm2。在样品两面加上图2套图形式的正弦电压。由于BST样品的直流电阻R>108Ω，用HP4192A阻抗分析仪测出其50 Hz时的电容CH约为0.400 nF，相应地，样品容抗为|1/ωCH|=7.96×106Ω<

I(t)=IP(t)+IF(t)

(3)

将电压加在样品两端电极上经过10倍周期时间后，样品慢慢进入了稳定的循环，用数字存储示波器记录微分回线示于图2，其微分回线是单峰的。设极化反转次数为N，持续工作时间为t1。f=50 Hz时，样品每秒极化反转100次，每小时反转7 200次，连续观测至少100 d。

图2 BST陶瓷样品的微分回线

在正弦波作用下，图1(c)所示由非铁电性线性电容引起的电流IP很容易根据电容的容抗(1/jωCP)写出

(4)

根据式(4)，可计算并画出图3(a)所示的IP(U)椭圆。椭圆的第二、第三象限部分与所测的微分回线几乎重合。根据式(3)，在总电流中扣除IP(U)就可得到图3(b)所示的纯铁电性的电流IF(U)。图3(a)中I<0的部分可采用相同的方法处理。由于所测BST陶瓷样品的微分回线具有中心对称性，故只需分析I>0的部分，否则两部分需分开讨论。IF(U)微分回线的峰高Im、峰位Um和半高半宽ΔU随极化反转次数N的变化关系就可用来表征样品铁电极化疲劳的特性，称(N,Im,Um,ΔU)为疲劳参数。将图3(b)曲线积分，可得到电滞回线Q(U)，其矫顽电压Uc与微分回线的Um接近。

图3 BST陶瓷微分回线解谱方法

3 钛酸锶钡陶瓷的极化疲劳

取Up=400 V，f=50 Hz，测得样品微分回线的ΔU(N)和Im(N)曲线示于图4。图中只画出了N>105的曲线，在N<105时，ΔU较小，Im较大，呈现较尖锐的IF(U)峰，且ΔU和Im的数值几乎不变，样品未出现明显的疲劳。随着N继续增大，样品的ΔU与Im单调变化。N>105后，样品开始出现疲劳的现象。根据图4，可将疲劳过程大致分成3个阶段。第1阶段为N=105-3×106，已开始出现疲劳的征兆，但ΔU和Im变化很小，微分回线的形状变化不明显，只是样品的正常老化过程起主要作用。第2阶段出现在N=3×106-2×108，该阶段ΔU迅速变大，Im迅速变小，微分回线越来越扁平，相应地，传统电滞回线所围面积逐渐变小，极化强度逐渐变小，样品出现明显的疲劳效应。第3阶段为N>2×108，该阶段Im减小到一定程度后就保持几乎不变，但ΔU仍继续增大至大于所加正弦电压的峰值400 V，此时，图3(b)所示的IF(U)曲线有很大一部分已延伸到U<0的一端，说明热运动就足以将样品某一表面上的铁电电荷激发到另一面，使得样品的极化强度值很小。样品严重疲劳，已不能使用。

图4 BST陶瓷疲劳参数随反转次数的变化

疲劳过程中Im持续变小，可解释为样品中的荷电缺陷和铁电电荷在交流电压作用下向样品的表面迁移，到达样品电极附近对电畴产生钉扎作用而不能继续移动。钉扎效应已被公认为疲劳的主要原因之一[3]。而在同成分的薄膜中，由于钉扎效应不明显，反转了108次后仍未观察到疲劳[14]。

4 结 论

将微分电滞回线的测量信号由三角波改为正弦波之后，测量方法和解谱方法都更为简便。与传统使用极化强度来表征疲劳效应相比，新方法采用(N,Im,Um,ΔU)等系列参数，表征更为全面。该方法可将BST陶瓷的极化疲劳清晰地划分为3个阶段，有望推广应用于单晶、薄膜等其它铁电样品，发展成为一种描述极化疲劳效应的有力手段。

参考文献：

[1]RAMESH R, AGGARWAL S, AUCIELLO O.Science and technology of ferroelectric films and heterostructures for non-volatile ferroelectric memories[J].Materials Science and Engineering, 2001，32: 191-236.

[2]TAGANTSEV A K, STOLICHNOV I, COLLA E L, et al.Polarization Fatigue in Ferroelectric Films[J].J Appl Phys, 2001，90(3): 1387-1420.

[3]GRUVERMAN A, RODRIGUEZ B J, NEMANICH R J, et al.Nanoscale observation of photoinduced domain pinning and investigation of imprint behavior in ferroelectric thin films[J].Journal of Applied Physics, 2002，92(5): 2734-2739.

[4]GROSSMANN M, LOHSE O, BOLTEN D, et al.Lifetime estimation due to imprint failure in ferroelectric SrBi2Ta2O9 thin films[J].Applied Physics Letters, 2000，76(3): 363-365.

[5]LI KWOK TUNG, LO V C.Simulation of oxygen vacancy induced phenomena in ferroelectric thin films[J].J Appl Phys, 2005，97(034107): 1-8.

[6]OKATAN M B, MANTESE J V, ALPAY S P.Effect of space charge on the polarization hysteresis characteristics of monolithic and compositionally graded ferroelectrics[J].Acta Materialia, 2010，58: 39-48.

[7]李景德, 李智强, 陆夏莲, 等.铁电屏蔽理论[J].物理学报, 2000，49(01): 160-163.

[8]丘翠环, 陈丽,李智强.铁电和铁磁微分回线谱分析[J].广东工业大学学报, 2002，19(2): 69-72.

[9]沈韩, 陈敏, 朱贵文, 等.铁电极化疲劳效应的微分电滞回线谱分析[J].四川大学学报：自然科学版, 2005,42(S2): 73-76.

[10]朱贵文, 周伟华, 沈韩, 等.铁电体的极化疲劳和历史记忆效应[J].中山大学学报：自然科学版, 2005，44(4): 40-44.

[11]YU JUN, DONG XIAOMING, ZHOU WENLI,et al.Study on the I-V characteristics of ferroelectric thin film systems with the structure of MFSM[J].Materials Science and Engineering B, 2000，76: 22-25.

[12]ZHU G D, LUO X Y, ZHANG J H, et al.Imprint effect in ferroelectric poly(vinylidene fluoride-trifluoroethylene) thin films[J].Journal of Applied Physics, 2009，106(7):074113.

[13]李景德, 沈韩,陈敏.电介质理论[M].北京: 科学出版社，2003.

[14]PONTES F M, LONGO E, LEITE E R, et al.Study of the dielectric and ferroelectric properties of chemically processed BaxSr1-xTiO3 thin films[J].Thin Solid Films, 2001,386(1): 91-98.