分形插值在地球化学数据中的应用*

张 焱，成秋明，周永章，谢淑云，，刘小龙，徐德义

(1. 中山大学地球科学系,广东 广州 510275;2.中国地质大学(武汉)地质过程与矿产资源国家重点实验室；3. 中山大学地质过程与矿产资源探查广东省重点实验室，广东 广州510275;4.中国地质大学(武汉)地球科学学院,湖北 武汉 430074)

1985-1991年期间，很多外国学者先后对分形插值做了研究应用[1-6]，同时一些国内学者做了进一步研究[7-14]，得到改进的分形插值方法，在此基础上对岩石断裂面进行了研究并取得了较好的效果，但对分形插值在地球化学数据中的应用效果一直缺乏清晰的阐述。本文对西藏驱龙地区的实际数据以及正态分布数据、分形分布数据进行反距离加权法、克里格法和分形法三种插值方法计算，并对比分析它们的应用效果。

1 数据来源

1)服从正态分布的数据：使用随机数产生方法在数学软件MATLAB[15]中产生。产生数据后将它存入文本。

2)服从多重分形分布的数据：基于De Wijs模型产生的数据[16-17]，De Wijs模型数据的构造过程与multiplicative cascade processes相同。Multiplicative cascade processes可产生典型的多重分形。这种过程可由生成元矩阵基于规则网格用Kronecke连续乘积构造出来[18]。

3)西藏驱龙地区Ag含量的实例数据。该研究区位于西藏自治区墨竹工卡县甲马乡境内，此矿区是当前中国地质勘查界重点关注的矿区，更是冈底斯多金属成矿带东段中正在进行勘探的最重要铜矿区，与拉萨相距110 km[20]，驱龙矿床产于拉萨地体南缘火山-岩浆带中。

2 插值方法

2.1 分形插值

分形插值函数与初等函数的主要差别在于前者具有的分形特征，如它有非整的分数维数，它是针对集合而非针对点的[21]。文中使用的分形插值曲面方法依据迭代函数系统构造。就目前而言，迭代函数系统中的变换多用于仿射变换，而当处理任意四边形不规则剖分情形时仿射迭代函数系统无法实现，故文中采用射影变换来解决这一难题。

有关射影变换下分形插值曲面的实现及模型建立步骤算法参见文献[12,19]，随后在软件MATLAB6.5中编程实现即可得到所需模型。

2.2 反距离加权法

反距离加权插值法是空间确定性插值中的一种，它是基于相近相似的原理,以插值点与样本点间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大[20]。

反距离加权插值中幂指数的选择对插值结果有很大影响，通常其幂指数默认为2，但实际应用中幂指数的选择要视研究区的具体情况而定，通常情况下，在插值点稀少或是数据缺乏的区域，适当提高幂指数可以提高模型的精度[22]。

2.3 克里格插值

克里格方法的适用范围为区域化变量存在空间相关性，其实质是利用区域化变量的原始数据和变异函数的结构特点，对未知样点进行线性无偏、最优估计[23]。

应用克里格方法插值的主要步骤为：

1) 将数据导入软件ArcGIS中，然后对数据进行分析，看它是否服从正态分布，如果服从正态分布，接着看它是否存在主导趋势，如果存在则选用泛克里格法；如果不服从正态分布，则选取某种变换如对数变换使其服从正态分布；

2) 根据数据选择适合的方法，此处针对选用哪种克里格方法，如普通克里格、简单克里格等；

3) 接着计算样点间的距离矩阵、样点间的属性方差等，设置好建模的相关参数如块金值、基台值、变程、拟合函数等，这些参数在设置时必须严格控制，因为一旦参数改变对结果的影响都很大；

4) 绘制方差变异云图、经验半变异函数图、拟合理论半变异函数图等，最后对插值结果进行预测。

2.4 数据检验标准

抽取源数据中的一部分数据作为训练样本，其余数据作为检验样本，在ArcGIS软件中应用地统计分析模块对数据进行交叉检验。对比3种插值方法总的流程详见文献[19]。

3 结果与讨论

3.1 正态分布数据插值结果图

各种插值方法结果图1。由图可知3种插值方法得出的结果无明显区别。

3.2 多重分形分布数据插值结果图

各种插值方法结果见图2。分析各种插值方法与原始数据的偏差，由偏差结果得出分形插值结果与原始值更接近的结论。

3.3 实例分析-西藏驱龙Ag元素

以西藏驱龙Ag含量[24]作为应用实例展示分形插值方法的应用效果。将Ag含量分布图的整个区域(图3)分成4部分。首先选取最右下角的区域作为研究区一，该研究区为整个区域内含异常值较高的区域，对此研究区进行3种插值方法比较。

针对此组Ag含量分布数据，进行各种插值方法之前，详细分析了使用克里格方法插值时各种参数对插值结果的影响情况；经过反复调试，此处运用反距离加权插值时所选幂指数为2；运用分形插值时垂直比例因子的选取经过反复验证此处垂直比例因子取0.3时效果最佳。

然后从偏差角度、平均偏差值角度、参数角度分别分析各种插值得出的结果的区别，具体步骤参见文献[19]。

最后在ArcGIS中生成插值结果图。对于此组实例数据采用比值对插值结果进一步分析。

1)分别计算IDW插值方法、Kriging插值方法和分形插值方法的偏差结果。

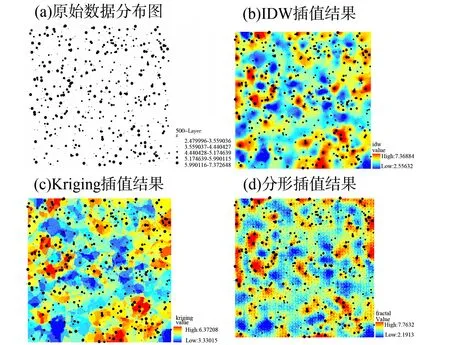
图1 原始数据图与插值结果图

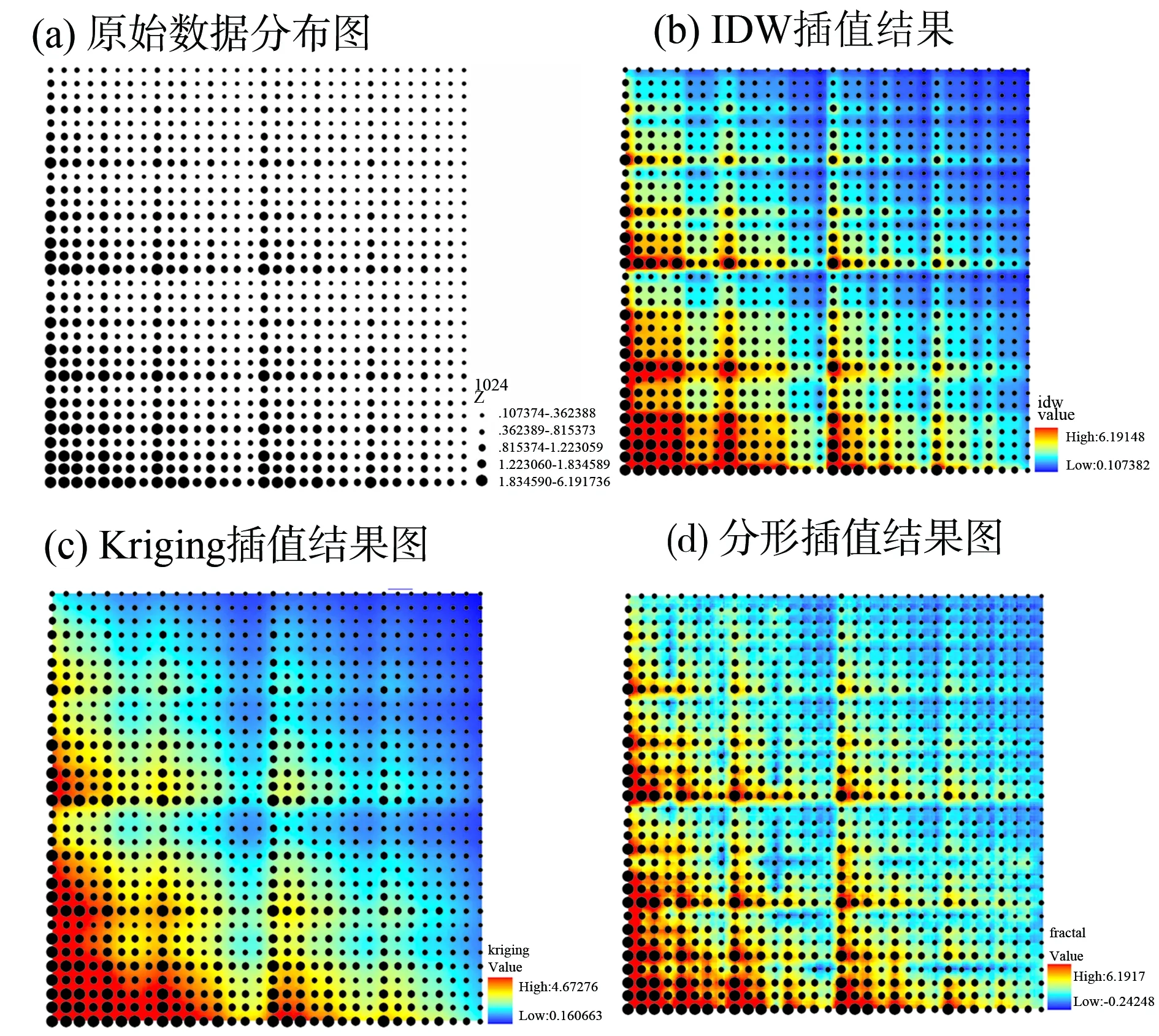
图2 原始数据图与插值结果图

2)根据偏差结果可以统计出各个偏差百分比范围内IDW、Kriging、分形3种插值方法所占的个数，从统计个数可看出3种插值方法的优劣。

从统计结果得出偏差百分比在(0～10%)范围内时由分形插值得出的结果最佳，总体上分形插值结果较其他两种插值方法偏差小，一个点除外，分析其原因，此点是该区域浓度最高点，也即异常点，此点误差偏大可能是多种原因造成的，可能与该区域地质背景有关，也可能与分形插值本身算法也有关。

3) 从平均偏差值角度分析。使用公式(1/n)∑(xi-x)2(其中x为原始值，xi为插值后得出的预测值，n=20)计算出各种插值方法的平均偏差。

图3 原始数据图与插值结果图

通过计算得出Kriging插值后的平均偏差为0.001 24，IDW插值后的平均偏差为0.001 22，分形插值后的平均偏差为0.002 51，得出Kriging插值结果的平均偏差与IDW的很接近，而由分形插值得出的平均偏差确比另外两种插值方法的要高，其原因是检验点中浓度最高点造成的，从而影响了整体的平均偏差。该点称为异常点，属局部异常，针对此区域Ag含量来说，局部奇异性反映的是Ag元素在地质过程中的富集和贫化规律，通过分形插值方法可以突出其奇异性信息。

4)从参数角度分析。从参数对照表(见表1)中各参数可以看出：由分形插值得出的平均值、最小值、最大值、标准差、方差与原始值最接近。整体趋势上看，由分形插值得出的结果与原始数据更接近，说明针对此组实际地球化学数据，使用分形插值方法更能够突出其异常值。

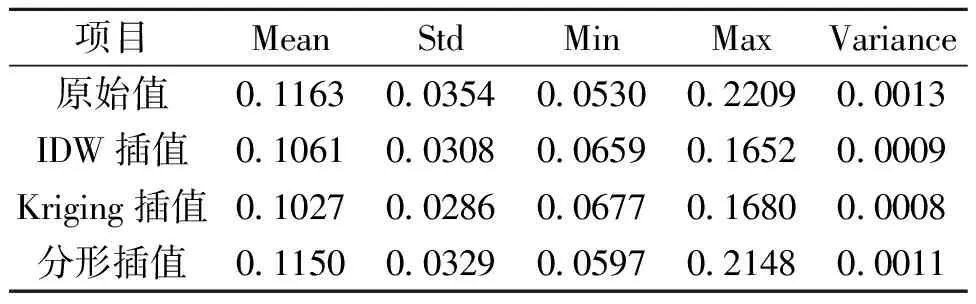
表1 参数对照表

5)插值结果图见图3所示。从插值结果图中可以看出异常区域存在于Ag含量高浓度区域，而且从图中还可以看出使用反距离加权插值法后数据趋于平滑，而克里格和分形插值后数据趋于粗糙，高浓度区域使用分形插值后浓度相对偏高，低浓度区域使用分形插值后浓度相对偏低。

为了对比分形插值方法与普通克里格、反距离加权插值方法的结果，将分形插值方法结果与其他两种插值方法结果作比值(图4)。

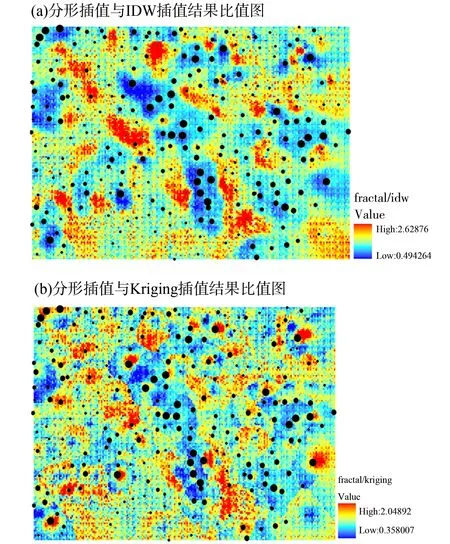
图4 比值结果图

因IDW插值根据空间数据的距离远近赋权重，效果上插值后造成数据平滑；克里格插值中的变异函数的正确选择可以保证其插值结果的精度，但是对于局部具有奇异性的地球化学数据，变异函数不能够完全反映。从图5中分形插值与IDW插值和克里格插值结果比值可以看出比值高的地段为那些具有奇异性的地段，分形插值结果与克里格插值结果、反距离加权插值结果比值越高，说明运用分形插值得出的结果能够突出其异常区域，越有利于增强矿化富集地段的信息，而对于具有奇异性的地球化学场来说，传统的统计方法是不大适合的，因为它们对少数的奇异数据所反映的局部异常不是很敏感。因为此区域相对整个Ag含量区域属于高背景区，异常相对集中，规模较大，异常强度高，所以使用分形插值能够突出其局部异常。

研究区二为西藏驱龙Ag含量区域右上角的子区域，对此组数据使用方法如前所述，在此不再累述。插值结果图见图5。

该研究区属于整个Ag含量低浓度区，异常相对较少，强度较低，但用分形插值法仍能够体现其局部异常，此组数据局部异常较前组数据弱。

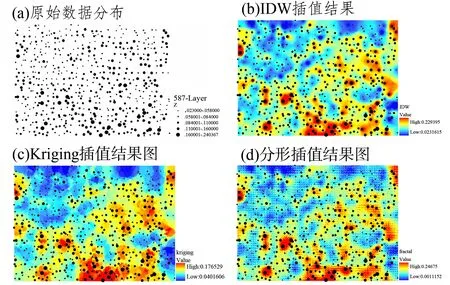
图5 原始数据图与插值结果图

图6 比值结果图

为对比分形插值方法与普通克里格、反距离加权插值方法的结果，将分形插值方法结果与其他两种插值方法结果作比值(图6)。由图6可知，发现分形插值与克里格、反距离加权插值的比值明显低于前组，造成这种差别的原因在于此组数据中Ag含量浓度总体上低于前组。从比值图中可知分形插值法的确适合具有异常值的地球化学数据，因此研究区属于整个Ag含量低浓度区，异常相对较少，强度较低，但使用分形插值法仍能够体现其局部异常，只是此组数据局部异常较前组数据效果甚微。

4 结 论

1) 服从分形分布的数据使用分形插值的效果比反距离加权和克里格法的效果好；

2) 服从正态分布的数据，三种插值方法效果相差不大；

3) 具有奇异性的数据，使用分形插值得出的效果较其他两种插值方法好。

本研究结果可供地质工作者在实际工作中选取合适插值方法时借鉴。本文的插值效果比较方法也可以为科学工作者参考。

致谢：感谢石家庄经济学院张生元教授、中国地质大学(武汉)陈志军博士在数据处理、论文修改等方面提供的宝贵意见。感谢中山大学王建华教授对定稿提出的宝贵建议。

参考文献：

[1] VOSS R F. Random fractal forgeries[M]∥Earnshaw R A,ed. Fundamental Algrithms in Computer Graphics.Berlin : Springer-Verlag, 1985:805-835

[2] BARNSLEY M F, DEMKO S G. Iterated function systems and the global construction of fractals[C]∥Proc of the Royal Soc, London, A399,1986:243-275.

[3] HEWETT T A. Fractal distribution of reservoir heterogeneity and their influence on fluid transport [C]. SPE 15386, 1986.

[4] MATHEWS J L. Fractal methods improved Mitsue miscible predictions[C]. SPE18327 , 1989.

[5] DALLA L, BOUBOULIS P. Hidden variable vector valued fractal interpolation functions [J]. Fractals, 2005, 13(3): 227-232.

[6] BARTON C C, SCHOLZ C H. The fractal size and spatial distribution of hydrocarbon accumulations[M]∥Fractal in Petroleum Geology and Earth Processes.New York:Plenum Press,1995:13-34.

[7] 姚东良. GIS中类地球化学勘探数据的分形插值模型与图示化[D]. 广州：广州地球化学研究所, 1998 .

[8] 谢和平, 孙洪泉. 分形插值曲面理论及其应用[J]. 应用数学和力学. 1998, 19(4):297-306.

[9] 孙洪泉, 谢和平. 分形插值曲面及其维数估计[J]. 中国矿业大学学报,1998, 27(2):217-220.

[10] 李红达,叶正麟,王小平. 分形插值曲面[J]. 计算机辅助设计与图形学学报,2002, 14(4):316-319.

[11] 孙明岩.分形插值的全息方法与局息方法 [D]. 长春: 东北师范大学, 2003.

[12] 赵瑞,叶正麟. 平面任意四边形剖分上的射影分形插值曲面[J]. 计算机工程与应用,2006, 34(3):26-28.

[13] WILLIAMS H, TURNER S, KELLEY S, et al. Age and composition of dikes in southern tibet:new constraints on the timing of east-west extension ANS lt's relationship to post-collisional volcanism[J]. Geology, 2001, 29(2): 339-342.

[14] 孙洪泉,谢和平. 岩石断裂表面的分形模拟[J]. 岩土力学，2008, 29(2):347-351.

[15] 李海涛,邓樱．MATLAB程序设计教程[M]．北京：高等教育出版社，2002．

[16] 陈志军. 多重分形局部奇异性分析方法及其在矿产资源信息提取中的应用[D]. 武汉：中国地质大学, 2007 .

[17] MANDELBROT B B. The fractal geometry of nature[M]. San Francisw: W H Freemanand Company, 1982.

[18] EVERTSZ C J G, MANDELBROT B B. Multifractal measures[M]∥Peitgen H O,et al, eds. Chaos and Fractals. New York: Springer-Verlag, 1992:922-953.

[19] 张焱.分形插值在地球化学数据中的应用效果研究[D].武汉：中国地质大学, 2009.

[20] 杨少平，张华，刘应汉，等．西藏驱龙铜矿区及其外围找矿前景地球化学评价[J]．地质学报，2006, 80(10)：1558-1565．

[21] 李水根，吴纪桃．分形与小波[M]．北京：科学出版社，2002．

[22] 王勇，李朝奎，陈良，等．权重对空间插值方法的影响分析[J]．湖南科技大学学报:自然科学版，2008, 23(4)：77-80．

[23] 汤国安，杨昕．ArcGIS地理信息系统空间分析实验教程[M]．北京：科学出版社，2006．

[24] XIE Shuyun, CHENG Qiuming, KE Xianzhong, et al. Identification of geochemical anomaly by multifractal analysis[J]. Journal of China University of Geosciences, 2008, 19(4): 334-342.