具有脉冲投放益虫生物控制害虫的捕食-食饵模型*
程惠东
(山东科技大学理学院,山东 青岛 266510)
在自然界生物系统中,有关害虫的科学有效的治理一直是人们研究的问题,人们试图利用喷洒杀虫剂作为控制害虫的数量,这会造成环境污染,也对天敌益虫及人类造成伤害,经常会因为害虫的变异及适应性的增强而使得杀虫剂失效,这样显然不利于人们的长远发展,也不经济;而利用人工培养或从外地迁入天敌的方法,即定期进行天敌投放,以达到控制害虫的目的,这样可以避免环境污染给人类带来的损失。因此很多学者对生物控制进行了大量的研究与讨论[1-8],这些研究大多是在彻底根除害虫的情况下,而引入大量的天敌[4-8],但是从生态平衡和经济方面考虑,根除害虫是不太可能,也不科学的;我们希望天敌最小的投放量,最长的投放周期,使害虫种群与益虫种群持续生存,故本文致力于害虫生物治理的研究。
1 模型及预备知识
许多作者对捕食-食饵系统的研究已做了很多工作并且得到了很好的结果[2-5]。近年来,阶段结构模型也越来越受到关注,许多文献对阶段结构单种群模型进行数学分析[6-9],最近,Weng等[9]考虑了下面的捕食- 食饵模型
其中,x(t),y1(t),y2(t)分别表示食饵、幼年和成年捕食者种群的密度,其具体的生物学意义可参见文献[9],但是这个模型没有考虑到捕食者幼体的成长期和功能反应情况。
由于害虫的出生率、死亡率等生存指数几乎总是与年龄、种群的大小或发展阶段有关,幼虫大多生活的庇护所里,我们进行的管理策略几乎不起作用,我们还注意到,幼年不具有生育能力,从幼年到成年的成熟期作为一个常数时滞。由此害虫的阶段结构、时滞以及人类周期性的干扰等生物现象是经常发生的。近几年脉冲微分方程在生物模型中的应用正在兴起[5-9],而且时滞微分方程在生物模型中也有广泛的应用[10-11],但是脉冲时滞微分方程在种群动力学上的应用不太常见中,由此,我们引入如下具有阶段结构脉冲时滞的HollingII功能反应的捕食模型
(1)
这里xj(t),x(t)分别表示幼年、成年害虫种群的密度,r>0成年害虫的出生率,γ>0,c>0分别表示幼年、成年害虫种群的死亡率,τ时期从出生到长成成年的时间,re-γτx(t-τ)表示幼年害虫在t-τ时刻的出生数(即rx(t-τ))到t时刻除去死亡以后的剩余数,表示幼年到成年的转化数;u>0表示天敌的释放量,d>0表示天敌的死亡率,β>0表示天敌的捕食率,λ>0表示被捕食的食饵向捕食者的转化率,α>0反映的是同种群生物之间相互干扰的大小程度[8-9]。y(nT+)=limt→nT+y(t),y(nT)=limt→nT-y(t),x(t),xj(t)对t>0都是连续的,具体细节请参阅文献[9-10]。
因为幼虫不具有危害性或者危害性较小,并且不具有出生率,所以控制害虫主要是指对成虫的控制。注意到系统(1)的第二第三个方程中不显含变量xj(t),因此只需研究下面系统(1)的子系统
(2)
从生物意义出发,只在区域D={(x,y)|x,y>0}上考虑系统(2)的动力学行为,于是系统(2)满足初始条件
(φ1(s),φ2(s))∈C+=
(3)
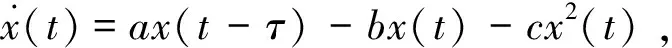
(i)若a 假设害虫(食饵)从捕食系统中完全消失,即害虫根除,须有x(t)=0,t>0。在此条件下,我们表明与周期脉冲投放天地同步,天敌(捕食者)种群出现相同周期的震荡。 在害虫根除的条件下,首先要了解天敌(捕食者)在nT (5) 在任何两次脉冲时间间隔内对微分方程(5)进行积分求得 y(t)=y(nT)e-d(t-nT),nT 这里y(nT)是天敌在nT时刻的初始值,对于系统(5)第二个方程。依据离散动力系统的频闪映射得 y((n+1)T)=y(nT)e-dT+u=f(y(nT)) (6) 于是有 系统(5)有唯一的一个全局渐进稳定的正周期解。 因为系统(5)的解是 y*(t),t∈(nT,(n+1)T] 于是有下面的引理。 引理3[5]系统(5)有唯一的一个全局渐进稳定的正周期解y*(t),即系统(2)有唯一的一个在t∈(nT,(n+1)T]上的“害虫根除” 周期解(0,y*(t)),并且对系统(2)的任何解(x(t),y(t)),都有当limt→∞y(t)=y*(t)。 记 定理1 如果u≥u*或者T≤T*,则系统(2)“害虫根除” 周期解(0,y*(t))是全局吸引的。 (7) 成立。由系统(2)的第三个方程可知, 从而 因此,对上述ε>0,存在一个正整数n1,使对t≥n1T时,都有 (8) 由(8)式及系统(2)的第一个方程,对t≥n1T+τ,有 (9) (10) 的唯一全局渐进稳定的正周期解。由(10)式知,对t∈(nT,(n+1)T],有 根据脉冲微分方程的比较定理,对任意ε1>0,存在n3>n2,当t>n3T+τ,都有 (11) (12) 因此,当t→∞时,有 (13) 注:定理1表明了较短的脉冲周期(T),或者对天地进行较大的脉冲释放量(u),是害虫根除周期解全局吸引的充分条件,这也说明了这些参数对系统动力学行为有重要影响。 定理1表明了较短的脉冲周期(T),或者对天敌进行较大的脉冲释放量(u),是害虫种群最终完全根除,事实上,从生态平衡及经济方面考虑,种群最终完全被根除是困难的,也是不科学的。因此我们希望让害虫与天敌在共存的条件下,控制在经济危害水平(EIL)E之下,从而不会带来严重的经济损失。由此我们给出有效且符合实际的害虫控制策略。 记 定理2 如果u** 因而由系统(2)的第一个方程,对t≥n1T+τ,有 (14) 考虑比较方程 (15) 本文根据现实的生物意义,把脉冲、时滞和阶段结构捕食模型中,一方面得到害虫彻底根除的充分条件,另一方面得到了能够把害虫控制在作物经济危害水平(EIL)之下,这在阶段结构种群动力学上还不多见。这与许多作者大多得到的彻底根除害虫的条件和结论是不同的。事实上,在现实生活中彻底根除害虫是很难实现的,也是不科学的。因此我们给出了不必彻底根除害虫的充分条件,即当天地的最小投放量u**与最小投放周期T**时,害虫处于作物经济危害水平(EIL)之下。从生态平衡、种群的多样性及经济方面考虑,这样的害虫控制策略更具现实意义。从数学上看,我们还获得了定理的条件及模型的动力学行为依赖于时滞τ的结论,这说明这个时滞为“有害”时滞。 参考文献: [1] AIELLO W G, FREEDMAN H I. A time-delay model of single-species growth with stage structure [J]. Math Biosci, 1990, 101:139-153. [2] MENG X, JIAO J, CHEN L. Nonlinear analysis: The dynamics of an age predator-prey model with disturbing pulse and time delays [J]. Real World Applications, 2008, 9(2): 547-561. [3] 程惠东,孟新桂,王芳.一类时滞非自治Lotka-Volterra扩散生态系统的全局吸引性[J].中山大学学报:自然科学版,2008,47(2):18-22. [4] 程惠东.脉冲投放益虫化学控制害虫管理模型[J].中山大学学报:自然科学版,2010,49(3):8-11. [5] MENG X, CHEN L. A stage-structured si eco-epidemiological model with time delay and impulsive controlling [J]. Journal of Systems Science and Complexity, 2008: 427-440. [6] GOURLEY S A, KUANG Y. A stage structured predator-prey model and its dependence on through-stage delay and death rate [J]. J Math Biol, 2004, 49:188-200 . [7] NIETO J J, RODRIGUEZ - LOPEZ R. Periodic boundary value problems for non-Lipschitzian impulsive functional differential equations [J]. J Math Anal Appl, 2006, 31 (8): 593-610. [8] HASTINGS A. Global stability in two species system [J]. J Math Biol, 1978, 5: 399-403. [9] WANG W, CHEN L. A predator - prey system with stage structure for predator [J]. Comput Math Appl, 1997, 33 (8): 83-91. [10 ] J IAO J J, PANG G P, CHEN L S, et al. A delayed stage-structured predator prey model with impulsive stocking on prey and continuous harvesting on predator [J]. Applied Mathematics and Computation, 2008, 195(1): 316-325. [11] MENG X Z, CHEN L S. Almost periodic solution of non-autonomous Lotka-Volterra predator-prey dispersal system with delays [J]. Journal of Theoretical Biology, 2006, 243:562-574.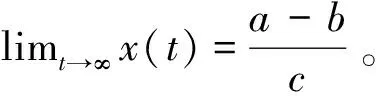

2 “害虫根除”周期解的全局吸引性
2.1 “根除害虫”周期解的存在性
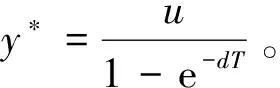
2.2 “害虫根除”周期解的全局吸引性
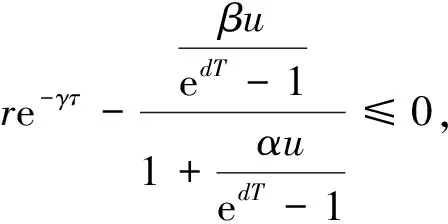
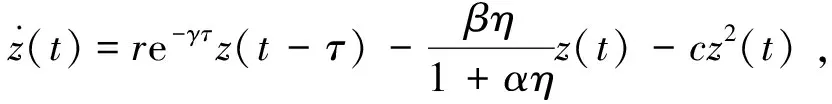
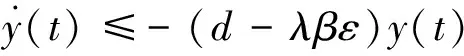
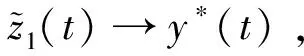

3 害虫的控制策略
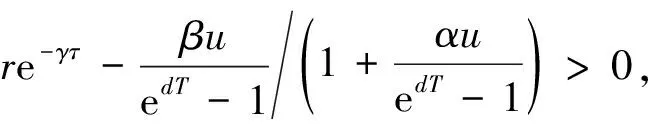
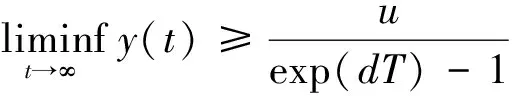
4 生物意义

