空心圆柱滚子轴承接触力学数值仿真
张洪伟, 陈家庆,张向东
(北京石油化工学院 机械工程学院,北京 102617)
圆柱滚子轴承广泛应用于航空航天、铁路、船运、汽车、冶金矿山和其他行业的各种机械中,随着技术的不断进步,对轴承的承载能力和使用性能的要求越来越高。研究表明,普通的直素线滚子轴承在受载后滚动体两端不可避免会产生边界应力集中现象,即所谓“边界效应”。为了克服这种边缘效应,人们进行了大量研究[1-9]。
由于空心圆柱滚子轴承可以更好地适应振动冲击性载荷,改善轴承系统的润滑冷却条件,人们已经尝试将无预载荷的空心圆柱滚子轴承应用于一些低速、重载场合,并在结构设计、理论和应用推广研究上做了很多工作[6,8,10]。与普通圆柱滚子轴承相比,空心圆柱滚子轴承接触区的状态发生了比较明显的变化,而且其接触状况与空心度及载荷大小有关[11]。对于空心圆柱滚子接触力学的研究具有重要的理论意义,国内、外许多学者开展了大量富有成效的工作[2-3,6-7]。由于接触问题复杂,求解困难,对空心圆柱滚子轴承的研究仍有许多问题亟待解决,特别是该轴承在滚子两端是否仍存在边界应力集中现象,不同空心度下滚子轴承接触状态的变化规律如何,迫切需要进一步深入研究。
数值模拟技术因其经济性和高效性成为研究复杂接触力学问题强有力的手段,许多学者利用数值仿真技术进行了圆柱滚子轴承的相关研究[6-8],但仍有许多关键技术有待解决和深化。下文基于有限元法,对不同空心度下圆柱滚子轴承的接触状态进行了数值模拟,对接触应力及等效应力分布进行了分析,为空心圆柱滚子轴承的实际应用提供理论依据。
1 仿真模型建立
空心度是空心滚子的重要参数,其定义为
K=d1/d2,
式中:d1,d2分别是空心滚子的内、外径。
以轴承系统中最大承载滚子与内圈滚道的接触为分析对象,取直素线空心圆柱滚子体内的空心孔洞为单一圆柱状。几何尺寸及载荷为[6]:圆柱滚子外半径R1=5.5 mm,接触有效长度L=21 mm,内滚道直径F=49.50 mm;滚子和套圈采用相同材料,弹性模量为206 GPa,泊松比为0.3。该最大承载滚子在正常工作时所承受的外载荷F0=14 113 N;取滚子与滚道之间的摩擦系数为0.2,忽略润滑剂的影响。
考虑到圆柱滚子轴承在结构和载荷方面的对称性,取1/4圆柱滚子和1/8内圈(包括轴颈)实体建立有限元分析模型,单元类型选用8节点六面体单元。为提高计算效率,考虑到滚子与套圈相互接触引起的应力效果主要在滚子和套圈接触宽度附近,而接触半宽很小,因此,在接触线附近的单元网格分得非常细密。由于要研究滚子边缘效应,所以沿接触轴线方向网格非常细密,其他较疏。建立的实心滚子及空心滚子有限元模型,分别如图1、图2所示。

图1 实心圆柱滚子有限元模型图
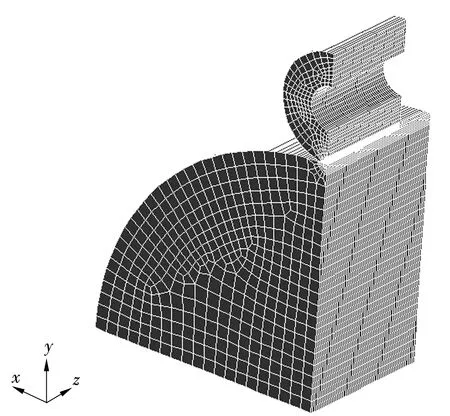
图2 空心圆柱滚子有限元模型图
模型边界条件为:在各个对称面上施加对称边界条件,y=0底平面施加y方向约束;z=0中间横截面施加z方向约束;x=0对称面施加x方向约束。载荷施加于滚子上部轴线上,沿y轴负方向。
接触问题是最困难的非线性问题之一,利用MSC.MARC选择基于直接约束的接触算法。该方法对接触描述的精度高,且有普遍适应性,不需要增加特殊的界面单元,也不涉及复杂的接触条件变化。
2 不同空心度下有限元数值模拟
基于建立的有限元模型和边界条件,对不同载荷作用下,滚子空心度为0%,20%,30%,40%,50%,60%,65%,70%,80%下的直素线圆柱滚子接触状态进行了有限元分析。
2.1 不同空心度下等效应力分析
由于等效应力是影响轴承疲劳寿命的主要因素,所以,以轴承危险区域的等效应力来进行空心度的分析评价。分析结果表明,重载(F0=14 113 N)作用下不同空心度对于等效应力有较大影响。
如图3所示,在受载前滚子与内圈的接触线是AB线。计算结果表明,滚子内、外壁线上的应力大于中间部分应力,外壁线AB上的应力又大于内壁线CD上的值。在所计算的空心度范围内,最大等效应力都是发生在滚子与内圈接触线AB附近。

图3 空心滚子有限元模型图
图4为重载(F0=14 113 N)下等效应力沿AB线的分布规律。横坐标原点为中间截面上的A点,右端则是滚子端部上的B点。由图4可见,实心滚子与空心滚子的接触应力沿滚子轴向的分布规律基本相似,都是在滚子的中部应力分布均匀,端部应力明显变大,出现边界应力集中。

图4 等效应力沿滚子轴向分布(F0=14 113 N)
图5为重载(F0=14 113 N)下滚子轴向方向最大等效应力随空心度的变化规律。由图5可知,随着空心度的增加,最大等效应力先是减小,然后再增大。此变化过程中有一个转折点存在,大约位于空心度65%左右,此时,等效应力降低率最大。随后,随空心度的增大,等效应力值开始增加,且大于实心滚子对应的等效应力。所以基于等效应力考虑,重载作用下合理空心度可选择为65%。

图5 沿滚子轴向最大等效应力随空心度的变化规律
图6为轻载(F0=4 kN)作用不同空心度情况下,滚子等效应力沿滚子轴向方向分布规律。与重载作用下相比,等效应力变化规律相似,总的来说,相比实心滚子,空心度小于80%时,轴向等效应力分布规律及数值变化不大,在边界存在应力集中现象;但当空心度为80%时,等效应力明显增大。有限元分析表明,不同空心度的滚子在不同的载荷作用下,等效应力的危险区域相同,都是在滚子与套圈接触线附近。
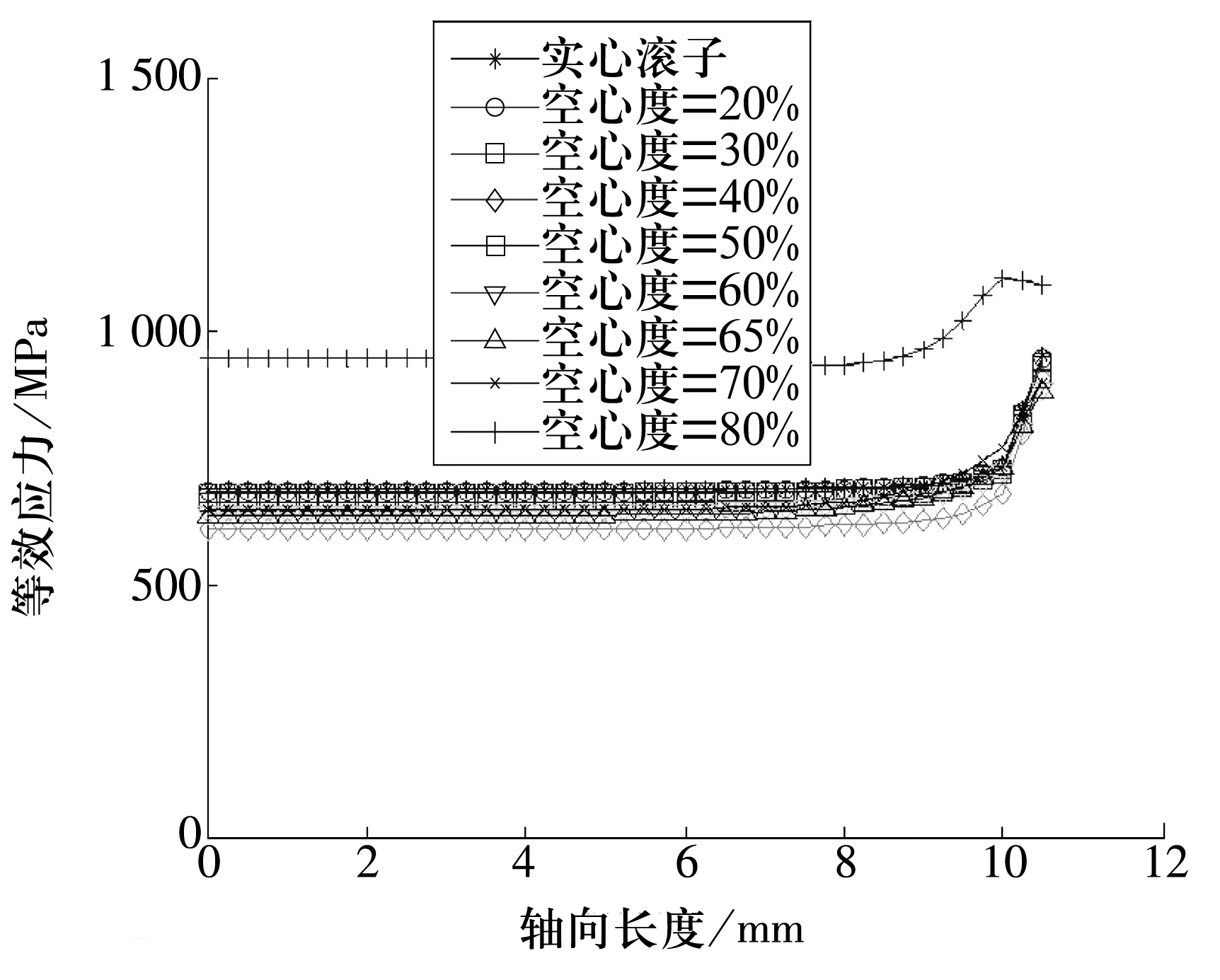
图6 等效应力沿滚子轴向分布(F0=4 kN)
2.2 不同空心度下接触应力分析
图7为重载(F0=14 113 N)下不同空心度的接触应力分布曲线。从图中可以发现,接触应力沿滚子轴向的分布规律不同于等效应力。
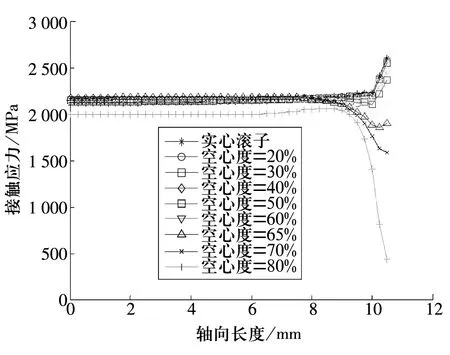
图7 接触应力沿轴向分布规律(F0=14 113 N)
总体来说,在空心度小于60%时,在滚子边缘处仍存在明显应力集中现象,而且在空心度小于80%时,中部接触应力差别不大;但端部的接触应力随空心度的增大逐渐减小。当空心度为60%时,边界应力已小于滚子中部的应力,即接触应力已不存在边缘效应。此后,随着空心度的进一步增加,滚子中部的接触应力也随着增大,而边界应力进一步减小,使中部的应力远大于边界点的应力。当空心度达到80%时,相比实心滚子,中部应力及边界应力均显著减小。
过大的空心度,将严重削弱滚子整体刚度,会引起较大的变形或局部皱折,如空心度为80%时,径向压缩量达到了0.5 mm,不能满足刚度要求。因此,在重载作用下,基于接触应力合理分布的角度来看,即减小边缘效应,同时沿轴向尽可能分布均匀,空心度约为60%时较为合理,此时径向压缩量为0.081 3 mm。在工程重载应用中,综合考虑等效应力和接触应力,并避免过大的径向压缩量,滚子最佳空心度可取为60%左右。
对于轻载(F0=4 kN)时不同空心度的接触应力,如图8所示。与重载分析结果类似,接触应力沿滚子轴向分布与等效应力分布不同,几何边缘处应力随空心度的增加,逐渐降低,当空心度大于60%时,端部接触应力小于中部接触应力,不存在边缘效应。
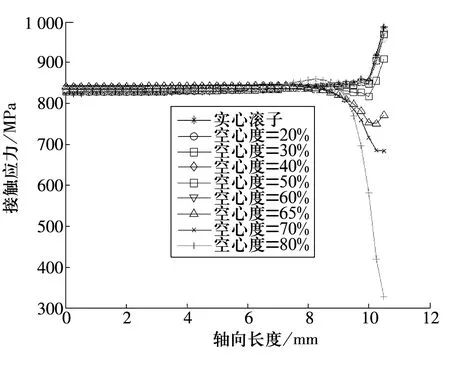
图8 接触应力沿轴向分布规律(F0=4 kN)
当空心度为70%时,相比实心滚子等效应力和接触应力均有减小,而且沿轴线分布较均匀,接触应力没有边缘效应,此时,径向压缩量为0.048 7 mm。所以在轻载作用时,综合各种因素,合理空心度可选择为70%。
2.3 沿接触宽度方向等效应力分析
计算结果表明,沿接触宽度方向,不同空心度下的最大等效应力都发生了不同程度的偏离,即最大等效应力值并不位于初始接触对称线中心,而是向一侧发生了偏移,具有不对称特征。图9为重载作用下空心度60%时,沿接触宽度方向的等效应力分布。可以看出,最大等效应力并不是位于接触中心,而是略偏于中心位置,这种接触区域的等效应力不对称分布与摩擦有关。
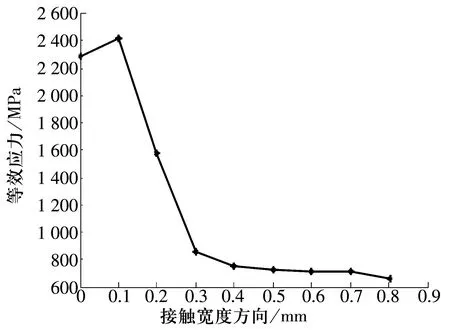
图9 空心度60%沿接触宽度方向等效应力分布
2.4 不同载荷对于接触状态的影响
图10为空心度60%时不同载荷作用下沿滚子轴向的等效应力分布。从图10可以发现,随载荷变化,等效应力分布规律相似,均存在明显的边界效应。在载荷较小时(小于10 kN),应力变化范围较小;当载荷大于10 kN时,应力增加较为明显,应力值的变化和载荷没有必然的线性规律。

图10 不同载荷下等效应力沿滚子轴向分布
图11为空心度60%时不同载荷下接触应力沿滚子轴向的分布。从图11可知,随着载荷的变化,沿滚子轴线方向接触应力变化较为明显,但分布规律相似,而且均不存在显著边界效应,载荷越大,边界应力减小越大。

图11 不同载荷下接触应力沿滚子轴向分布
2.5 不同空心度下滚子内壁应力分析
图12为不同空心度的等效应力云图。从图12可以看出,滚子内壁的等效应力随着空心度的增大而增大。空心度较小时,等效应力较大区域集中在滚子与滚道接触线附近,随着空心度的增加,滚子内壁处的等效应力随之增大。而且最大等效应力的具体位置随空心度变化也发生变化。
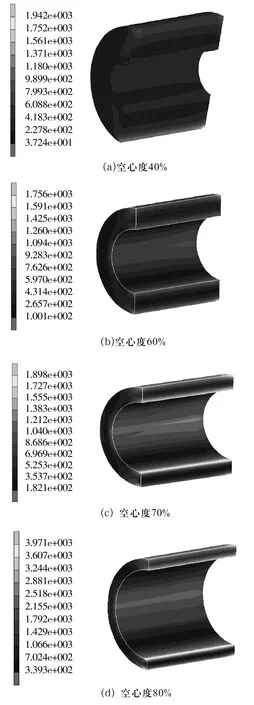
图12 不同空心度下滚子等效应力云图
图13为空心度65%和空心度80%时滚子沿径向的等效应力分布,即图3中AC方向。可以看出,当空心度为65%时,滚子内壁上的等效应力值已接近滚子与滚道接触线附近的应力值。随着空心度增加,内壁等效应力值继续增加。当空心度达到80%时,内壁等效应力值已远超过接触区域应力值,所以在空心度较大时,等效应力最大值出现转移现象,应关注滚子内壁的等效应力分布。
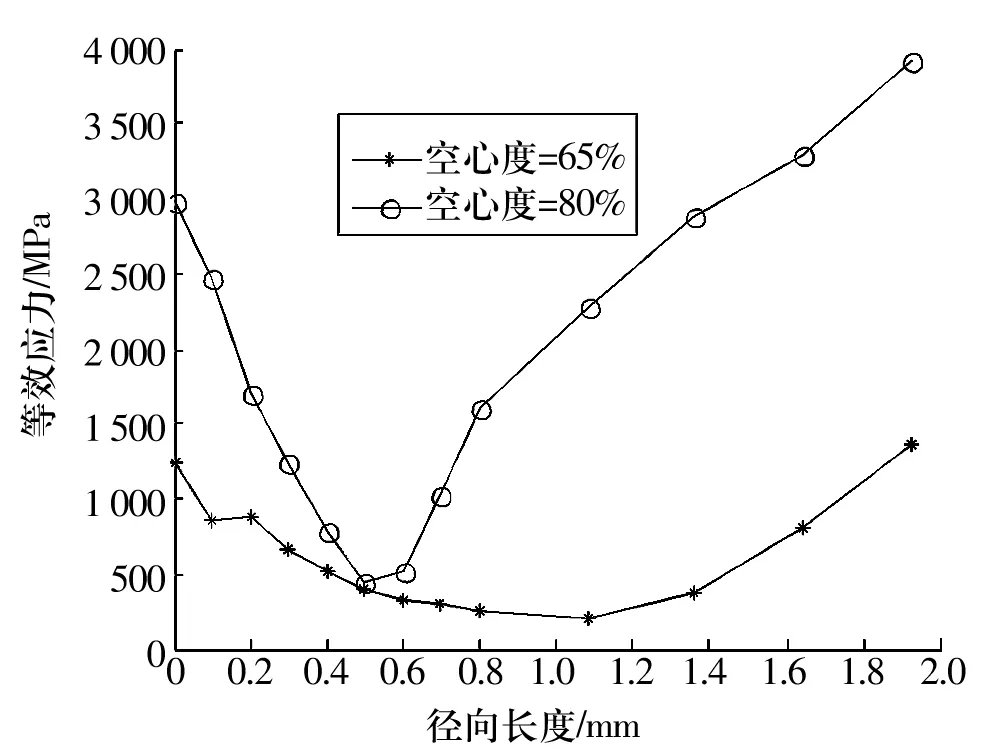
图13 不同空心度时沿径向等效应力分布
弯曲应力是评价空心圆柱滚子轴承的一个重要附加原则。研究表明,滚子内壁的弯曲应力较大时,可能会诱发弯曲疲劳[12]。图14为空心度60%时滚子内壁沿周向(图3中沿AE环向)的弯曲应力分布。从图14可以看出,在承载情况下,滚子每滚动一周,内壁上任一点的弯曲正应力变化规律为:从最大拉伸应力逐渐减小,并反向转变成压缩应力,逐渐增加到最大压缩应力值,然后再逐渐变化到最大拉应力值。这与文献[10]中的理论研究结果是相似的。

图14 空心度60%时滚子内壁周向弯曲应力分布
当空心滚子承载过大,弯曲应力值超过疲劳极限时,经过一定应力循环次数后,则可能引起弯曲疲劳。所以在进行空心度优化设计时,还应考虑弯曲应力的影响。
3 结论
(1) 空心度对等效应力及接触应力的影响规律是不同的,合理的空心度可减小接触应力的边缘效应,但等效应力滚子两端的边界应力集中总是存在的。
(2)在相同空心度下,圆柱滚子轴承的等效应力和接触应力随载荷的变化规律是不同的。在轻载作用时(小于10 kN)等效应力随载荷变化较小;而载荷大于10 kN时,等效应力随载荷变化明显。接触应力随载荷变化比较明显。
(3)载荷不同时,最佳空心度的理论值不同,应针对不同载荷工况,综合考虑等效应力、接触应力,并满足滚子的刚度要求,将空心度限定在一定范围内来进行空心度的优化设计。
(4)空心滚子内壁的等效应力值随空心度的增大而增大,最大等效应力的具体位置随空心度变化而沿壁厚方向有转移现象。在空心度较大时(文中为65%),滚子内壁的等效应力会超过外壁的等效应力值,成为危险区域。在空心滚子的设计中同时应考虑弯曲应力的影响,避免滚子内壁发生弯曲疲劳断裂。

