红外热像检测的3D建模与1D建模的对比

刘颖韬,郭兴旺,郭广平

(1.北京航空材料研究院,北京 100095;2.北京航空航天大学机械工程及自动化学院,北京 100083)

红外热像无损检测技术由于检测速度快、无污染和非接触,在复合材料制件的无损检测中应用越来越广泛。对红外热像无损检测进行建模分析,可以确定表面温度信号与制件几何参数、材料热物性参数、缺陷几何参数、缺陷热物性参数、边界条件和检测中的加热方式等因素的关系,有助于设计最佳的热激励方式及确定信号的最佳采集时段,有助于开发新的检测方法和数据处理方法。从而优化检测条件,包括热激励条件、数据采集时段和数据处理方法等。

在红外热像检测的建模分析方面,虽然国内外学者做了大量深入的研究,不仅对典型的一维模型、二维模型和三维模型进行了仿真研究[1-2],而且还进行了复杂模型的研究,如两个缺陷位置重叠的建模分析[3]、针对裂纹缺陷的建模分析[4]、用于地雷探测的复杂模型分析[5]、裂纹特征的建模[6]、混凝土缺陷的建模[7]、激励强度对检测的影响[8]和空腔自然对流对红外检测的影响[9]等。但是为了便于缺陷分析和定量评价,三维模型常常被简化为一维模型,从而忽略横向导热的存在,这样将引入误差。这种误差在什么情况下会带来怎样的影响,目前研究较少。它的影响依据所研究的内容有所不同,主要是影响对缺陷大小和埋深进行估算的准确性。笔者将通过建模对比分析,对模型简化引入的误差进行定量研究。

1 典型的三维模型和简化后的一维模型

红外热像无损检测中常使用三维模型进行建模分析。典型的三维模型有用于模拟分层缺陷的三维模型和用于模拟金属腐蚀缺陷的三维模型(见图1和2)。

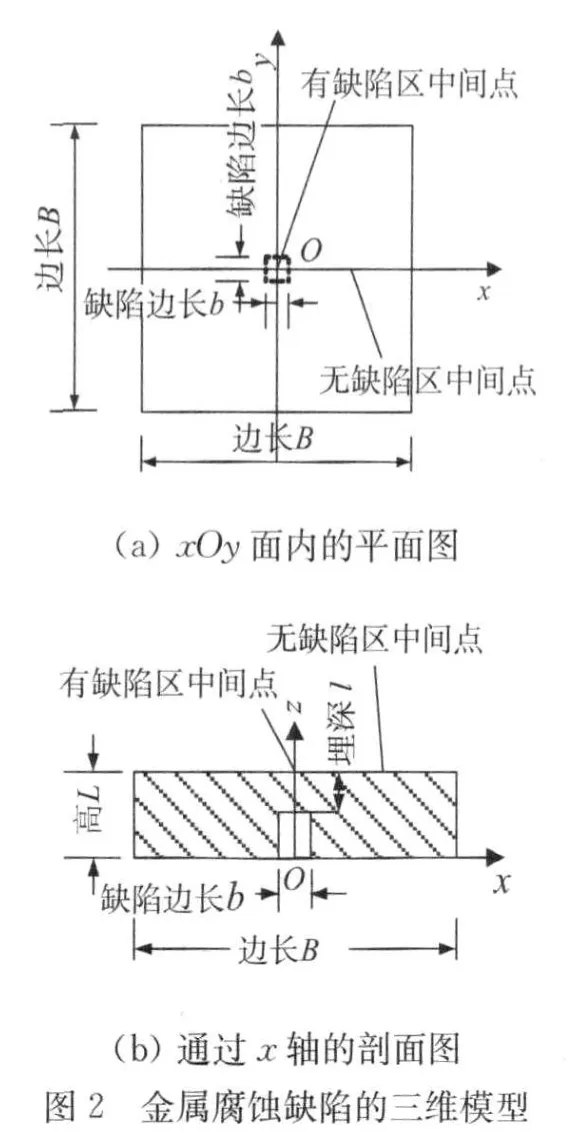
图1(a)中的阴影区域为分层缺陷,L为试件厚度,l为缺陷深度,d为缺陷厚度,R为模型半径,rd为缺陷半径,q为加热的热流密度。图1(b)中无缺陷区简化为一层有限厚度板,厚度为试件厚度L。有缺陷区为三层结构的有限厚度板,中间层为缺陷,厚度为d。

图2中B为试件的边长,b为缺陷区的边长,L为试件厚度,l为缺陷深度,加热面在z=L处。该模型简化为：无缺陷区为一层有限厚度板,板厚为试件厚度L,有缺陷区同样为一层有限厚度板,板厚为缺陷深度l。

以下使用有限单元法进行数值求解,采用有限元分析软件ANSYS实现。

2 三维模型和一维模型计算结果的比较

2.1 分层缺陷

首先考察表面温度的空间分布。计算模型为图1中的三维模型,加热阶段不考虑向环境散热,冷却阶段边界条件为对流换热,初始温度同环境温度,本底材料为碳纤维增强塑料(CFRP),缺陷为空气,热物性参数见表 1,计算参数为试件厚度L=0.002 m,缺陷厚度d=0.000 1 m,缺陷深度l=0.000 9 m,试件半径R=0.05 m,缺陷半径rd=0.005 m,热流密度q0=1.0×106W/m2,脉冲宽度τh=0.01 s,计算截止时间τstop=5 s,网格大小Siz=0.000 02 m。

表1 材料的热物性参数

图3给出在时刻τ=1.872 8 s时表面温度的空间分布和表面温度对径向r的偏微分曲线。可见,由于缺陷为空气,其导热性差,导致缺陷区的表面温度明显高于无缺陷区的表面温度,并且表面温度对径向r的偏微分在缺陷边缘附近取得最大值。由于横向传导的热流密度qr与横向温度梯度∂θ/∂r成正比,因此这种横向温度梯度的存在必然导致横向导热的发生。一维模型完全忽略了横向导热的存在,其解与三维模型的解有本质的区别。

先以图1中的模型为对象进行对比。设加热方式为矩形窄脉冲,脉冲宽度为 τh,本底材料为CFRP,缺陷为空气,模型参数及计算参数同上。三维模型边界条件为：上表面在加热后绝热,加热过程中忽略对流和辐射换热,其余表面始终绝热。

三维模型中选取的比较点为有缺陷区和无缺陷区的中间点,回避了横向导热明显的区域——缺陷边界。如果在这两个点的温度变化上出现偏差,则更能说明横向导热的影响。

在比较之前,首先定义绝对差和相对差,绝对差定义为：

相对差定义为：

这里θ1为一维模型下的计算温度值,θ2为三维模型下的计算温度值的插值。这是由于两个计算结果的计算时间点不同,不能直接进行比较,所以在比较之前对二维模型下的计算温度值进行了线性插值。比较结果见表2。

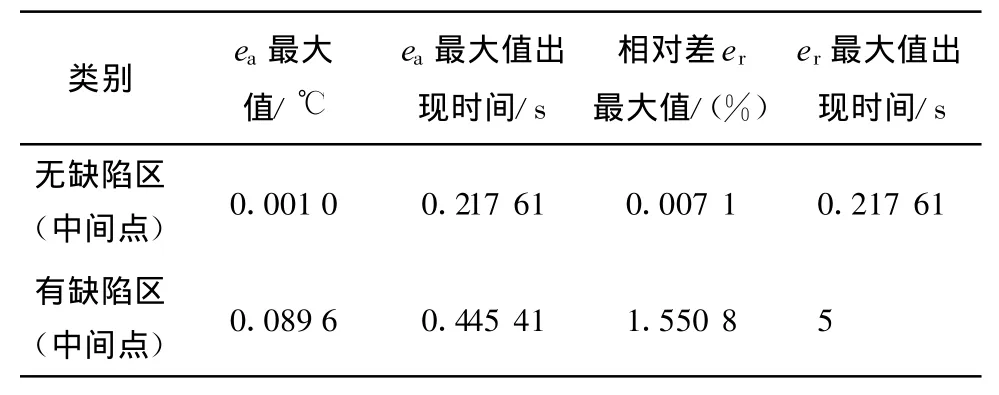
表2 柱状三维模型与一维模型表面温度的比较结果

由表2可以看出,有缺陷区中间点的温度出现了比较明显的偏差(1.550 8%),而无缺陷区中间点的温度几乎没有偏差(0.007 1%),这是因为有缺陷区很小,其中间点距离缺陷边缘——温度梯度较大的区域很近,而无缺陷区较大,其中间点距离缺陷边缘较远,两者受横向导热的影响程度不同。

2.2 金属腐蚀缺陷

金属腐蚀缺陷的基体材料为铝,热物性参数见表1,计算参数为试件的边长B=0.02 m,试件厚度L=0.002 m,缺陷区的边长b=0.002 m,缺陷深度l=0.000 6 m,热流密度q0=1.0×106W ◦m-2,脉冲宽度τh=0.01 s,计算截止时间 τstop=0.5 s,网格大小Siz=0.000 2 m。边界条件为：上表面在加热后绝热,加热过程中忽略对流和辐射换热,其余表面始终绝热。三维模型选取的比较点为有缺陷区的中间点和无缺陷区的中间点,比较结果见表3。

表3 金属腐蚀缺陷三维模型与一维模型比较的过余温度

表3中无缺陷区中间点在两种模型下的温度极为接近,而有缺陷区中间点的温度有明显不同,受横向导热的影响非常严重。综合表2和表3可以看到,金属腐蚀缺陷三维模型中的横向导热比分层缺陷三维模型中的更为明显,主要是因为前者基体材料是铝,后者基体材料是CFRP,铝的热扩散率远远高于CFRP的热扩散率,热量能够更快地向四周扩散。也就是说,当其它条件都相同时,不计材料导热的各向异性,热扩散率越高的材料中横向导热越明显,由模型简化带来的误差越大,一维模型的理论解应用于三维问题得到的结果越不准确。

通过试验发现,即使是对于热扩散率很低的复合材料,随着时间的延长,横向导热的影响也会变得很明显。图4为带人工脱粘缺陷的蜂窝板样件的红外热像检测结果,右边为脱粘区。从图中可见,由于横向导热的存在,脱粘区的边界发生了“移动”。

3 结语

当其它条件相同时,不计材料导热的各向异性,热扩散率越高的材料中横向导热越明显,由三维模型简化为一维模型进行分析所带来的误差越大,一维模型的理论解应用于三维问题得到的结果越不准确。即使是对于热扩散率很低的复合材料,随着时间的延长,横向导热的影响也会变得很明显,从而影响利用一维模型所得到的结论的正确性及分析的准确性。对于经历较短的检测时间或对于精度要求不高的定量分析,可以使用简化后的一维模型,但是对于更加复杂的检测过程或精度要求较高的定量分析,需要谨慎地使用简化的一维模型,并在使用前利用三维和一维模型进行仿真分析,评估模型简化带来的误差。

[1]Galietti U,Ladisa S,Pappalettere C,et al.Hybrid procedure to charac terize hidden defects in composite[J].Thermosense XXIV SPIE,2002(4710)：599-609.

[2]V ladimir P Vavilov.A ccuracy of thermal NDE numerical simulation and reference signal evolutions[J].Thermosense-XXISPIE,1999(3700)：14-19.

[3]V ladimir P Vavilov.Three-dimensional analysis of transient thermal NDT p roblems by data simulation and p rocessing[J].Thermosense XXII SPIE,2000(4020)：152-163.

[4]Robin Steinberger,Thomas G rünberger,Pau l O'Leary.Simulations and analyticalmodels for optimization of photothermal surface crack detection[J].Thermosense XXIIISPIE,2001(4360)：524-533.

[5]Vladimir P Vavilov,Douglas Burleigh,A lexey G K limov.Advanced modeling of thermal NDT p rob lems：from buried landmines to defects in composites[J].Thermosense XX IV,SPIE,2002(4710)：507-521.

[6]李大鹏,张利群,赵岩松.红外无损检测中的裂纹特征提取和图形重建方法研究[J].计算机测量与控制,2005,13(7)：624-626.

[7]黄红梅,魏臻.红外无损检测的三维有限元仿真[J].安徽工业大学学报,2006,23(3)：313-314.

[8]李国华,赵会友,朱红秀,等.红外热像检测的数值优化[J].煤矿机械 ,2004(9)：23-24.

[9]范春利,孙丰瑞,杨立.缺陷表面温度分布及空腔自然对流对红外检测的影响[J].激光与红外,2005,35(7)：504-507.

[10]Sergio Marinetti,Alberto Muscio,Paolo Giu lio Bison,et al.Modeling of thermal non-destructive evaluation techniques for composite materials[J].Thermosense XX II Bellingham,SPIE,2000(4020)：164-173.

[11]Bison P G,Bressan C,Cavaccini G,et al.NDE of compositematerials by Thermalmethod and Shearography[J].Proc SPIE Thermosense-XIX.Bellingham：SPIE,1997(3056)：220-229.

[12]杨世铭,陶文铨.传热学[M].北京：高等教育出版社,1998：420-424.