在线逆向拍卖供应商投标决策支持模型

呼大永，冯玉强，付 铭，曲云波

(1.哈尔滨工业大学经济与管理学院，150001哈尔滨，superhudayong@163.com;2.哈尔滨工业美术设计学校，150059哈尔滨)

在线逆向拍卖供应商投标决策支持模型

呼大永1，冯玉强1，付 铭1，曲云波2

(1.哈尔滨工业大学经济与管理学院，150001哈尔滨，superhudayong@163.com;2.哈尔滨工业美术设计学校，150059哈尔滨)

为了解决基于分包算法的在线逆向组合多属性拍卖中供应商决策支持问题，通过对供应商投标行为的分析，以供应商收益最大化为目标，提出了基于计量经济学分包算法的分包确定模型以及供应商投标策略模型.通过算例演示表明，该方法可以有效地提高供应商的收益、降低拍卖过程中信息不对称所带来的负面影响.

逆向拍卖;组合多数性拍卖;决策支持;投标策略模型

随着世界经济的发展及互联网和信息技术的广泛应用，近几年针对在线逆向拍卖(也称“采购拍卖”)的研究成为学界的研究热点之一［1－4］.然而，在实际应用中在线逆向拍卖技术也存在一定问题:1)由于逆向拍卖属于组合多属性拍卖研究范畴，因此其胜者确定问题(Winner Determination Problem，WDP)为 NP 问题［5］，无法在多项式时间内给出可行解［6］;2)供应商的投标存在不均衡性.对利润高的商品投标较多，对利润低的商品常常没有供应商投标;3)单一商品采购无法形成规模效益，因此无法有效降低成本.目前，在实际应用中采购方通常采用将采购商品划分成若干标段的方式(也称分包方法［7－11］)来解决上述问题.其中，国内学者呼大永等［10］以商品“相似性”度量以及供应商“竞争性”度量作为拆分包标准，利用科学计量学方法及供应商偏好信息设计了基于先验信息的拆分包算法，并通过利用2009年我国某省药品采购招标数据对所述方法进行了验证，结果表明该方法不但能够降低WDP算法的复杂度，而且可以有效地降低采购成本，均衡供应商竞争性.

尽管分包算法在一定程度上解决了采购拍卖胜者确定中存在的部分问题，保证了作为拍卖发起者的采购方的利益.然而从采购拍卖长远发展以及系统完整性考虑出发，仅提供采购方和第三方的决策支持是远远不够的，作为采购拍卖不可或缺的参与主体——“供应商”的利益同样应当得到保护.

当前，针对在线拍卖特点的投标策略模型研究还比较少，大多以目前电子商务中应用最广泛的英式拍卖为背景［12］.2009 年，Bertsimas等［13］针对单物品和多物品的情况分别建立了在线拍卖最优投标策略模型，并给出了在线拍卖投标决策支持模型应满足的3个约束条件:1)依据网上拍卖的重要特征提供决策，应满足在线拍卖对实时性、安全性以及供应商数量及类型的要求;2)决策提供的算法在实际操作中具有可用性和实践性，即能在多项式时间内给出可行解;3)决策算法中所用到的参数可以通过先验数据或经验信息获得.通过采用eBay网站上1 772条拍卖数据进行验证，结果表明该模型可以有效地为投标行为提供快速、可靠的决策支持.

本文基于文献［13］的设计理念，在文献［10］所述的基于计量经济学的分包算法的基础上，通过对供应商投标行为的分析，设计了供应商决策支持决策模型，并通过算例分析了算法的有效性.

1 网上采购拍卖供应商投标行为分析

若想建立供应商投标决策支持模型，首先应考虑分包算法以及采购机制的特点;其次，若泛泛地将所有供应商按一种模式进行决策支持，势必会降低支持效率，因此还应该知道各类供应商的投标策略及其偏好特点.由于科学计量学分包算法与采购机制均已经确定，因此本文仅对供应商投标行为进行分析，针对投标行为对供应商进行分类，为供应商投标决策支持提供依据.

与正向拍卖相似，在采购拍卖中供应商对于增加获胜的可能性与增加获胜后可能获得的利益之间存在偏好问题，即供应商存在风险态度问题［14］.依据供应商的风险策略类型描述如下:

1)风险厌恶.这类供应商偏好降低不能中标的风险几率，因此宁愿降低自己在中标后所获得的利益以提高中标概率.因此，在这类供应商的投标策略中应该尽量提高投标的“质量”(价格属性和非价格属性)，进而提高供应商中标几率.然而尽管投标的“质量”有所提高但其中标后的所得利润在此3类决策支持中是最小的.各类供应商风险策略对照如表1所示.

2)风险中性.这类供应商对于“中标概率”以及中标后获得的利益之间的偏好相当.因此，在此类投标决策支持过程中，应充分利用首价密封拍卖机制“激励相容”性质来控制供应商投标，因此该类供应商在投标时严格按照其成本函数进行投标，而无需对其投标进行调整.

3)风险偏好.这类供应商与“风险厌恶”的供应商恰好相反，他们宁愿降低自己的中标概率以提高自己在中标后的收益.与“风险厌恶”型决策支持相反，该类供应商决策支持应尽量降低投标“质量”，以增加其中标后所获得的利润.但这种策略势必会降低供应商的中标几率.

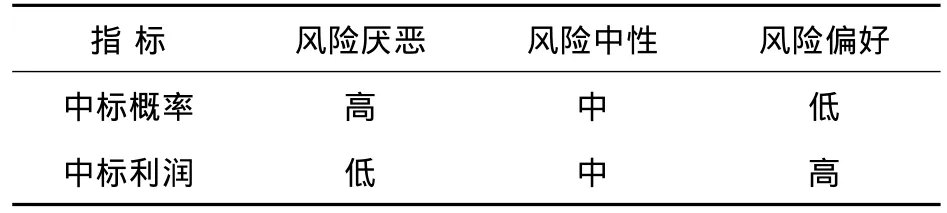
表1 供应商风险策略对照表

2 网上采购拍卖供应商投标策略分析

2.1 前提假设

由于本文所述供应商决策支持是在“分包算法”大背景下建立的，因此该决策模型应满足文献［10］所述的前提假设，此外还应满足下列假设:

假设1 先验信息可以准确反映供应商偏好信息.

假设2 采购方与供应商的效用函数均为线性的，且各属性之间均是独立可加的.

假设3 假设供应商都是逐利的，因此在供应商决策支持时应充分考虑供应商 Sj对包Bundlek的估价函数vjk及投标成本函数bvjk的取值，从而满足中标后获利为正，即

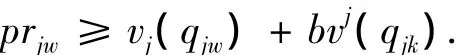
假设4 投标者的投标策略、分包的估价、成本函数及投标成本函数均为其私有信息，不受其他投标者影响.

2.2 符号说明

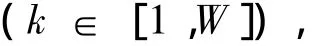
利用 Idealk表示 RFQ过程中针对分包Bundlek的最优投标，即价格属性与非价格属性均最优的投标.其 中:BBundlejk*为本文为供应商提供的决策支持解;prjw为供应商投标中的价格属性值;qjw={qjw1，qjw2，…，qjw(p－1)}为投标中的p－1个非价格属性;prjw'和qjw'分别为专家根据指标体系对投标的评价结果.

2.3 投标策略模型

2.3.1 投标分包选择决策支持模型

首先确定投标分包Bundlej.对于供应商Sj，依据分包结果Bundle对供应商偏好集Prefj进行约减得到结果约减偏好集Preftrimj.对于允许对多个商品投标的情况，分包Bundlek可确定为Prefj

trim中的所有分包，具体分包结果为

在某些情况下，出于对投标成本的考虑，供应商不会对偏好集Preftrimj中的所有分包进行投标，为此需要从分包结果以及偏好集2个方面综合考虑为供应商提供投标分包选择支持，设结果最终偏好集Prefstj.设与Prefstj对应的偏好权重记为wstj集，供应商Sj在偏好集Prefstj中对Bundlek的偏好强度记为wstjk，在供应商决策支持模型中，应该以供应商利益最大化为目标，因此计算wstjk为

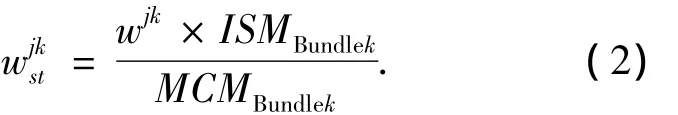
式中:MCMbundle，ISMbundle分别为分包 Bundle的“供应商竞争性度量”以及“包内商品相似性度量”，采用基于先验数据的计量经济学方法进行计算;wjk为依据偏好集Prefj计算出的Bundlek权重值，具体计算方法为:

1)计算Prefj中Bundlek的排序Seqjk值.计算方法为:

2)依据Seqk计算wjk为

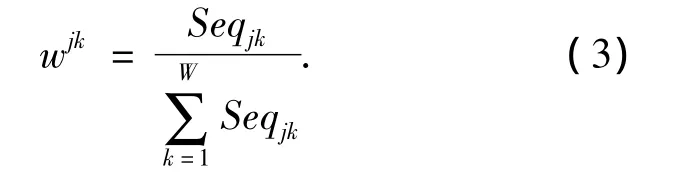
式中:wjkst越大表明供应商对其偏好程度越大，越应该对其投标.其原因在于:1)在最终分包确定过程中应该考虑供应商最初偏好情况wjk，因此应将wjk做为分子，以保证其越大越好;2)同理，如果包内商品相似性越大表明分包所带来的规模效

2.3.2 投标属性值确定决策支持模型

确定供应商Sj对于集合Bundlej中各分包Bundlek的投标属性，包括价格属性prjk和非价格属性qjk.设风险决策系数为ε(ε∈( 0，1))，其中ε为供应商风险意识的大小，ε越大表示其越偏好风险，反之则越厌恶风险.当ε=0.5时，供应商为风险中性;ε∈( 0，0.5)时，供应商为风险厌恶的;ε∈(0. 5，1.0)时，供应商为风险偏好的.

在实际应用中，供应商依据自身对“中标概率”及对“中标后所获得利益”之间的偏好强弱来确定自己的风险偏好类型以及风险决策系数ε的值，具体区分方法可以借助风险决策系数表来设定，如表2所示.益越大，供应商的供应成本会因此降低，因此在式(2)中可将ISMbundle做为分子计算，以保证其越大越好;3)在供应商投标时应尽量避免对高竞争性的分包进行投标，原因在于分包竞争性越高，竞争越激烈，供应商中标几率越低，中标后的收益越小.因此在式(2)中将MCMbundle做为分母，以保证供应商竞争性越小越好.

式(3)可以满足供应商在投标过程中收益最大.特别地，对于只允许供应商对唯一商品投标且不计投标成本的情况，在决策支持过程中为供应商提供的分包建议分包结果为议解为BBundlejk*=BBundlejk;若供应商Sj的投标BBundlejk与Idealk的欧氏距离不为 0，则应依据lenjk的大小以及风险偏好强度设置降价幅度，具体规则为:BBundlejk与Idealk的欧氏距离lenjk越大，降价幅度越大，反之则越小;供应商越偏好风险则降价幅度越大，反之则越小.因此，建议解BBundlejk*的价格属性pr*jk(1)为

表2 风险决策系数表

1)“风险厌恶”型供应商解策略支持模型θ(1).由于风险厌恶型供应商愿意牺牲中标后的利益以换取更大的中标可能性，因此在决策支持时，首先应该依据其投标结果BBundlejk(prjk，qjk)与RFQ过程中最优投标Idealk为供应商提供决策支持.

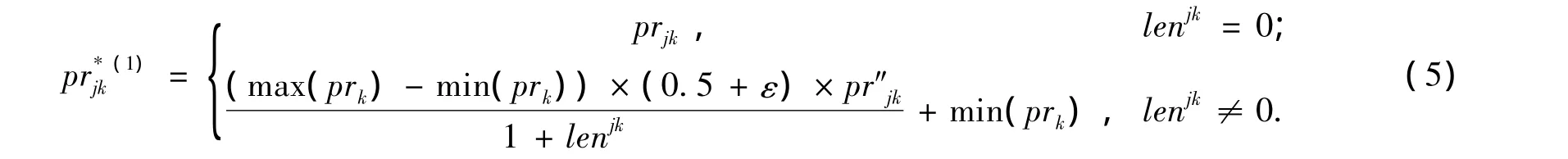
若供应商Sj的投标BBundlejk与Idealk的欧氏距离为 0，则表明BBundlejk是最优投标，此时建式中:pr*k为Idealk中对Bundlek投标的最优价格属性;max函数，min函数分别为求最大和最小实数的函数;prk为对Bundlek投标中的所有价格属性的集合.由于ε ∈( 0，0.5)且 lenjk∈［ 0，1］，可满足投标价格建议解pr*jk(1)小于供应商投标价格pr'jk，因此该投标决策支持是有效的.具体推导过程为

由于供应商在投标过程中必须保证中标后收益为正，因此在计算最优投标价格时应考虑投标价格与成本之间的关系，因此需对prjk*进行调整为

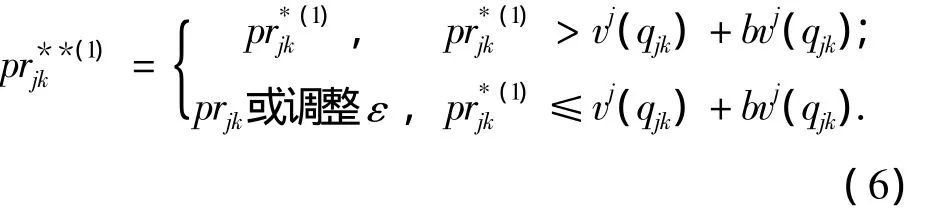
因此，最终建议解为 BBundlejk*=(prjk＊＊(1)，qjk).在此仅考虑对价格属性进行支持，而非价格属性则保持不变.其原因在于:①非价格属性qjk情况比较复杂(即包含数值数型又包含非数值属性)，对其进行决策支持存在一定困难;②此外，供应商的风险偏好关注的是“中标可能性”与“中标后的利益”之间的关系，如果保持qjk不变而降低投标价格prjk可以满足“风险厌恶”供应商增加“中标可能性”降低“中标后利益”的要求;③在实际应用中待采购商品的非价格属性通常相对固定.因此，这种建议解是合理的.

2)“风险中性”型供应商解支持θ(2).由于“风险中性”型供应商对于“中标概率”以及“中标后利益”偏好相同，因此其投标决策支持相对简单，即与原投标保持一致，投标决策值为(prjk*(2)，qjk).其投标价格为

3)“风险偏好”型供应商策略支持模型θ(3).对于该类供应商来说，相比中标概率而言其更看重中标后的利益.因此，对该类供应商的决策支持与“风险厌恶”供应商恰好相反，应增加其中标后收益，即提高其投标价格prjk.若当前供应商所投标为最优，即BBundlejk与Idealk的欧氏距离为 0，此时中标可能性很大，因此降低采购成本;若BBundlejk非最优投标，此时供应商投标不变.计算结果为

由于该类决策支持过程中满足prjk≤pr*jk并且在分包确定阶段已经满足供应商收益为正，因此无需对pr*(3)jk进行调整.投标决策值为(pr*(3)jk，qjk).

3 投标决策支持实例演算

3.1 算例数据描述

假设某生产企业要从3位供应商那里采购5 种商品(ai，i∈［ 1，5］).其中:S1为风险厌恶的供应商;S2为风险中性的供应商;S3为风险偏好的供应商.供应商投标数据以及分包数据按照文献［10］中的拆分包算法规则随机生成.其对应初始偏好集分别为Pref1、Pref2以及Pref3，约减偏好集分别为Pref1trim、Pref2trim以及Pref3trim，最终偏好集分别为Pref1st、Pref2st以及Pref3st.

3.2 分包确定决策支持

以供应商Sj为例进行算法演示.步骤为:

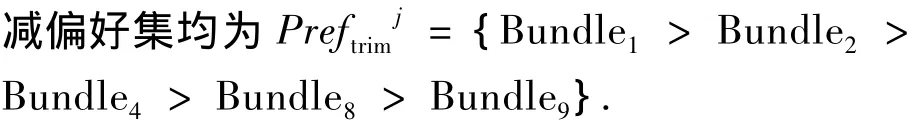
2)计算Prefstj.利用文献［10］所述拆分包算法计算得到的Prefjtrim中各分包所对应的ISMbundle以及MCMbundle值. 如文献［10］所述，ISMbundle以及MCMbundle之间无相关性，因此表3中的数据依据一定规则随机生成;wjk值则由算法1计算获得.接着，根据式(2)计算得到wstjk值，此时偏好集合Prefst

j={Bundle4＞Bundle2＞Bundle1＞Bundle8＞Bundle9}，相应计算结果如表4所示.

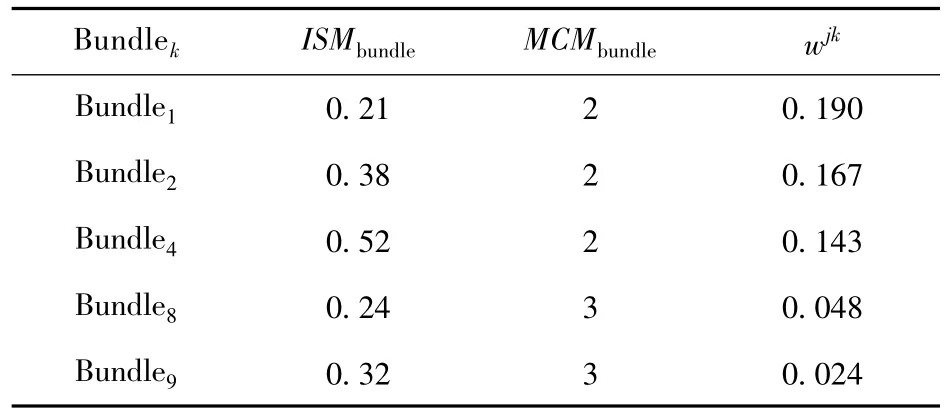
表3 各分包对应ISMbundle及MCMbundle对照表

表4 各分包对应权重wjkst

在不计投标成本bvj的情况下，假设最终采购拍卖机制允许多个投标，供应商可以对5个分包都进行投标;当采购拍卖机制只允许投1个分包的情况下，依据式(4)则系统建议投标分包为Bundle4.

3.3 投标属性确定决策支持

在确定好供应商投标分包以后，不同风险偏好的供应商的投标策略不同.利用3类算例分别对3类风险偏好的供应商的投标决策支持进行如下描述:

1)风险厌恶型供应商决策支持算例.设“风险厌恶型”供应商S1的风险偏好是先考虑获胜概率，而不是获胜后利益，且保证赢得本次拍卖的意愿介于较强和一般之间，本文在区间［0. 250，0.375］(参照表2)之间随机生成风险系数ε1为0.3.下面对供应商决策支持模型θ(1)对S1进行决策支持.由于本投标属性决策支持模型是对于确定投标分包的价格属性进行决策支持，因此所述算例仅以1个分包为例进行算法描述.

为了叙述简便，本节沿用分包Bundle.设各供应商针对于分包Bundle3( 3，4)的投标结果如表5所示.其中，非价格属性qjk为最终非价格属性打分之和，价格属性 prjk为各供应商对分包Bundle3的出价，在此假设价格打分prjk'与prjk相等.在采购方看来，待采购商品价格越低越好，非价格属性越高越好，因此Ideal3={ 0，1}.

表5 各供应商对分包Bundle3投标情况

具体计算步骤为:

①计算供应商S1的投标与Ideal3之间的欧氏距离len13为

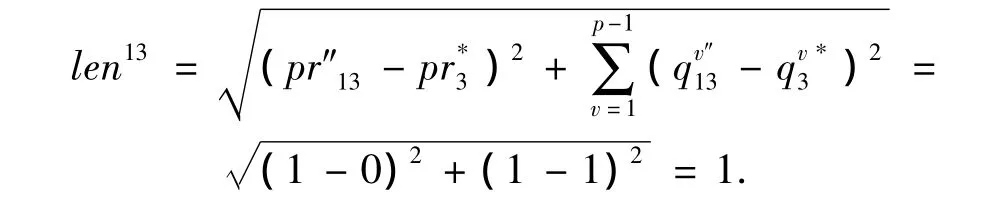
② 由于len13不为 0，依据式(5)计算建议投标价格prjk*(1)，计算结果为

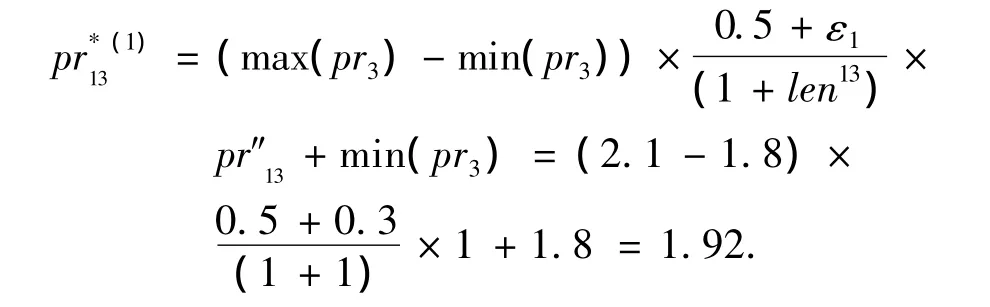
③由于供应商投标价格属性建议解pr*(1)jk相比原投标价格属性prjk有所降低，因此应依据式(5)所示计算建议解pr1*3(1)与供应商成本之间的关系，以保证供应商投标盈利.若不满足可以重新设置偏好值重新计算pr*jk(1)，或者选择保持原价格属性投标值prjk不变.

2)风险中性型供应商决策支持算例.设“风险中性型”供应商S2的风险系数ε2为0.5(如表2所示).供应商S2的投标情况如表4所示.依据“风险中性”供应商决策策略θ(2)中的式(6)可得:

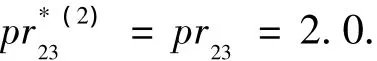
3)风险偏好型供应商决策支持算例.设“风险偏好型”供应商S3的风险偏好是先考虑获胜后利益，而不是获胜概率，且保证获胜后利益最大化的意愿较强，参照表2可得风险系数ε3为0.75.依据风险偏好型供应商决策支持策略θ(3)计算过程为:

①计算供应商S3的投标与Ideal3之间的欧氏距离len33，计算为

②由于len33不为零，因此供应商投标价格与原投标价格保持一致，即

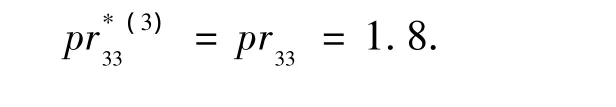
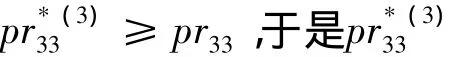
4 结论

1)依据风险策略及偏好对当前参与采购拍卖供应商投标策略进行分类，为供应商投标策略模型的建立提供依据.

2)在科学计量学分包算法以及首价密封拍卖机制基础上，利用投标行为分类及偏好集理论算法设计供应商投标分包选择以及投标属性值确定决策支持模型.

3)算例演示结果表明:该方法可以有效地提高供应商的收益、降低拍卖过程中信息不对称所带来的负面影响.

［1］ GWEBU K.Decision support in multi－attribute reverse auction［J］.Journal of Electronic Commerce Research， 2009，10(4):252－264.

［2］CHEN Peiyou，ZHAO Wenmei.The design of interactive multi－attribute reverse auction system［C］//CCDC＇09 Proceedings of the 21st Annual International Conference on Chinese Control and Decision Conference.Washington，DC:IEEE，2009:4036－4040.

［3］JAP S，HARUVY E.Interorganizational relationships and bidding behavior in industrial online reverse auctions［J］.Journal of Marketing Research， 2008，45(5):550 －561.

［4］JAP S.The impact of online reverse auction design on buyer－supplier relationships［J］.Journal of Marketing， 2007，71(1):146－159.

［5］ABRACHE J，CRAINIC T G，GENDREAU M，et al.Combinatorial auctions［J］.Annals of Operations Research， 2007，153(1):131－164.

［6］GAREY M R，JOHNSON D S.Computers and Intractability:A Guide to the Theory of NP－completeness［M］.San Francisco:Freeman，1979.

［7］Rothkopf M H，PEKEC A，HARSTAD R M.Computationally manageable combinational auctions［J］.Management Science， 1998，44(8):1131－1147.

［8］黄河，徐鸿雁，陈剑.多因素采购组合拍卖获胜者确定问题研究［J］.系统工程理论与实践， 2008，28(7):27－33.

［9］陈剑，黄河.基于树型结构的在线逆向组合拍卖模型［J］.系统工程理论方法应用， 2004，13(4):310－315.

［10］HU Dayong，FENG Yuqiang.Research on post－bidding bundle strategy for reverse auction［C］//17th Annual Conference Proceedings of 2010 International Conference on Management Science ＆ Engineering.Washington，DC:IEEE，2010(1):51－57.

［11］呼大永，冯玉强.两阶段反向组合多属性拍卖分包算法［J］.哈尔滨工程大学学报(自然科学版)， 2010，31(12):1649－1654.

［12］傅丽芳.网上组合拍卖机制设计与投标模型研究［D］.哈尔滨:哈尔滨工业大学，2008.

［13］BERTSIMAS D，HAWKINS J，PERAKIS G.Optimal bidding in online auctions［J］.Journal of Revenue ＆Pricing Management， 2009，8(1):21 －41.

［14］陈剑，陈熙龙，宋西平.拍卖理论与网上拍卖［M］.北京:清华大学出版社，2005.

Suppliers’bidding decision support model for online reverse auction

HU Da－yong1，FENG Yu－qiang1，FU Ming1，QU Yun－bo2

(1.School of Magagement，Harbin Institute of Technology，150001 Harbin，China，superhudayong@163.com;2.Harbin Industry and Art Design School，150059 Harbin，China)

To solve the suppliers’support problem of online reverse combinatorial multi－attribute auction based on bundling，a bundling confirmation model and suppliers’bidding strategy are proposed based on the scientometrics bundling algorithm and the analysis of suppliers’bidding behavior in order to maximize the revenue of the suppliers.After that，an illustration for this model is presented，and the result shows that this model can significantly improve the suppliers’revenue and reduce the negative effect from the asymmetric information during the auction.

reverse auction;combinatorial multi－attribute auction;decision support;bidding strategy model

F253.2;F724.59

A

0367－6234(2011)09－0095－06

2011－02－01.

国家自然科学基金资助项目(70572023);黑龙江自然科学基金重点资助项目(zd200803－01).

呼大永(1983—)，男，博士研究生;

冯玉强(1961—)，女，教授，博士生导师.

(编辑 张 红)