厦门翔安海底隧道风化槽衬砌结构可靠度分析
郭小红
(中交第二公路勘察设计研究院有限公司,武汉 430056)
0 引言
结构可靠度的研究始于20世纪初,随着科学研究的不断深入和计算机技术的不断发展,在地面工程结构设计中采用可靠度设计方法已取得了实质性的进展并达到了实用阶段。作为以复杂的岩土体为对象的地下工程,由于其力学性质具有很大的不确定性(随机性和模糊性),特别是对地下结构施工中的变异性缺乏统计资料,其结构的可靠性评定比地面结构更为复杂。近十几年来,国内外同行专家、学者在这方面作了一定的研究[1-5]。
1956年,A Casagrande提出了土工和基础工程中的计算风险问题。国际岩石力学学会实验室和现场测试标准化委员会(ISRM)提出了“岩石力学试验建议方法”,作为试验规程的重要蓝本。A Longinow等人在研究人防工程结构可靠性时,就动载作用下防护结构可靠性的设计理论作了大量的工作,并提出了RDBF可靠性设计方法。我国铁路部门也于20世纪70年代对隧道及地下工程的可靠度进行研究,一些大专院校的专家和学者从现有的工程收集了大量的数据,从荷载的分布、弹性抗力系数、明洞荷载等方面进行了统计分析,提出了相应的统计计算公式[6]。20世纪80年代至今,我国有关部门已对地下结构按可靠度设计进行了大量探索,但要在设计中广泛应用,尚需进一步完善[7-8];特别是在公路隧道的设计中,还基本未涉及到可靠度理论。
厦门海底隧道是迄今采用钻爆法施工的最大断面海底隧道,全长6.05 km,最大水深35 m。在海域地段,隧道共穿越了4条累计长达300 m的风化深槽。该地段围岩软弱、破碎,给衬砌结构的设计方面带来一系列问题。结合厦门海底隧道设计中的技术特点,研究风化槽围岩段隧道衬砌结构的稳定性和可靠性具有重大的理论意义和工程应用价值。
影响海底隧道衬砌可靠度的因素有3个:1)环境因素。即地质条件,如岩石的基本性质、岩体的结构状态、海水状态及海水对结构物的侵蚀、初始应力状态等为地质状态的影响因素。2)结构材料。即混凝土、钢筋等。3)施工工艺。即人为因素,如施工方法、支护措施、隧道形状及尺寸等。由于勘察的困难、荷载的变化复杂性、海水腐蚀作用、岩体力学参数的不确定性等,使得人们更加难以采用传统的定值分析方法研究跨海隧洞衬砌稳定性问题。因此,开展海底隧道各种不确定因素及其对隧道稳定性影响的可靠度研究具有十分重要的意义,不仅对将来海底隧道的设计和施工具有直接的指导作用,还能对山岭隧道、水底隧道的设计和施工起到十分重要的借鉴作用。
1 海底隧道基本随机变量统计特征
影响衬砌结构可靠度的基本随机变量主要有竖向荷载、侧压力系数、水压力、围岩弹性抗力系数、衬砌混凝土的容重、混凝土的抗压极限强度、混凝土的抗拉极限强度、混凝土的弹性模量、衬砌厚度以及计算模式不定性等。由于缺乏现场足够的试验样本,本次可靠性计算参考《公路工程结构可靠度设计统一标准》《公路隧道设计规范》《公路隧道设计细则》以及铁路隧道可靠性研究资料中的相关参数的统计特征。对隧道竖向松弛荷载、侧压力系数、衬砌水压力、弹性抗力系数k、喷射混凝土物理力学指标、二次衬砌混凝土物理力学指标统计特征如表1—6所示。
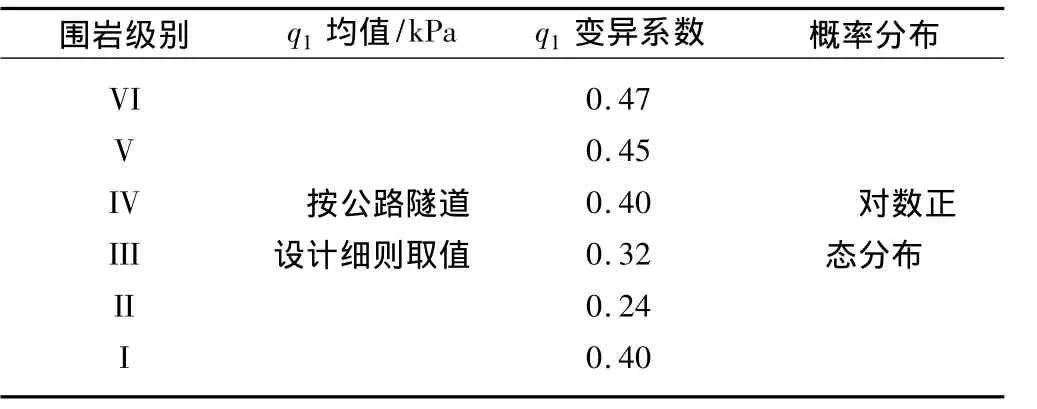
表1 隧道竖向松弛荷载统计特征Table 1 Characteristics of vertical relaxation load of tunnel
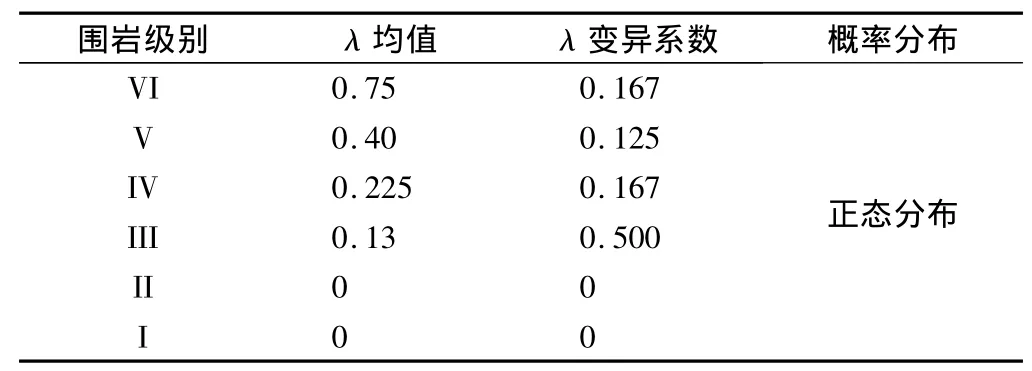
表2 隧道侧压力系数统计特征Table 2 Characteristics of lateral pressure coefficient of tunnel
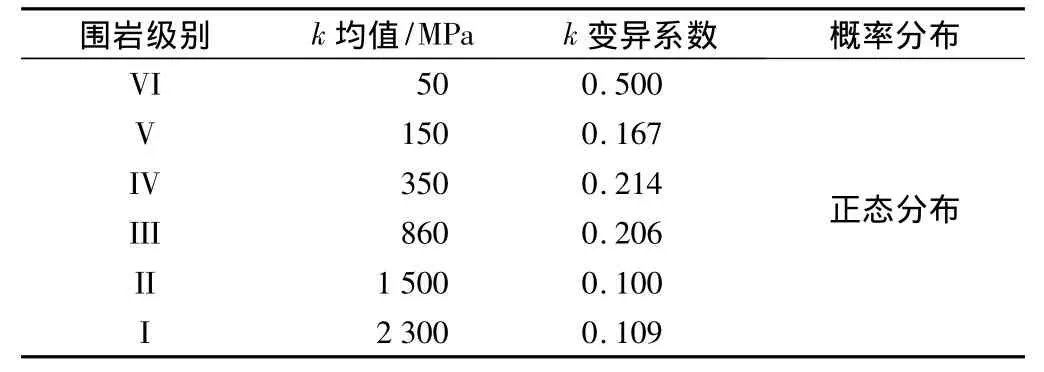
表3 弹性抗力系数统计特征Table 3 Characteristics of elastic resistance coefficient
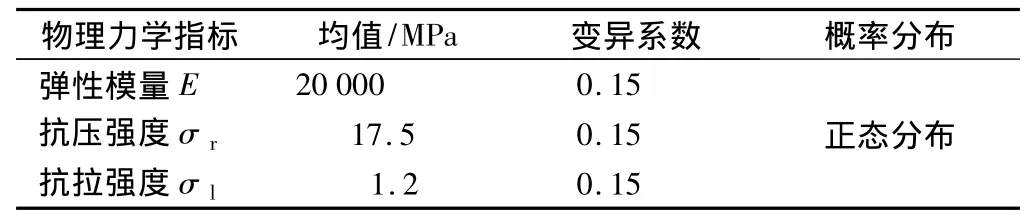
表4 喷层材料物理力学指标统计特征Table 4 Physical and mechanical characteristics of shotcreting shell
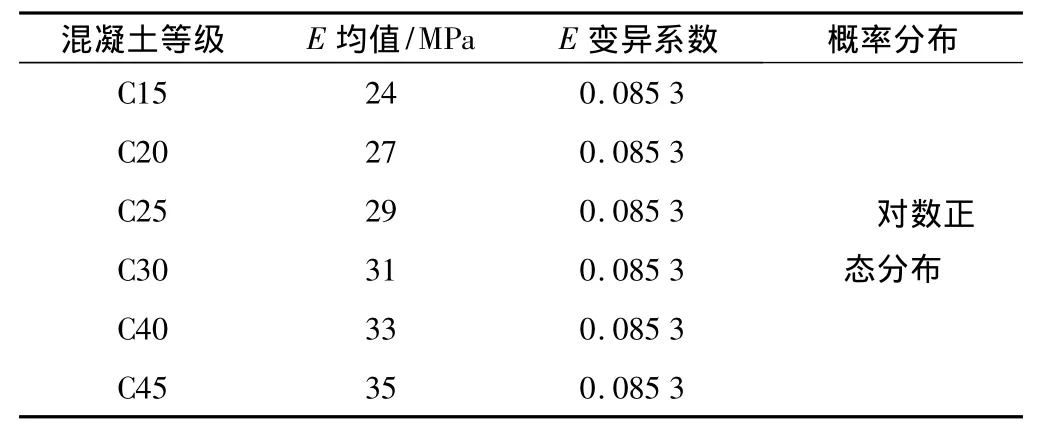
表5 衬砌混凝土弹性模量统计特征Table 5 Characteristics of elastic modulus of lining concrete
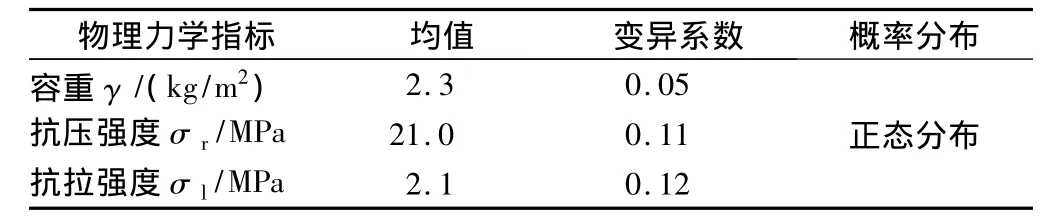
表6 衬砌混凝土物理力学指标统计特征Table 6 Physical and mechanical characteristics of lining concrete
对于风化槽海底隧道,采用全封堵防水衬砌方案,衬砌水压力
q2=全水头×α。
式中α为水压折减系数。其统计特征假设为:均值μα=1.0,变异系数δα=0.2,概率分布为正态分布。
2 结构内力敏感度分析
取厦门海底隧道最深风化槽截面作为分析对象,建立平面计算模型。根据施工设计图,二次衬砌厚度拱顶处为0.7 m,仰拱处为1.1 m,边墙处为0.7~1.1 m(均匀变化),将结构划分为164个梁单元(见图1)。
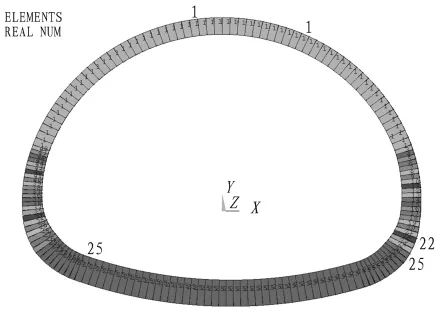
图1 荷载结构法二次衬砌模型图Fig.1 Model of secondary lining simulated by load-structure method
应用拉丁超立方抽样法(LHS)随机抽样得到的一组随机数代入有限元方程求解,得到一组响应变量的解,最后将这组解进行统计分析,从而得到该响应变量的分布特征。
通过计算可得到不同荷载组合情况下的二次衬砌结构的轴力和弯矩(见图2和图3)。
根据随机有限元法得到关键界面的轴力、弯矩和偏心距作为荷载结构法结构可靠性计算的响应量。隧道衬砌关键点的轴力、弯矩和偏心距的统计规律如表所示。
计算结果表明:单元85处截面的偏心距值最大,单元112处截面的负弯矩最大,单元138处截面的正弯矩和轴力值均为最大。分别取这5个截面处的轴力、弯矩和偏心距作为可靠性分析的响应量,分别对轴力、弯矩和偏心距对随机变量的灵敏性开展分析,将以最大轴力、最大弯矩和最大偏心距的位置作为结构可靠性分析的重点。
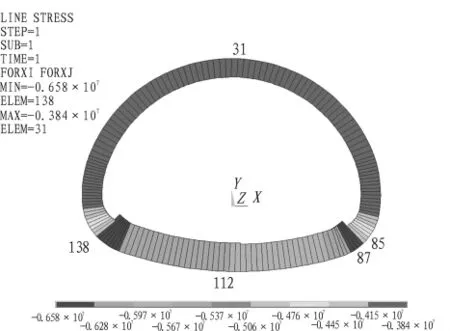
图2 二次衬砌轴力分布(单位:N)Fig.2 Distribution of axial force of secondary lining(N)
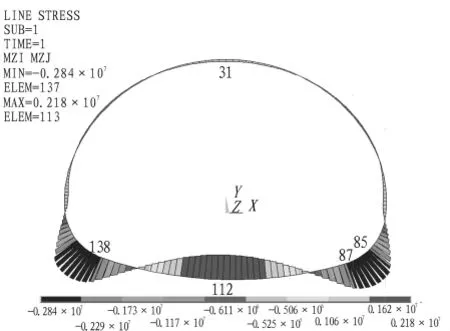
图3 二次衬砌弯矩分布(单位:N·m)Fig.3 Distribution of bending moment of secondary lining(N·m)
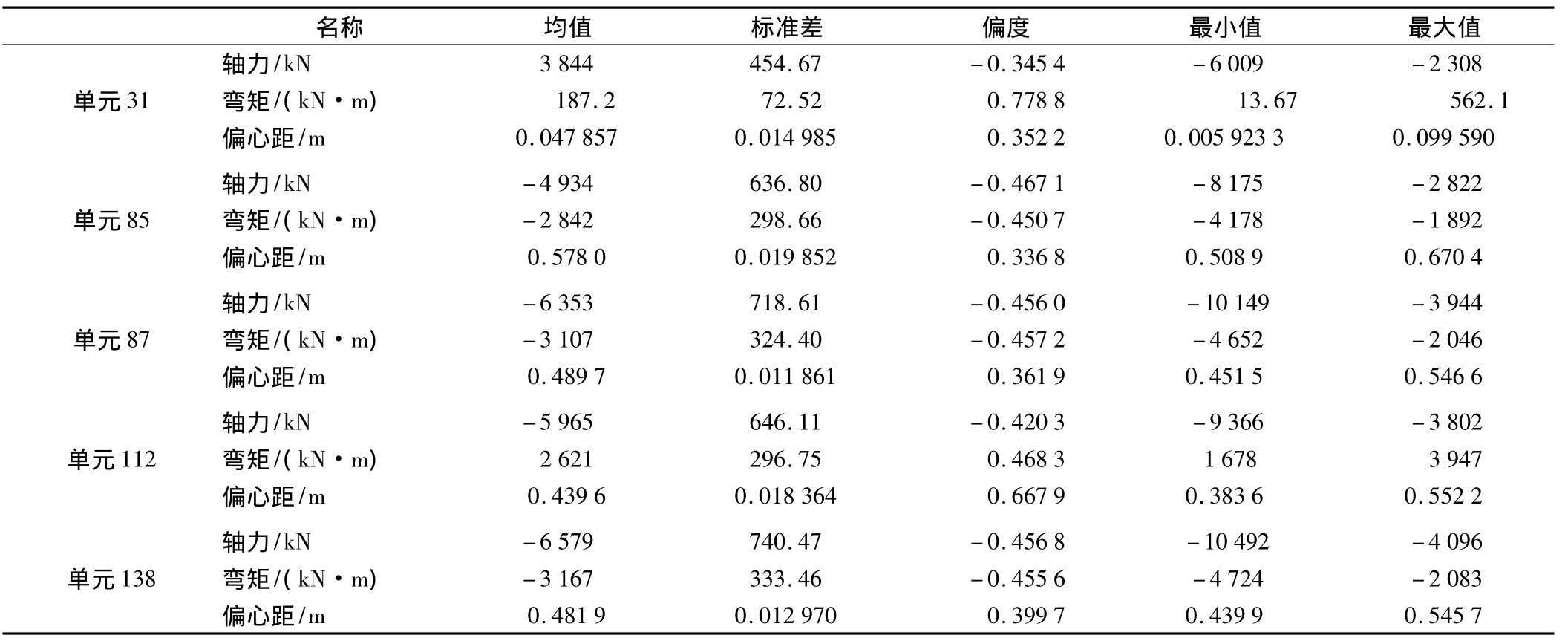
表7 衬砌结构可靠性计算响应量统计特征Table 8 Statistics of responses in reliability calculation of lining structure
单元138最大轴力关于随机变量的功能函数表示为Fmax=-6 582 543+26 902.64×E_scaled-52 783.63×k_scaled-441 352.3×Hw_scaled+2 072.244×λ-
603 862.9×Hs_scaled-932.593 2×E_scaled2+
5 128.851×k_scaled2-340.741 4×Hs_scaled2。
式中:E_scaled=3.334 574×10-10×E-11.671 03,
k_scaled=1.923 382×10-8×k-6.097 04,
Hw_scaled=0.237 708 7×Hw-8.319 638,
λ_scaled=19.994 23×λ-7.997 607,
Hs_scaled=0.333 270 4×Hs-3.665 974。
单元138的轴力统计分布见图4。
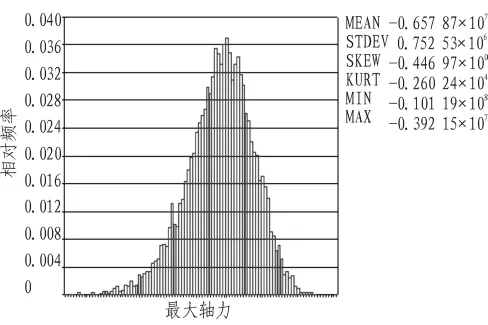
图4 单元138轴力统计分布图Fig.4 Distribution of axial force of element 138
单元138最大弯矩关于随机变量的功能函数表示为
Mmax=-3 165 053-23 166.47×E_scaled+44 940.49×
k_scaled-194 078.3×Hw_scaled+8 380.934×λ-274 237.8×Hs_scaled+1 120.621×E_scaled2-3 104.173×k_scaled2+346.582 2×Hs_scaled2。
式中:E_scaled,k_scaled,Hw_scaled,λ_scaled,Hs_scaled各参数同Fmax功能函数参数取值。单元138的弯矩统计分布见图5。
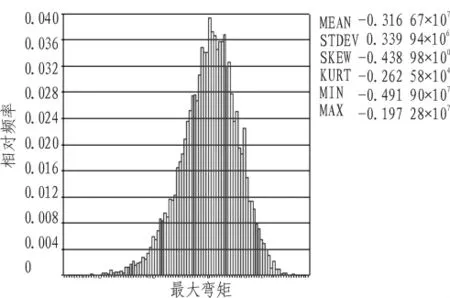
图5 单元138弯矩统计分布图Fig.5 Distribution of bending moment of element 138
通过对各随机变量的灵敏度分析,结果发现:1)衬砌结构各节点最大轴力、最大弯矩及最大偏心距受结构的覆土厚度、围岩的弹性抗力系数、外水头高度以及衬砌混凝土的弹性模量等共同的参数制约,且均对结构的覆土厚度最为敏感;2)最大弯矩比最大轴力和最大偏心距多一个影响因素,即围岩的侧向压力系数。由此可以得出:1)最大轴力和最大偏心距几乎不受围岩的侧向压力系数变化的影响;2)最大轴力和最大弯矩主要受到结构的覆土厚度和外水头高度影响,其他几个参数的影响相对较小;3)4个参数对最大偏心距的影响比较平均,相差较少。
3 结构可靠度分析
根据对各响应量的统计分析,采用蒙特卡洛方法对翔安隧道衬砌结构取单元85,87,112,138处的截面进行可靠度分析,分析时取抽样次数为2 000次。这些截面均为大偏心受压,按照大偏心受压构件的承载力复合公式,根据设计配筋量计算截面的轴力和弯矩,作为极限承载力,将其与荷载结构法计算出的单元轴力、弯矩比较,计算结构的可靠性。
当结构为大偏心时,其轴力和弯矩的设计值计算如下:
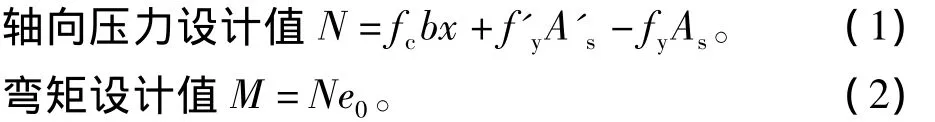
式中:fc为混凝土受压强度设计值;fy,f'y为钢筋受拉及受压强度设计值;As,A's为受拉及受压钢筋面积;e0为初始偏心距;b为截面宽度;x为受压区高度。
根据偏心受压构件的正截面强度校核方法,对中和轴的力矩平衡可知

式中:η为偏心距增大系数,当l0/h≤8,η=1,否则按式(4)—(6)求 ξ1,ξ2及 η:
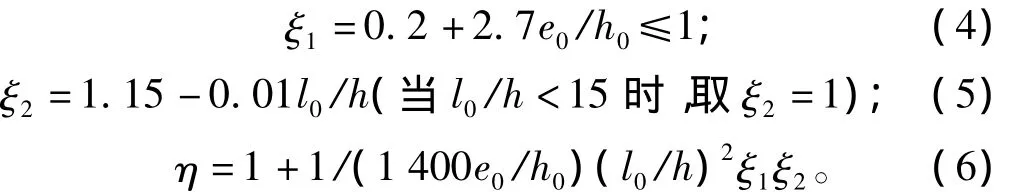
式中:l0为受压构件的计算长度,按无铰拱计算,l0=0.36S(S为拱轴线长度);h为截面高度;α,α'为截面受拉及受压区保护层厚度。
截面采用对称配筋,As=A's=4 910 mm2,钢筋强度设计值fy=f'y=310MPa,混凝土强度等级为C45,抗压强度设计值fc=21.5 MPa,混凝土保护层厚度衬砌内侧为65 mm,衬砌外侧为55 mm。
将计算所得的初始偏心距e0代入式(3)求得受压区高度x,再将x代入式(1)和式(2)得到轴力设计值N和弯矩设计值M。将求得的轴力设计值N和弯矩设计值M作为标准值,得到结构关键截面处的可靠性。根据响应面法得到的不同衬砌厚度时,隧道关键点结构可靠性计算结果见表8和表9。
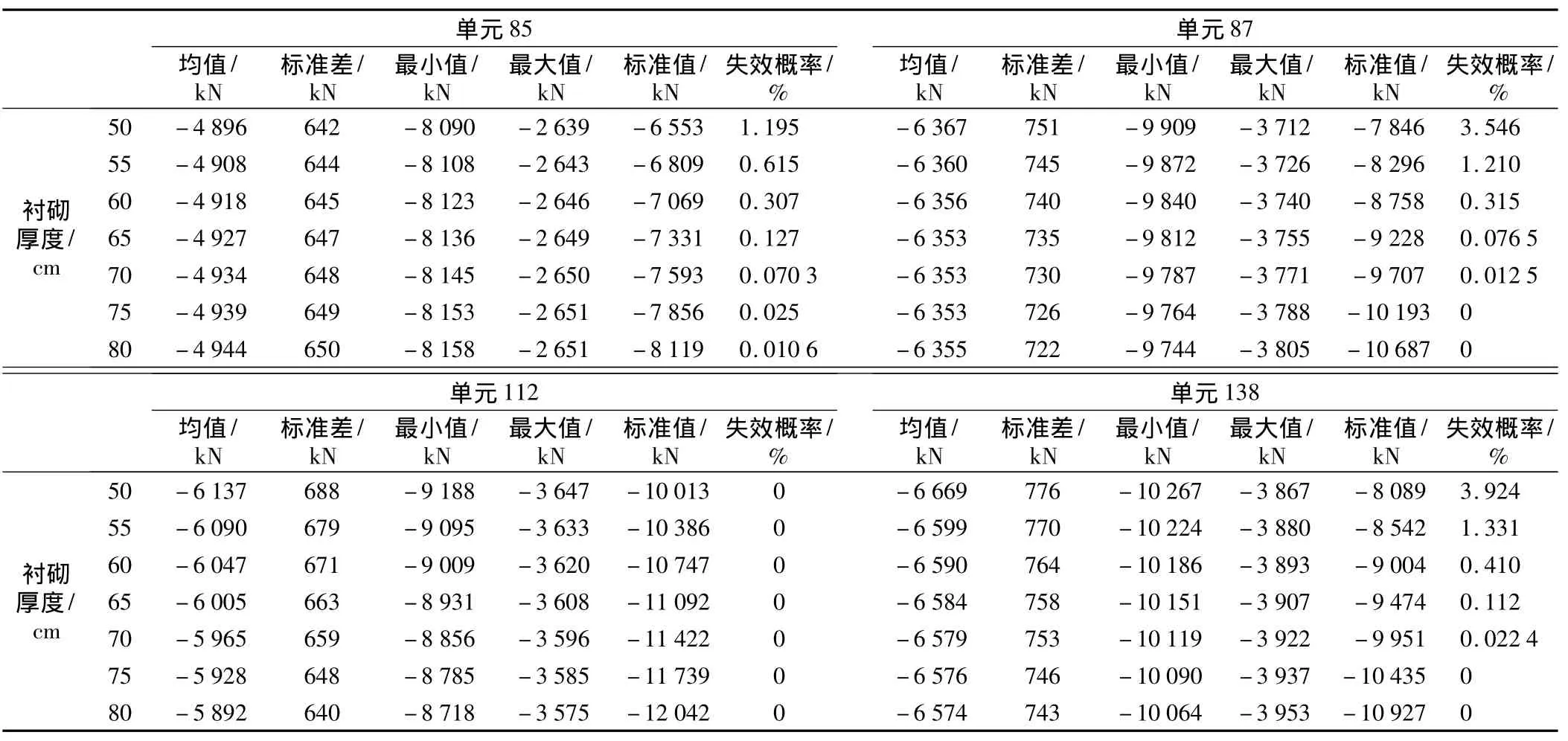
表8 不同厚度衬砌的结构可靠性轴力计算结果Table 8 Calculation results of axial force of lining structure with different thicknesses
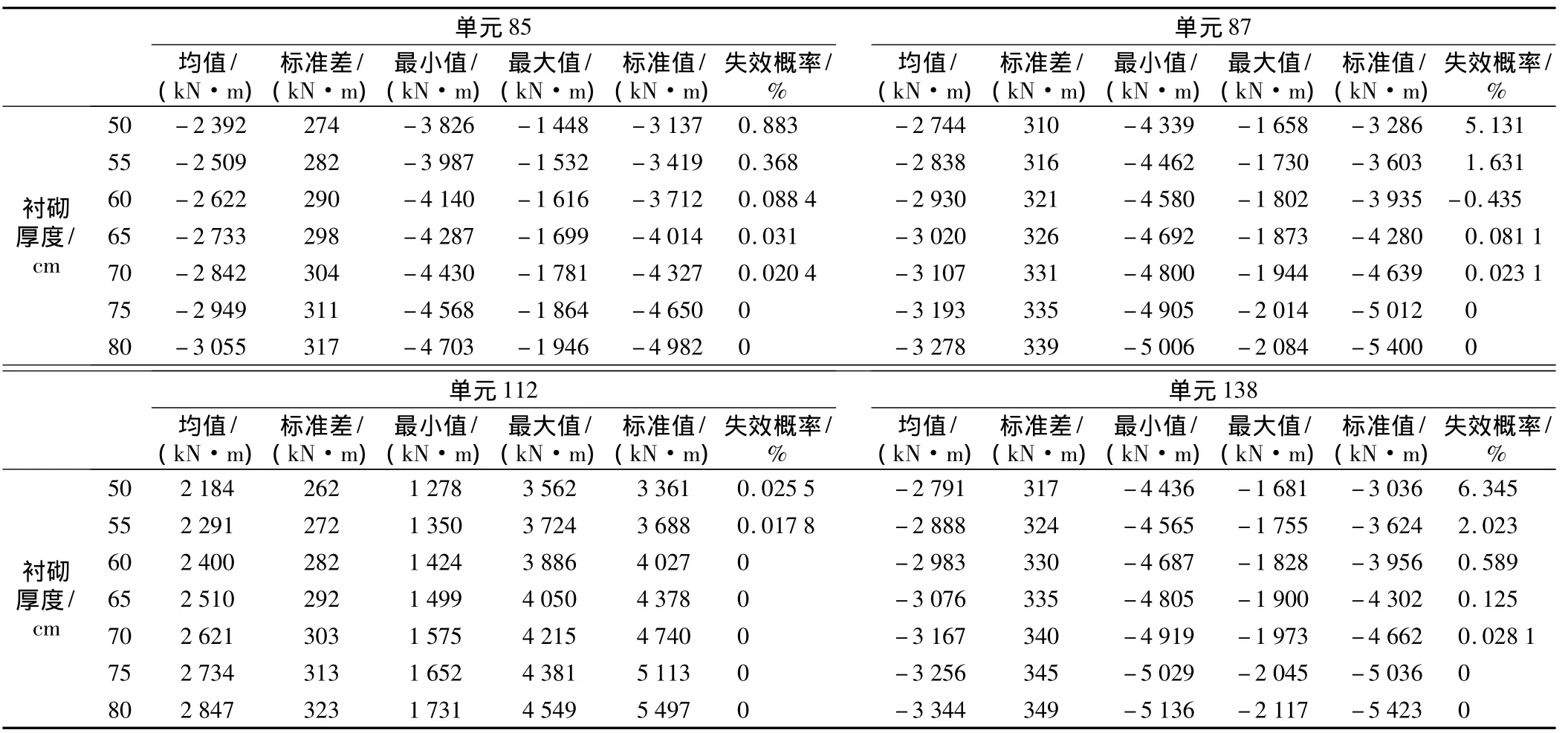
表9 不同厚度衬砌的结构可靠性弯矩计算结果Table 9 Calculation results of bending moment of lining structure with different thicknesses
表8和表9计算结果可显示:按照目前的隧道主洞70 cm的设计方案,衬砌结构关键截面的轴力和弯矩在轴力和弯矩的界限值为设计值,其可靠度指标为.20,表明风化槽隧道在目前的支护设计参数条件下,结构安全可靠。不同衬砌厚度时隧道结构的可靠度指标β如表8和表9所示。按照《公路隧道设计细则》,公路隧道结构安全等级为一级时,其目标可靠度指标为4.70,表明目前的支护结构是安全的。
4 结论
根据与隧道衬砌结构相关的参数随机统计的规律,应用拉丁超立方抽样法(LHS)随机抽样得到一组随机数,然后代入有限元方程求解,得到一组响应变量的解,最后将这组解进行统计分析,从而得到该响应变量的分布特征或直接计算结构的失效概率。通过对各随机变量的灵敏度分析,结构的覆土厚度、外水头高度、围岩的弹性抗力系数、衬砌混凝土的弹性模量以及围岩的侧向压力系数的变化对最大弯矩影响明显。其中,最大弯矩受结构的覆土厚度影响最大,其次是外水头高度。采用蒙特卡洛方法对可靠度进行求解,取抽样次数为2 000次。计算表明,在考虑潮汐荷载作用下,海底隧道二次衬砌各点并无失效,衬砌轴向应力均未超过抗拉强度和抗压强度,可靠度接近100%。
[1] 谢锦昌.铁路隧道衬砌结构可靠性分析初探[J].铁道学报,1992(1):65-70.(XIE Jinchang.A preliminary study on the reliability analysis of railway tunnel lining[J].Journal of the China Railway Society,1992(1):65-70.(in Chinese))
[2] 张弥,沈永清.用响应面方法分析铁路明洞结构荷载效应[J].土木工程学报,1993,26(2):60-68.(ZHANG Mi,SHEN Yongqing.Analysis of loading effect on railway cutand cover tunnel structure by numerical response surface method[J].China Civil Engineering Journal,1993,26(2):60-68.(in Chinese))
[3] 景诗庭.地下结构可靠度分析研究之进展[J].石家庄铁道学院学报,1995(2):13-19.
[4] 景诗庭,朱永全,宋玉香.隧道结构可靠度[M].北京:中国铁道出版社,2002.
[5] 朱永全.洞室稳定可靠性研究[D].北京:北方交通大学桥梁与隧道工程专业,1995.
[6] 张清,王东元,李建军.铁路隧道衬砌结构可靠度分析[J].岩石力学与工程学报,1994(3):209-218.(ZHANG Qing,WANG Dongyuan,LI Jianjun.Reliability analysis of liningstructures in Chinese railroad tunnels[J].Chinese Journal of Rock Mechanics and Engineering,1994(3):209-218.(in Chinese))
[7] 左勇志,刘西拉.结构动态可靠性的全随机过程模型[J].清华大学学报:自然科学版,2004,44(3):109-111,119.(ZUO Yongzhi,LIU Xila.Fully stochastic analysis method for structural dynamic reliability[J].Journal of Tsinghua University:Science and Technology,109-111,119.(in Chinese))
[8] 伍国军.公路隧道衬砌结构可靠性研究[D].北京:中国科学院研究生院,2006.

