单向不规则波群的实验室模拟和分析

刘 思，柳淑学，李金宣，俞聿修

（大连理工大学海岸和近海工程国家重点实验室，大连116024）

波群现象对于海洋工程和海岸工程具有重要意义。波群模拟的研究是与波群有关的物理和数值模型实验的前提。目前，关于随机波群的模拟研究还不成熟。Funke和Mansard［1］提出的以给定波群因子GF为波浪群性控制参数来模拟波群，但其只是就波群的高度特征而言。而事实上具有同一波群因子的波群可具有大小不同的波群长度特征。波群的高度和长度是波群特征的2个方面，这2个方面的特征都是海洋工程所关心的。Xu等［2］将波包谱的概念用于波群模拟中，建立了以给定波谱和波包谱为靶谱的波群模拟方法，认为波群特征可由波谱和波包谱两者决定，试图兼顾波群的高度和长度两方面特征来模拟，然而，其方法并未给出可供实用的波包谱，所建议的波群特征参数也不够合理，故该方法在应用上有一定的局限性，有待改进。在此基础上，俞聿修和桂满海［3］建议了合适的波群特征参数，首次提出了风浪波包谱的经验公式，在水槽中模拟出满足群高参数GFH的波群，但其依据的波包谱实测资料较少，还需进一步验证和改进。为此，作者收集了更多的实测波浪资料［4］，通过对实测波浪的群性特征参数的相关性进行分析，得到一个可反映天然海浪的波包能量分布的波包谱经验公式。

本文基于作者对海浪波包谱的研究成果［4］，同时采用群高参数GFH和群长参数GLF来表征波浪的群性，以波谱和波包谱为靶谱，建议了单向不规则波群的物理模拟方法，使模拟的波浪既满足给定的波群群性高度要求，也满足波群长度要求。

1 不规则波群的数值模拟

海浪可看作一平稳随机过程，它可由多个不同周期和不同随机初位相的余弦波叠加而成

式中：随机相位εi为［0，2π］内均匀分布的随机数［5］；ωi为各组成波的频率；各组成波振幅 ai由给定的波浪频谱确定，即

式中：s（ω）为频谱；Δωi为频率划分间隔。

对实测波浪资料进行波包谱分析［4］发现，具有不同群性的波浪其波包谱差别很大，而其频谱基本相同。这说明波群模拟只模拟波浪频谱是不够的，还需要另一个谱或参数来模拟相位谱，事实上，海浪的波包谱包含了波群的重要信息。

Funke和Mansard［1］建议用瞬时波能过程线SIWEH来模拟相位谱，但是其只采用了表征群高特征的参数GF。文中用波包来描述波群，用波包谱作为靶谱来模拟相位谱。模拟中，以合田改进的JONSWAP谱［6］作为频谱的靶谱，以作者建议的适于风浪的改进的波包谱［4］作为波包谱SA（f）的靶谱，即

式中：m0η为波谱的零阶矩；fP和fPA分别为波谱的峰频与波包谱峰频。分别为表征波浪群性高度和长度的参数，称为群高和群长参数［4］。式中σA和分别为波包线的方差和均值，可见，该公式包括群高与群长两方面的因素，模拟中可通过给定不同的波包靶谱参量GFH和GLF来控制波浪的群高和群长特征。

为了在试验水槽中产生所要求群性的波浪，首先给出采用上述波包谱数值模拟不规则波波群的方法，其基本模拟过程如下：

（1）采用JONSWAP谱和上述式（3）和式（4），计算给定波要素和群性参数下的波浪频谱Sη（f）和波包谱SA（f）；由式（1），分别以Sη（f）和SA（f）为靶谱按不规则波浪的数值模拟方法产生随机波列η′（t）和ηA（t）；

（2）计算波包线A1（t）=ηA（t）+1，其中，m0η为频谱Sη（f）的零阶矩；

（4）最后，由波包线和相位函数可构造出波列η1（t）=A1（t）cos[ φ（t]）。

可以看出，此方法的基本出发点是给定一波谱后，通过给定群高参数和群长参数，利用式（3）和式（4）就可得出一个相应的波包谱，再利用波谱和波包谱可构造出波包线和相位谱，进而就可模拟出满足给定波谱和波包谱要求，亦即满足波要素和群性要求的波列。注意到，模拟中虽不是严格地模拟不规则波列，但波浪的相位谱由波包谱控制，使得模拟的波列满足给定的群高和群长要求。此外，计算中1和φ（t）使得波列η1（t）的波能量和平均波周期与η′（t）相同，符合波浪参数的模拟要求。

为了说明上述模拟方法的有效性，作为示例，图1给出了GFH=0.7，GLF=10时模拟所得频谱、波包谱与相应目标谱的比较以及模拟的波面和相应的波包线，其中波谱为JONSWAP谱，波浪的有效波高H1/3=0.07 m，有效周期TH1/3=1.5 s，JONSWAP谱的谱峰升高因子γ=3.3，水深d=0.5 m。由图1可以看出，模拟波浪的频谱、波包谱与给定的频谱和波包谱基本一致，结果是比较理想的。大量模拟实例表明，按照上述方法，如果波要素和波群参数GFH和GLF给定，即可模拟得到同时满足给定波群群高和群长两方面要求的不规则波群。

2 不规则波群的实验室模拟

在实验室中产生不规则波波群，即模拟可以控制波浪群性的波浪，对波浪与海洋工程结构物的作用及波群特性的研究都非常重要。文中在上述数值模拟不规则波群方法的基础上，提出了可在试验水槽内指定位置产生满足群性要求不规则波波浪的方法。

2.1 实验设备和波浪条件

试验在大连理工大学海岸和近海工程国家重点实验室波浪水槽中进行。波浪水槽长50 m，宽3.0 m，深1.0 m。水槽配备有自行研制的不规则波造波系统，水槽的末端设有消能坡以吸收波浪。试验布置见图2。

模拟实验中，确定在距造波机x=24 m处产生所要求群性的波浪，为了研究波浪在水槽传播过程中波浪群性的变化特性，同时在距造波机5 m、13 m和18 m处布置浪高仪用于波浪的观测以分析波浪的传播特性。

试验水深d=0.5 m。考虑到波包谱的峰频值很小，波浪参数尤其是群性参数的统计稳定性受波浪历时长度的影响较大［7］，为了保证分析的准确性，采样长度取16 384个点，采样间隔0.02 s。为便于考察海浪波包谱与群性特征的关系，每次模拟中，给定相同的波浪要素：有效波高H1/3=0.07 m，有效周期T1/3=1.5 s。即在频谱一定的条件下，通过改变不同的群性参数GFH与GLF的大小，模拟具有相同的频谱，但群性不同的波列。需要强调的是，这里GFH与GLF的选取参考式（4）取值。

2.2 不规则波群造波板控制信号计算方法

实验室模拟波群时，不仅要求水槽指定位置处的波面具有给定的波谱特性，同时要具有给定的群性。在实验水槽指定位置处模拟不规则波群波浪的造波机控制信号可由前述数值模拟结果得到。即首先根据给定的波浪及波群参数，通过前述的数值计算方法，得到满足要求的数值波面过程，由此可按下述方法得到在指定位置产生所要求波浪的造波机控制信号。

将随机波数值模拟信号转化为造波板控制信号，是把造波板的运动和它产生的波浪看作一线性系统的输入和输出，以h（t）代表该系统的脉冲响应函数，以η（t）和ζ（t）分别代表指定位置处产生波浪的波面和造波板的位移，则有

对式（5）两侧作Fourier变换得

式中：H（f）是与h（t）的傅里叶变换，称为系统的频率响应函数，可以进一步写成

式中：x为水槽指定位置距造波板静止（中心）位置的距离。对于直立推板式造波机系统，产生波面的振幅a与造波板冲程e有如下关系［8］

式中：k为波数，它通过色散关系式

与频率f相联系。

由式（7）～（11）可计算出系统的频率响应函数，然后依式（6）由H（f）和Fη（f）计算Fζ（f），再对Fζ（f）进行Fourier逆变换即可得到造波板控制信号ζ（t）。

另外，由于造波机造波性能的误差，采用上述方法产生波浪的波浪频谱和波包谱以及群性参数GFH和GLF等与给定的目标值会有一定的误差，当此误差超出误差控制范围时，需要对给定的信号进行修正。具体修正的方法是根据水槽内实测波浪的频谱和波包谱与相应的目标谱比较，确定修正系数谱，即针对不同频率的修正系数，该系数谱与目标的频谱或波包谱相乘作为输入的谱，采用上述步骤重新计算可以得到修正的造波信号，之后采用新的造波信号重新造波，并采集数据分析。一般上述修正重复2～4次，可得到满意的波浪。

2.3 实验模拟波浪结果和分析

采用上述方法在实验水槽产生波浪，模拟不规则波波群波浪的位置为x=24 m。图3和图4分别给出GLF=15时GFH=0.5和0.9的实验模拟结果。图5给出GFH=0.9时GLF=25的模拟结果。同时，表1给出模拟波浪的统计分析结果，其中GF和［4］分别是基于波群研究的波能过程线法和连长方法定义的群性特征参数，m0η和m0A分别是模拟波浪的计算波谱和波包谱的零阶矩。

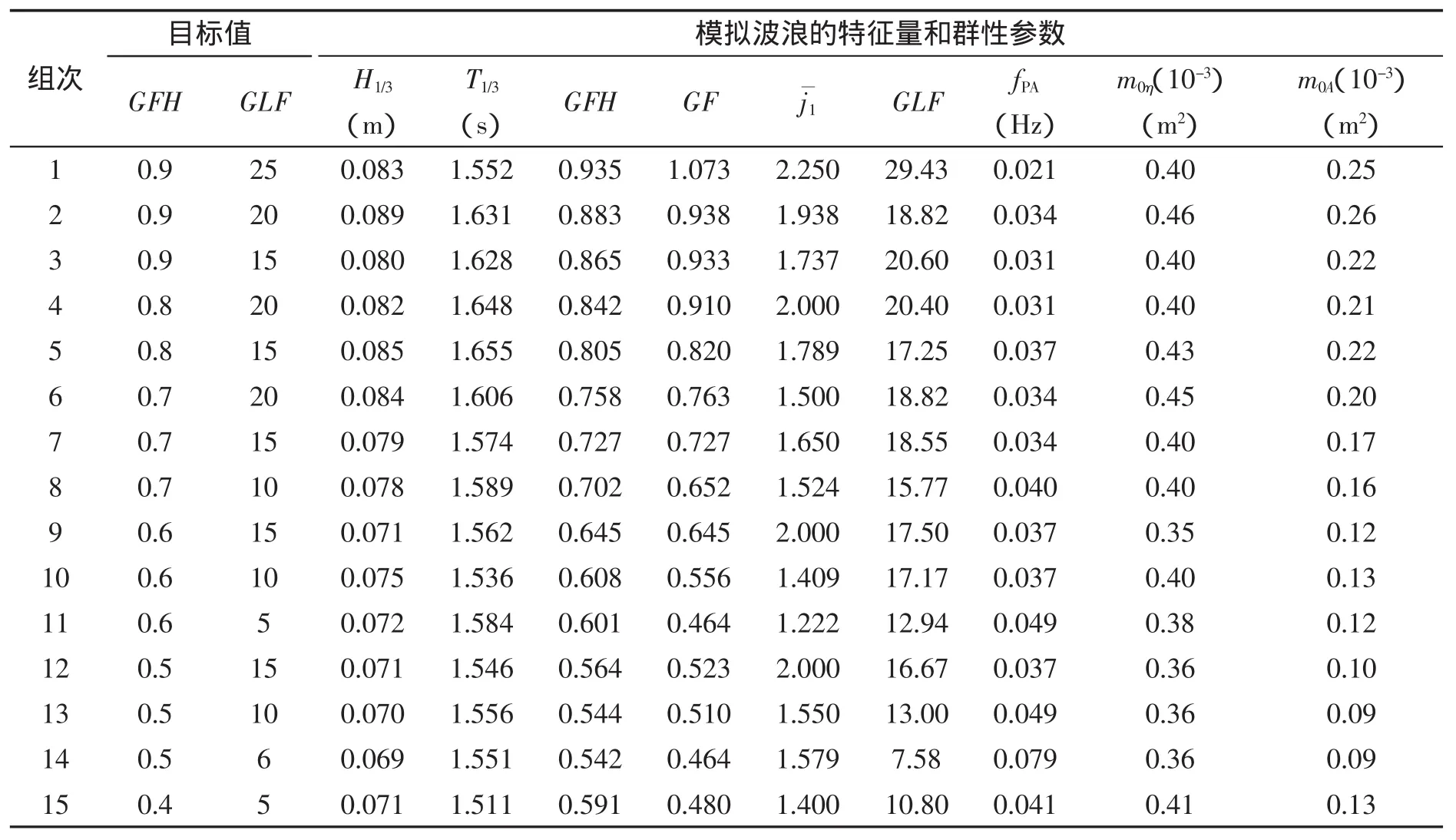
表1 x=24 m处实验模拟波浪的特征量和群性参数（H1/3=0.07 m，T1/3=1.5 s）Tab.1 Wave parameters and groupiness factors for experimentally simulated waves at x=24 m（H1/3=0.07 m，TH1/3=1.5 s）

从图3～图5和表1可以看出，模拟结果是比较理想的，即模拟实测波浪的频谱和波包谱与相应的靶谱基本一致，模拟的每组波浪满足给定波要素的同时，群高参数与群长参数的实测分析值也基本接近于目标值。按照给定的群高和群长参数，模拟得到的波面表现出相应的群性特征。因此，按照文中建议的模拟方法，可在水槽指定位置处产生同时满足给定波浪参数以及群高和群长要求的波浪。

从以上模拟实例还可以看出，参数GFH和GLF是如何由波包谱来控制不规则波群的群高和群长的。在频谱一定的条件下，一方面，给定相同GFH时，随GLF的增大，波包靶谱面积基本不变的同时峰频减小，波包变得平坦，换句话说，随GLF的增大，群长确实增大（表1）。另一方面，给定相同GLF时，随GFH的增大，波包谱面积增大，峰频不变，波包线的波动幅度增大，也就是说，随GFH的增大，群高有明显的差异。可见，正如所预期的，GFH与GLF分别表征波群的高度特征和长度特征。值得注意的是，尽管这2个参数的相关性不大，但如同波要素中波高和周期的关系一样，二者有一定的相关关系。依实际模拟的经验，按照式（4），即GFH值小于0.7时，GLF值取5～15，GFH值大于0.7时，GLF在10～28范围内取值，可在实验水槽中模拟出同时满足给定群高和群长要求的不规则波浪。

但需要指出的是，从图3可以看出，当GFH较小，而GLF取较大值时，波包靶谱的峰频减小，波包能量分布范围变窄，此时实测波浪的波包能量在低频段会相应的增大，同时由于高频波浪的影响［9］，在高频段实测波包能量会比目标谱值偏大，从而导致GFH计算值比目标值偏大（表1）。但是，就含主要能量的频带而言，实现的波包谱与其波包靶谱的符合程度是令人满意的。此外，为保证计算精度，特别是GLF计算值的准确性，需要强调计算中频率间隔Δf必须足够小，文中估计谱时的频率分辨率为0.003 05 Hz。

还需要指出的是，文中模拟方法虽然认为所考察的过程是非正态的，但是，在模拟方法建立的过程中近似应用了某些正态过程的理论结果。而在这个波面位移是正态分布的假定下，m0A/m0η=0.43，其中m0A和m0η分别为波包谱和频谱的零阶矩，对应地，GFH=0.74。这意味着实际正态分布的波面过程，GFH不应与0.74差别太大。例如，从表1可以看到，当给定GFH=0.4，GLF=5时，试验分析结果与目标值偏离较大。

此外，从表1统计结果可以看到，模拟所得波浪的群高越大，有效波高值越大。这是由于同样的频谱条件下，群高大的波浪其波包线的波动幅度较大，这种波浪能量分布的变化使得其有效波高值相对较大。

实验中，为考察波浪在水槽传播过程中其群性的变化，采用上述方法，在水槽x=5 m模拟所要求的波浪，在离造波机13 m、18 m和24 m处分别放置浪高仪观测波浪（图2）进而分析波浪统计特征。图6给出参数GFH和GLF随波浪传播的变化情况。可以看出，对大多实验组次，群高和群长都会沿程变化，在指定截面处表现出明显不同的群性差异，满足模拟要求。随波浪继续传播，其群性差异逐渐减小，GFH值逐渐接近。由此可知，不同于一般随机波浪的物理模型实验，在进行考虑波群的实验时，须在指定位置产生所要求群性的波浪，波浪在传播过程中，由于谐波的调制作用，波浪的群性会趋于某一有限的范围。需要指出的是，这里给出的是波浪在平底水槽传播过程中群性的变化情况，而当波浪在浅水中传播时，伴随非线性作用的增大和破碎的发生，波浪群性的变化情况及其原因为何，对此问题Mase和Iwagaki［10］以及近年来Dong和Ma［11］等进行了研究，关于这方面的探讨是文中下一步研究内容。

3 结语

应用文中建议的方法成功地实现了不规则波群的群高和群长两方面的模拟要求，模拟程序简单实用，其中波群参数GFH和GLF的取值原则是依据实际模拟的经验给出的，可供参考。在进行考虑波群的实验时，不同于一般随机波浪的物理模型实验，需在指定位置产生所要求群性的波浪。从而，实验室模拟随机波浪时在满足波高、周期相似的同时，可以作到波群相似，这对于系泊浮体和斜坡护面稳定性等方面的试验研究具有重要的意义。

［1］Funke E R，Mansard E P D.On the synthesis of realistic sea states in laboratory flume［C］//National Research Council Canada and NRC Canadian Hydraulics Centre.Proceedings of the 17th International Conference on Coastal Engineering.Sydney：ASCE，1980.

［2］XU D L，HOU W，ZhAO M，et al.The statistical simulation of wave groups［J］.Applied Ocean Research，1993，15：217-226.

［3］俞聿修，桂满海.波群的数值模拟和物理模拟［J］.大连理工大学学报，1998，38（1）：86-91.YU Y X，GUI M H.Numerical simulation and physical simulation of sea wave groups［J］.Journal of Dalian University of Technology，1998，38（1）：86-91.

［4］刘思，柳淑学，俞聿修.改进的海浪波包谱［J］.水道港口，2010，31（4）：229-235.LIU S，LIU S X，YU Y X.An improved wave envelope spectrum［J］.Journal of Waterway and Harbor，2010，31（4）：229-235.

［5］俞聿修.随机波浪及其工程应用：增订版［M］.大连：大连理工大学出版社，2000.

［6］Goda Y.A comparative review on the functional forms of directional wave spectrum［J］.Coastal Engineering，1999，41（1）：1-20.

［7］刘思，柳淑学，俞聿修，等.基于小波变换法定义的波群参数［J］.海洋学报，2010，32（2）：148-154.LIU S，LIU S X，YU Y X，et al.Wave groupiness factors defined by wavelet transform［J］.Acta Oceanologica Sinica，2010，32（2）：148-154.

［8］孙昭晨.推摇混合式造波机理论曲线［J］.中国港湾建设，1988（4）：30-32.SUN Z C.Theory curve of mixed pusher-rocker flap wavemaker［J］.China Harbour Engineering，1988（4）：30-32.

［9］Cherneva Z，Velcheva A.Wave group analysis based on phase properties［C］//MEDCOAST.Proceedings of the First International Conference on the Mediterranean Coastal Environment.Turkey：［s.n.］，1993.

［10］Mase H，Iwagaki Y.Evolution of wave groups in shallow waters and wave group properties of random waves［J］.Coastal Engineering in Japan，1987，30：19-32.

［11］DONG G H，MA Y X.Laboratory study of groupiness evolution of irregular waves on a mild slope beach by wavelet［J］.Current Development in Theory and Application of Wavelets，2009，3：81-95.