基于电磁波的低流速测量中干扰因素分析研究

杨 强 ，刘纪元 ， 焦学峰 ，么 启

（1.沈阳航空航天大学 电子信息工程学院，辽宁 沈阳 110136；2.中国科学院 声学研究所综合声纳实验室，北京 100080；3.北京航瑞博泰科技有限公司 北京 100102）

微弱信号检测一直是信号处理中的一个难题。“微弱信号”不仅意味着信号幅度很小，而且主要指的是被噪声或干扰淹没的信号。为了检测出被噪声覆盖的微弱信号，就必须分析噪声产生的原因与规律，研究被测信号的特点以及噪声的统计特性。

基于电磁波的流速测量技术是一种利用雷达多普勒原理测量流速的新技术。它是一种远距离、无接触的测量方法，适用于测量水流急、含沙量大、漂浮物多、水流复杂的一般江河的流速，具有安全、快速、使用方便等特点。但由于雷达工作中存在发射泄漏干扰和旁瓣干扰，对低流速的测量带来了困难。

1 电磁波流速测量基本原理

电磁波流速测量方法是利用雷达多普勒效应来测量流速的。雷达照射水面时，部分电磁波能量折射入水，部分能量被水面波散射，只有后向散射的那部分能量可以构成回波，波浪底下的水流基体是波浪的载体。所以波浪和基体的运动速度是相同的，接收到的信号频率相对于发射频率有一定的偏移，即波浪上的回波产生了“多普勒频偏”，它反映其水面流速，其直接关系式为：

图1 电磁波流速测量原理图Fig.1 Principle diagram of water velocity measurement by electromagnetic wave

其中：fD为多普勒频率，f0为雷达的发射频率，v为水流速度，c0为光速，α为水流的实际方向与传感器到运动目标连线之间的角度。

由式（2）可以看出，求得流速的关键是从接收信号频谱中提取多普勒频率fD。

2 雷达收发器工作原理

如图2所示，雷达收发器主要由3部分组成：信号源部分，混频输出部分和信号收发部分。具体工作原理如下。

由振荡器振荡发出一个频率为f0的发射信号，其中一路经发射天线发射出去，一路分流成两路分别进入I，Q所在通道的混频器中，其中Q通道的信号还需先经90°的移相；接收天线接收到的接收信号，先经低噪声放大处理后，再分别经混频器与实时分流的两路信号进行混频；混频后得到的信号再经中频滤波放大处理，最终得到携带有流速信息的I、Q两路中频信号，对两路信号进行分析处理，即可得到流速。

图2 雷达收发器工作原理Fig.2 Radar transceiver block diagram

3 低流速测量中干扰因素分析

低流速测量一直是电磁波流速测量中的一个难题。除了流速较低时接收信号较弱、信噪比较小不便于检测之外，发射泄漏干扰和旁瓣干扰是制约电磁波低流速测量的主要因素。

由图1电磁波流速测量的原理图可以看出，在进行流速测量时，雷达收发器的主瓣和旁瓣都会接收到多普勒频偏，分别为fD和f1D。相对于fD而言，f1D的频率会更低，从而在低频部分造成干扰，对低流速测量时造成很大影响，这种干扰称之为“旁瓣干扰”。

从图2雷达收发器工作原理可以看出，雷达接收、发射天线相距很近，由于电路中总是存在一些寄生的元件，信号与信号之间不可能做到完全隔离，总有一部分发射信号会泄漏到接收通道，这些信号和发射机发出的另一路信号相混频，差拍频率为零，即为直流。此现象称为“发射泄漏”[4]，反映到频域时会在零频附近产生很大的干扰信号，从而给低流速信号的测量造成了很大的困难[5]。

3.1 发射泄漏的影响及抑制方法

3.1.1 发射泄漏的存在主要会引起以下几个问题[5]

1）强泄漏信号会造成前置放大器饱和，因而就要接收机具有足够大的动态范围以处理目标信号和强泄漏信号。

2）发射机噪声泄漏到接收机将引起接收机灵敏度下降。任何一个连续波信号都具有噪声边带。它可以从发射机载频一直延伸到多普勒信号频率。其中一些噪声功率就落到了接收机的带宽之内。由于泄漏噪声比接收信号的功率大得多 ，所以就使得本来很容易检测的接收信号被泄漏噪声所淹没 ，引起接收机灵敏度下降。

3）由于泄漏现象的存在，会引起虚假多普勒信号的产生。

3.1.2 发射泄漏对系统的实际影响

图3即为发射泄漏对系统的实际影响，和下面的图4、5、7、8、9、11一样，横轴代表的是谱线根数，单位为频率分辨率，即Hz，图中为1 Hz，纵轴是对采集到的数字信号做FFT后的幅值，单位为V。从图3可以看出，发射泄漏信号是一个幅度很大的直流信号，反应低流速的接收信号基本被淹没在发射泄漏干扰中，且由于发射泄漏的影响，会在零频附近产生很大的干扰，对流速较低时的低频接收信号检测造成了巨大的困难。

3.1.3 发射泄露的抑制方法—去均值滤波法

去均值滤波法[6]是最经典、最常用的干扰抑制方法，常作为数据分析的预处理方法。它可以去除接收信号中的不变成分，如不变的发射泄漏干扰和电路产生的热噪声等。它的基本思想是：采集到的一组回波数据中，发射泄漏干扰可以认为是固定不变的，它近似等于该组数据的平均值，因此我可以用去均值滤波的方法来消除。

图3 发射泄露干扰的影响Fig.3 Inference of transmit leakage

去均值滤波法非常简单，但对于消除接收信号中的发射泄漏干扰效果很好，因此把它作为回波数据分析中的预处理方法。

图4为去均值滤波法运用到图3中信号后的时频域波形图。从图4可以看出，去均值滤波可以很好地消除发射泄漏干扰的影响。

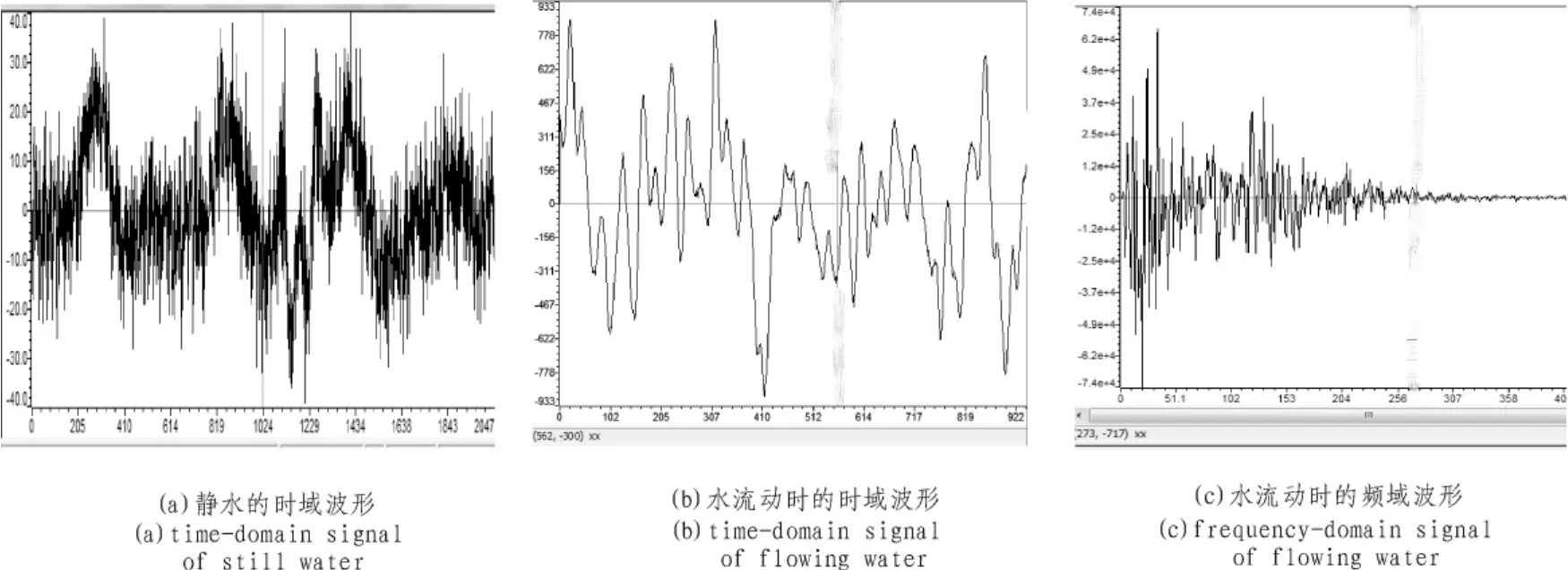
图4 去均值滤波Fig.4 Mean filter

3.2 旁瓣干扰的影响及抑制方法

3.2.1 旁瓣干扰会带来的问题[7]

均匀分布的雷达天线波束的旁瓣位置取决于（4）式：

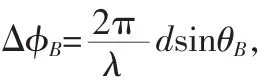
由图1可以看出，由于雷达多普勒效应，雷达主瓣和旁瓣分别接收到带有速度信息的多普勒频偏fd和f1d，

由式（8）得f1d要比fd小得多。虽然雷达旁瓣信号发射功率相对于主瓣信号会有13.4 dB[式（7）]的衰减，但由于旁瓣距离水面的距离更近，相比于主瓣，能量衰减更小，再加上主瓣散射信号的叠加效应，实际上旁瓣信号相对于主瓣信号的衰减会远远小于13.4 dB，因此会在低频部分产生很强的干扰信号。当流速较低，接收信号较弱时，旁瓣的干扰影响会更加明显。

3.2.2 旁瓣干扰对系统的实际影响

由图5（a）可以看出，由于旁瓣的干扰造成了主瓣信号关于中心频率的不对称，由图5（b）可以看出，旁瓣干扰在低频部分影响很大，对低流速测量带来了很大的困难。

3.2.3 旁瓣干扰的抑制方法

由于水面流速的不稳定，电磁波照射到水面时，散射回来的接收信号中多普勒频率是一个频率带，如图5所示，其中每条功率谱线对应着一个速度值。为了得到真实接收信号的平均值，滤除噪声和旁瓣干扰，设计时采用了频域带通滤波的方法。

图5 旁瓣干扰的影响Fig.5 Side-lobe interference

与以往的带通滤波器不同，这里设计的带通滤波器是在计算得到接收信号的频谱特性之后，在频域内进行加窗处理，然后只对窗内的频率成分进行分析计算，从而实现带通滤波。具体流程图如图6所示。

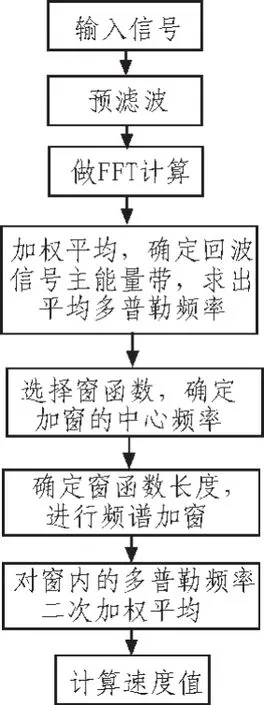
图6 频域带通滤波流程图Fig.6 Flow chart of band-pass filter infrequency domain

设雷达接收到的第n组数据记为An=[an1，an2，…anm]，对应频率为 Fn=[fn1，fn2，…fnm]，幅度为 Dn=[dn1，dn2，…dnm]，m 为数据长度。则频域带通滤波的具体算法过程可归纳为以下5个步骤：

1）预滤波算法

这里采用的预滤波算法就是前面3.1.3节中提到的去均值滤波法，把接收信号中的发射泄漏干扰消除掉，从而方便后面的信号分析处理。

2）加权平均算法

为了减少计算量，笔者提出了阈值抽取加权平均来计算平均频率。即设定一个幅度阈值Ddor（一般为最大噪声谱对应幅度的10倍左右），在全频域内，只对幅度超过阈值的多普勒频率加权平均，从而大大减少了计算量。

图7中（a）为输入信号为30~50 Hz的扫描频率频域波形和用阈值抽取加权平均计算得到的多普勒平均频率。图中代表加权平均后得到的频率计算值，单位为Hz。从图中可以看出，计算值与理论值是一致的。

图7 单次阈值抽取加权平均法Fig.7 Single weighted average

单次阈值抽取加权平均方法减小了运算量，但是不能修正旁瓣干扰带来的低频成分对多普勒频率造成的低频偏移，如图7（b）所示，其中（b）为（a）中信号掺杂了低频分量之后的频域波形和加权平均之后计算得到的多普勒平均频率。从图中看出，在输入信号为30~50Hz的扫描频率中掺杂一个较大的低频干扰时，计算得到的多普勒平均频率为31 Hz，即产生了多普勒频率的低频偏移。为了解决这个问题，提出了频谱加窗之后进行二次加权平均的方法。

3）窗函数的选择

数字信号处理中常用的窗函数主要有矩形窗（Rectangular）、三角窗（Triangular）、汉宁窗（Hanning）、海明窗（Hamming）、布莱克曼窗（Blackman）和凯泽窗（Kaiser）等。图8是常见的几种窗函数在不同点数时的时域波形。

从图8中可以看出点数一定时，布莱克曼窗函数的主瓣是最窄的，下降速度也是最快的，因此选用布莱克曼窗函数来实现频谱加窗。

4）确定中心频率，进行频谱加窗

频谱加窗的难点在于找到功率谱的解析式，在这里首先采用单次阈值抽取加权平均的方法来确定接收信号的主能量带和多普勒平均频率。由于已知低频偏移的存在，在大于的N点内搜索一个最大值Dmax，然后计算以Dmax为中心左右N点内的平均频率，并把作为中心频率进行频谱加窗。其中N的大小是根据的大小来确定的。

5）二次加权平均

实现频谱加窗之后，在窗内进行二次加权平均，将计算得到的平均值作为接收信号的最终多普勒平均频率，从而进行速度值的计算。

图8 几种常见的窗函数Fig.8 Several common window functions

3.2.4 仿真分析

图9 中（a）即为图5 中（b）波形，图9 中（b）为（a）频谱加窗之后的频域波形，（c）中从为单次阈值抽取加权计算得到的多普勒平均频率，为频谱加窗之前搜索到幅度谱最大的多普勒频率，为频域带通滤波之后计算得到的多普勒平均频率。从图9可以看出，在掺杂了低频分量之后，单次加权平均找到的多普勒平均频率产生了低频偏移，而经过频谱加窗和二次加权平均构造的频域带通滤波之后则很好地修正了这一问题，从而可以很好地抑制旁瓣干扰。

图9 频域带通滤波Fig.9 Band-pass filter in frequency domain

3.3 实验验证

笔者采用的实验测试系统是由浮子式流量计和一个标准段水渠组成。当水泵开启，水流动起来时，流量计指示流量为20 m3/h，此时水深为 0.205 cm，渠道宽0.17 cm，由此可得速度为0.159 4 cm/s。

图10是实验所得的测量值，图中（a）为接收信号经过预滤波消除发射泄漏的频域波形，（b）为加窗处理后的波形，（c）中为单次阈值抽取加权计算得到的多普勒平均频率，为频域带通滤波之后计算得到的多普勒平均频率，为计算得到的速度值，单位为cm/s。从测量值看来，经预滤波去除发射泄漏之后的接收信号，经带通滤波后得到的速度值会更接近真实值，很好地抑制旁瓣干扰带来的低频偏移，从而解决了低流速测量中的困难。

图10 频域带通滤波在实际测量中的应用Fig.10 Application of band-pass filter

4 结 论

低流速测量由于信噪比低，干扰信号强，一直是电磁波流速测量中的难题。从电磁波流速测量的基本原理出发，分析了发射泄漏干扰和旁瓣干扰对低流速测量的影响。针对两种干扰的信号特性，分别提出了取均值滤波及频域带通滤波的方法来抑制干扰。通过仿真分析和实验验证，运用这些方法可以很好的抑制干扰信号，但无法消除干扰。经过反复实验，当水流速度大于10 cm/s时，系统运行可靠稳定，当水流速度在10 cm/s以下时，系统运行并不稳定。因此，将速度小于10 cm/s以下的极小水速为系统的盲区不予测量。

[1]高晋占.微弱信号检测[M].北京：清华大学出版社，2002.

[2]张建海.LD15-1型电波流速仪的比测与应用 [J].水利水文自动化，1997（3）：13-17.

ZHANG Jian-hai.Measurements and applications of LD15-1-type electromagnetic flow meter [J].Automation in Water Resources and Hydrolog，1997（3）：13-17.

[3]丁鹭飞，耿富录，陈建春.雷达原理[M].北京：电子工业出版社，2009.

[4]龚克，范春凤，刘百超.零中频接收机及其直流偏移抑制方法[J].周口师范学院学报，2008，25（2）：52-54.

GONG Ke，FAN Chun-feng，LIU Bai-chao.Zero-IF receiver and suppression methods for DC-offset[J].Journal of Zhoukou Normal University， 2008，25（2）：52-54.

[5]周永辉.连续波雷达发射泄漏抑制技术研究[D].南京：南京理工大学，2004.

[6]李廷军.探地雷达干扰抑制及波速估计问题的研究[D].成都：电子科技大学，2009.

[7]张光义.相控阵雷达系统[M].北京：国防工业出版社，2001.

[8]张贤达.现代信号处理[M].北京：清华大学出版社，2002.

[9]刘波，文忠，曾涯，等.MATLAB信号处理[M].北京：电子工业出版社，2006.