基于LabVIEW仿真实现TSP问题的模拟退火算法

赵敬和，谢 玲

（1.中国地质大学 地球物理与信息技术学院，北京 100083；2.青岛理工大学 自动化工程学院，山东 青岛 266033）

TSP问题[1]是图论研究中的一个经典算法问题，皆在寻找各个城市结点之间的最短路径。问题的主要种类有：确定起点的TSP问题；确定终点的TSP问题；全局最优的TSP问题。其中TSP问题是求连接各个城市之间最短路径，它的限制条件最少，但答案的可能性最多。TSP问题在实际应用中具有典型意义，如可用来解决分配问题、路径问题、车辆调度问题、网络问题、切割问题等。

模拟退火算法[1]（SimulatedAnnealing，SA）最早由 Kirkpatrick等应用于组合优化领域，它是基于Mente-Carlo迭代求解策略的一种随机寻优算法。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能，具有很强的全局搜索能力、通用性强、鲁棒性高，目前已在工程中得到了广泛应用，诸如函数优化、生产调度、图像处理、控制工程、机器学习、神经网络、信号处理、人工智能与科学计算等领域。Workench）是开发虚拟仪器的集成环境，是美国国家仪器（NI）公司的创新软件产品，也是目前应用最广、发展最快、功能最强的图形化软件集成开发环境，主要用于开发测试、测量与控制系统。所有的LabVIEW应用程序，即虚拟仪器，包括前面板、流程图（后面板）以及图标/连接器3部分。

传统的文本代码式编程语言是控制流程图，程序是按语句的先后顺序来执行的；而LabVIEW图形化编程是数据流编程，只是要当某个节点的输入数据都变为有效时，节点就开始运行。

LabVIEW程序采用模块化方法，它由各个模块组成，每个模块实现特定的功能，将它们组合起来之后就可以开发出一个大的用户程序或项目。子VI作为LabVIEW编程的层次化和模块化编程的重要组成部分，子VI的使用可以让整个程序结构变得更加清晰、层次更加分明、程序更加易读和维护。

1 LabVIEW的介绍

2 模拟退火算法（Simulated Annealing）

LabVIEW[2]（Laboratory Virtual Instrument Engineering

2.1 模拟退火算法概述

模拟退火又称MonteCarlo退火，是一种常用的全局优化方法，它来源于固体退火原理：将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状态，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

模拟退火算法（SA）是一种新的随机搜索方法，是近年来提出的一种适合于解决大规模组合优化问题的通用而有效的近似算法。与其它搜索方法相比，具有如下的特点：以一定的概率接受恶化解；引进算法控制参数；使用对象函数值进行搜索；搜索复杂区域；具有描述简单、使用灵活、运用广泛、运行效率高和较少受到初始条件约束等优点。

2.2 模拟退火算法原理

模拟退火算法（AS）源于统计物理学，是模拟熔化状态下物体由逐渐冷却至最终达到结晶状态的物理过程。模拟退火算法是利用问题的求解过程与熔化物体退火过程的相似性，采用随机模拟物体退火过程来完成问题的求解，也就是在控制参数（温度）的作用下对参数的值进行调整，直到所选取的参数值最终使能量函数达到全局极小值。

1982年，Kirkpatrick等将退火思想引入组合优化问题，同时综合了统计物理学和局部搜索方法，提出一种解大规模组合优化问题的方法，特别是NP完全组合优化问题的有效近似算法～模拟退火算法。采用Metropolis接受准则，并用一组称为冷却进度表的参数控制算法进程，使算法在多项式时间里给出一个近似最优。Metropolis准则是Metropolis等1953年提出的重要性采样法。

算法计算过程为[3-4]：

1）初始化：初始温度T0，初始解状态S（是算法迭代的起点），每个温度值的迭代次数L，温度衰减系数α，令当前温度T=T0，终止条件 q；

2）在当前温度下，对 k=1，2，……，L 做第 3） 至第 6）步；

3）产生新解 S′；

4）计算增量 ΔC′=C（S′）-C（S），其中 C（S）为评价函数；

5）若 ΔC′＜0，则接受 S′作为新的当前解，否则以概率

exp（ΔC′/T）接受 S′作为新的当前解；

6）如果满足终止条件则输出当前解S′作为最优解，结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法；

7）T=αT 逐渐减少，且 T＞0，然后转第 2）步。

按照一定的退火方案逐步降低温度，重复Metropolis过程，当系统温度足够低时，可认为达到了全局最优化状态。

3 旅行商问题的定义与模型

TSP问题从问题描述上来看是一个非常简单的问题，它指的是一个旅行者想周游多个城市，条件是必须每个城市都要访问到，并且只能访问一次，然后返回出发城市。在给定城市间的旅行距离的前提下，要求在完成对所有城市的访问后，所走的距离最短。即：

假设有一个图G=（V，E），其中V是定点集，E是边集，设D=dij是顶点i和j之间的距离所组成的距离矩阵，旅行商问题就是求出一条通过所有顶点且每个顶点只通过一次的具有最短距离的回路。若旅行商要访问的城市数量为n个，那么访问所有城市路径的组合数量就有（n-1）!个。这里当n的数值不大时，我们很容易找到整个访问过程的最短路径。但是，当n的数值非常大时，整个访问路径的组合数量就会急剧的增加，最后达到人工无法计算程度。

4 模拟退火算法TSP问题的LabVIEW仿真

模拟退火算法解决 TSP问题：问题重述，已知这个城市之间的相互间距离，现有一个旅行者必须访遍这n个城市，并且每个城市只能访问一次，最后又必须返回出发城市。

在此由8个LabVIEW的子VI模块实现模拟退火算法解决该TSP问题的求解。首先，建立产生1到n（n表示城市数，在此城市分别给以标号）数组、产生随机路径、任意两城市间距离、任意路径的距离、两组路径选优程子VI，然后是主程序选模拟退火算法的优化过程、画图子VI，最后是主界面的子VI[5]。

主程序模拟退火算法实现流程如图1所示。

图1 主程序算法的程序流程图Fig.1 The flow chart of main program algorithm procedures

主界面实现模拟退火算法的初始条件：初始温度、结束温度的设置、城市距离文件的读取，以及结果的查看（分图形化和数字化，图形化是可以直接查看走的路径和线路，数字化就是以城市的标号，直观地表示出路径），其主界面的流程图如图2所示。

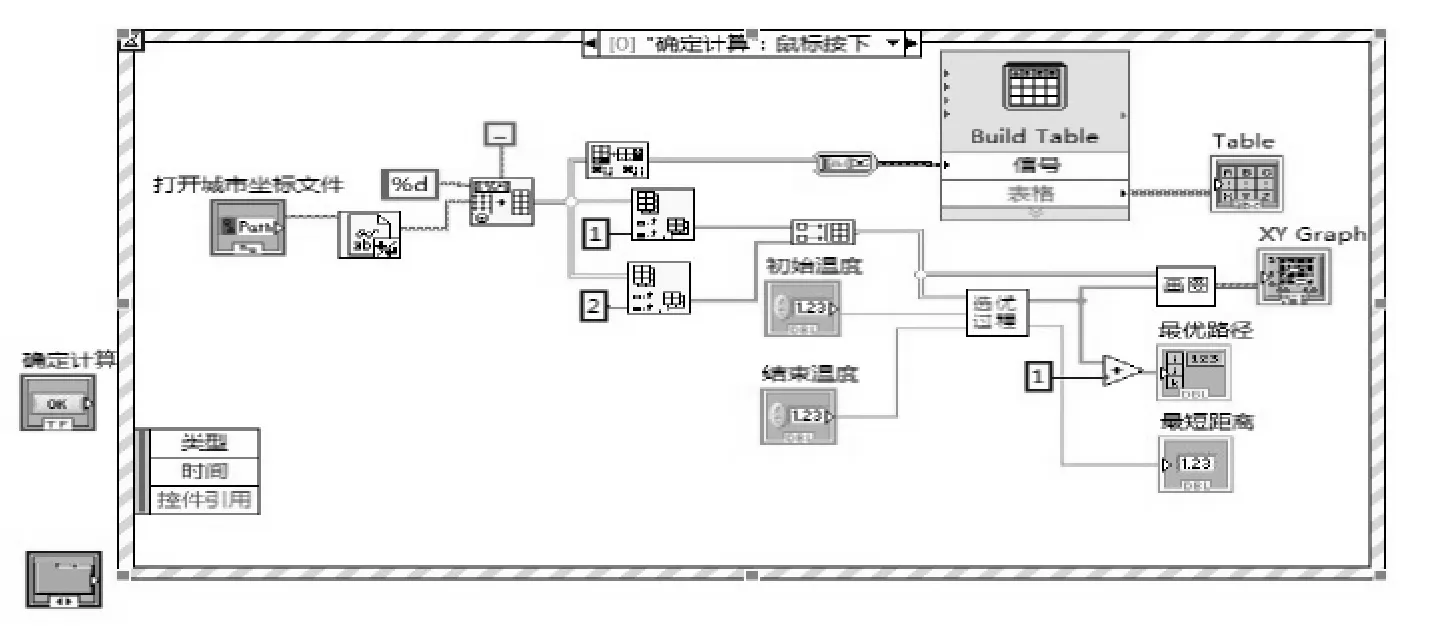
图2 主界面的程序流程图Fig.2 Program flow chart of main interface

文中选取31个省会城市作为测试样本，其相对坐标为cities=[1 304，2 312；3 639，1 315；4 177，2 244；3 712，1 399；3 488，1 535；3 326，1 556；3 238，1 229；4 196，1 004；4 312，790；4 386，570；3 007，1 970；2 562，1 756；2 788，1 491；2 381，1 676；1 332，695；3 715，1 678；3 918，2 179；4 061，2 370；3 780，2 212；3 676，2 578；4 029，2 838；4 263，2 931；3 429，1 908；3 507，2 367；3 394，2 643；3 439，3 201；2 935，3 240；3 140，3 550；2 545，2 357；2 778，2 826；2 370，2 975；]， 由LabVIEW仿真实现模拟退火算法对TSP问题的计算结果（也即主界面图）如图3所示。

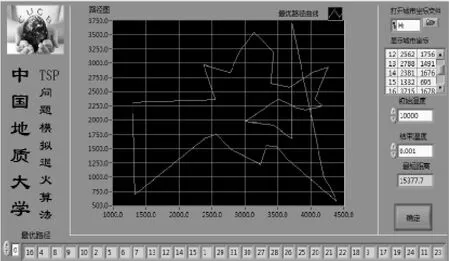
图3 LabVIEW计算结果的路径图Fig.3 The path chart of LabVIEW calculation results

以上两图是针对31个城市坐标的TSP问题程序进行的仿真，在初始温度10 000，结束温度0.001，温度衰减系数为α=0.95情况下，计算得到的31个城市间最短往返距离是15 377.7 km. 城市的访问次序为：16、4、8、9、10、2、5、6、7、13、12、14、15、1、29、31、30、27、28、26、25、20、21、22、18、3、17、19、24、11、23。

运用LabVIEW软件实现的解决TSP问题的模拟退火算法，计算多次虽然城市的访问起点不同，但城市的访问次序是一定的，说明该LabVIEW实现的模拟退火算法的仿真将结果具有稳定性，以及算法的可靠性。

5 结果分析

对于同样的TSP问题用matlab编程来实现其模拟退火算法解，在此应用相同的城市数据，经多次计算，最优结果15 461 km，路径如图4所示。

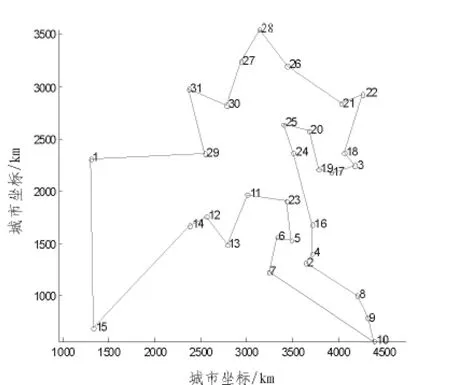
图4 matlab计算结果的路径图Fig.4 The path chart of matlab calculation results

还有与文献[6]中的最优结果15 383 km对比（在文献[6]中有详细的路径图），LabVIEW实现的结果明显占有优势，比其它的软件实现的结果要好。

显然LabVIEW实现模拟退火算法对同样的TSP问题计算得出的结果要优。

6 结束语

本文主要针对LabVIEW做了简单的介绍，对模拟退火算法原理进行了分析，完全由LabVIEW来实现该算法的计算过程，并将该算法应用于TSP问题的求解，得到了预期效果。前人有很多用遗传算法求解该TSP问题，但结果也不是非常的理想，但是如果用LabVIEW把这两种算法结合起来一起实现，可能结果会更好，因此还有许多工作有待研究，需进一步去实现。

[1]康立山，谢云.非数值并行算法-模拟退火算法[M].北京：科学出版社，1994.

[2]雷振山，赵晨光，魏丽，等.LabVIEW8.2基础教程[M].北京：中国铁道出版社，2008.

[3]曲晓丽，潘昊，柳尚斌.旅行商问题的一种模拟退火算法求解[J].现代电子技术，2007（18）：78-82.

QU Xiao-li，PAN Hao，LIU Shang-bin.Solution of travelling salesman problem by a kind of simulated annealing algorithm[J].Modern Electronics Technique，2007（18）：78-82.

[4]郭茂祖，洪家荣.基于模拟退火算法旅行商问题的并行实现[J].哈尔滨理工大学学报，1997（5）：80-83.

GUO Mao-zu，HONG Jia-rong.A parallel algorithm for the simulated annealing based traveling salesman problem[J].Journal of Harbin University of Science and Technology，1997（5）：80-83.

[5]杨多星，刘蕴红.基于LabVIEW仿真的全局最短路径的遗传算法[J].电子设计工程，2010（10）：29-33.

YANG Duo-xing，LIU Yun-hong.Genetic algorithm design of the global shortest path lines based on LabVIEW simulation[J].Electronic Design Engineering，2010（10）：29-33.

[6]高尚.求旅行商问题的模拟退火算法[J].华东船舶工业学院学报：自然科学版，2003，17（3）：13-16.

GAO Shang.Sloving TSP with simulated annealing algorithm[J].Journal of East China Shipbuilding Institute：Natural Science，2003，17（3）：13-16.