海上风电基础结构疲劳寿命分析

李 炜，李华军，郑永明，周 永

(1.中国水电顾问集团华东勘测设计研究院，浙江 杭州 310014;2.中国海洋大学，山东 青岛 266100)

对于海上结构物而言，风、浪、流等环境荷载交互作用引起疲劳失效是影响其安全性的重要因素.例如亚历山大·基尔兰号半潜式生活平台的失事，就是首先从平台一根撑杆发生疲劳断裂开始的.交变荷载下的结构破坏通常从节点开始，因此有必要对结构物节点位置进行疲劳寿命分析.

海上风电基础结构的稳定性及抗疲劳特性直接影响到风电结构整体稳定性和疲劳寿命，API和DNV等规范中也给出了推荐方法或相关建议［1－2］，其中，需指出的是API规范中提供的波浪作用下疲劳校核的简化方法是一种近似方法，其在海上风电基础结构疲劳分析中的适用性有待于通过详细的疲劳分析数据进行校准，这需要大量详细疲劳校核工作的积累.因此，针对海上风电基础结构的静、动力分析及疲劳寿命评测等方面的研究是非常必要的［3－12］.

本文重点针对基础结构疲劳特性评测、疲劳寿命评估展开，以三桩基础结构型式为例，采用基于Miner线性累积损伤法则的疲劳寿命评价方法计算了其线性累积损伤及疲劳寿命;区分疲劳荷载为单级疲劳荷载和多级疲劳荷载联合作用两种情况，考虑疲劳荷载的3种作用方式(渐增型、往复型、正弦波型)时，结构的疲劳特性和疲劳寿命，以S-N曲线所体现的结构疲劳极限对应的应力水平为参照，定义疲劳极限与疲劳荷载作用下结构各部位应力水平的比值为安全系数，并以其云图直观地对结构在疲劳荷载作用下各个部位的抗疲劳能力进行量化评估.

以安全系数量化结构不同部位的抗疲劳性能，需要先得到荷载作用下结构不同位置的应力信息，即数值模拟中对结构进行网格划分得到的单元或节点的应力信息，而应力信息是根据疲劳荷载的施加得到的，本项研究中，对于多级疲劳荷载情况以两个方向施加疲劳荷载对比计算效果，即疲劳荷载“低→高”(下文称为WAY1)和“高→低”(下文称为WAY2)，以分析疲劳荷载对于基础结构的“锻炼效应”.

1 Miner理论基本原理

疲劳是结构失效的常见原因，与重复加载相关.疲劳寿命是结构受力直至破坏所作用的荷载循环次数或时间.循环荷载又称交变荷载，可以分为常(恒)幅荷载和变幅荷载，是最为简单的疲劳荷载形式.典型的交变应力－时间的变化历程如图1所示.其中:σmax和σmin分别为最大和最小应力;σa=(σmax－σmin)/2为应力幅，是反映交变应力大小的指标;σm=(σmax+σmin)/2为平均应力;Δσ=σmax－σmin=2σa为应力范围.

针对疲劳荷载的作用形式，将其区分为以下3种(见图2):(1)渐增型，即荷载F按照从0到1的线性渐增模式加载至疲劳荷载Fmax(下文以“MODE_1”表示);(2)往复型，即荷载以相对方向往复激振作用方式施加(下文以“MODE_2”表示);(3)正弦波型，即荷载以正弦波的方式作用(下文以“MODE_3”表示).对于疲劳荷载类型，本文将其区分为单级疲劳荷载和多级疲劳荷载两种形式.

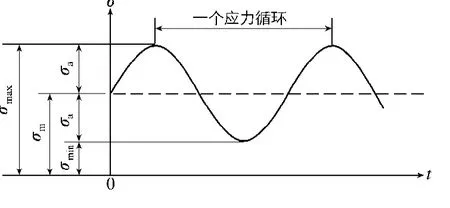
图1 交变应力时间历程Fig.1 Alterlating stress-time history

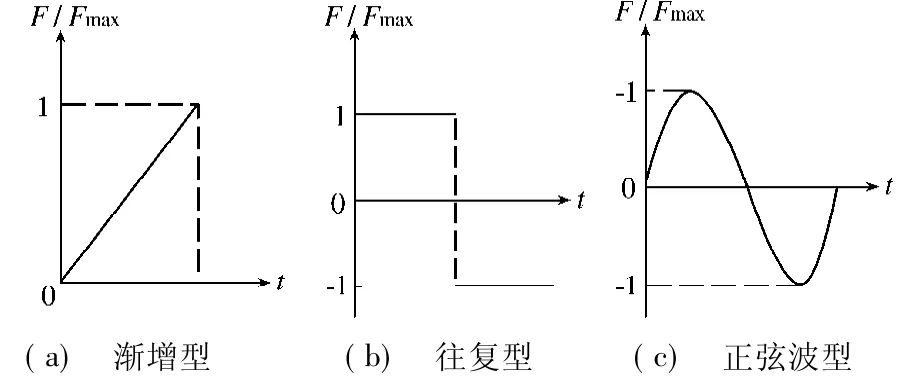
图2 加载方式Fig.2 Loading modes

本质上，S-N曲线法仅适用于预报裂纹的起始寿命，但由于通常情况下都是人为定义“破坏”，因此疲劳破坏的概念被模糊化，原来的扩展过程被简化为一个状态，从而也将S-N曲线法用于估计结构的全寿命期.

对于多数海洋工程结构物而言，所承受的循环荷载是随机变化的，因此需要借助疲劳累积损伤准则，工程中常用的是线性疲劳累积损伤理论中较为典型的Palmgren-Miner理论(简称Miner理论).线性疲劳累积损伤认为结构在循环荷载作用下的疲劳损伤是线性累积的，且当累积达到一定程度时，结构发生疲劳破坏.结构遭受等幅、变幅荷载作用下的累积损伤可以分别表示为，其中n为循环次数;N为对应于常幅荷载的疲劳寿命;ni，Ni分别为对应于变幅荷载Fi的循环次数和疲劳寿命;Miner理论的累积损伤破坏准则为

海洋平台管结点疲劳破坏的显著特点是低周疲劳破坏［9］，即每个荷载循环的前半周和后半周，结构的同一部位发生方向相反的塑性流动，循环结束后总塑性应变几乎为零，随着塑性损伤的不断累积，经过有限次的循环，开始形成疲劳裂纹，进而逐步扩展直至贯穿整个断面以致断裂.管节点的疲劳寿命主要取决于交变应力作用下形成的塑性区塑性应变的大小，因此，进行细致的疲劳寿命分析，首先要弄清管节点应力分布.

Miner理论的缺陷没有考虑加载顺序的影响，它用以评价或计算损伤的应力水平是独立的;而加载顺序对于结构疲劳寿命的影响非常大，简单而言，从高到低与从低到高对结构施加同一组疲劳荷载，所造成的疲劳损伤存在很大差异.鉴于此，本文区分疲劳荷载加载顺序为由高到低和由低到高两种形式，对此类影响进行了分析.

2 算例

假设某海上风电基础结构为图3所示的三桩型式:塔筒2.7～4.5 m变径，斜撑2.0～2.7 m变径;泥面水平撑1.4～1.6 m变径.疲劳分析中所用S-N曲线参考文献［1］.

图3 基础结构Fig.3 Foundation structure

疲劳计算需依据每级疲劳载荷作用下结构的应力水平展开，常规方法是采用管单元以杆系简化建模方式模拟.此时，图3结构共有5个“节点”，即3个斜撑与塔筒交接处(1个)，斜撑与桩套管连接处(3个)，水平撑与塔筒连接处(1个).因管单元计算的应力往往偏小，故本文采用壳单元模型建模，这样应力计算结果更为合理，且原来每个“节点”均被细化，可更直观和细致地观察损伤位置，并根据损伤位置或部位对结构细部进行加强.

风机厂家对于荷载的提供往往以基础顶法兰处(与上部风机结构连接处)为参照，疲劳荷载也是如此，即施加在基础顶的法兰处.算例主要研究内容如下:

(1)单级疲劳荷载作用 包括结构线性累积疲劳损伤;MODE_1～3的3种荷载作用方式对疲劳损伤计算的影响;以安全系数云图量化结构不同部位抗疲劳能力.

(2)多级疲劳荷载联合作用 与单级疲劳荷载作用下的研究内容相同，将荷载类型改为多级疲劳荷载联合作用.其中，安全系数定义为疲劳极限与疲劳荷载作用下结构相关部位应力水平的比值，并以云图形式显示0.5～2.0范围内的安全系数，例如安全系数为1.2则表示疲劳极限为当前疲劳荷载造成的应力水平的1.2 倍.

(3)瞬态动力学分析 假定结构受到图4所示的冲击荷载和激振荷载作用(x方向)，对结构整体进行瞬态动力学分析.

图4 时程曲线Fig.4 Time history

3 计算结果分析

3.1 单级疲劳荷载作用

假设基础结构受某单级疲劳荷载作用:水平力Fx=275 kN;弯矩M=24 810 kN·m;扭矩T=3 900 kN·m，循环1×107次.对结构数值模拟中出现最大应力的节点node44处进行重点分析，经过计算，疲劳荷载造成结构该部位疲劳损伤为3.571×10－2，则可得结构寿命约28 a.

以MODE_1～3的3种形式加载，结构最小安全系数(Fs，min)分别为大于2，1.741和1.459，可见对于3种加载方式而言，按照造成疲劳损坏的恶劣程度排序:正弦波＞往复型＞渐增型.

(1)MODE_1加载 经计算，该加载方式情况下安全系数均大于2，在所观察的0.5～2.0范围的安全系数云图不会有相应的显示，为查看薄弱部位，将疲劳荷载造成的应力水平放大观察，这里放大5倍(Scale=5)，安全系数如图5所示.

(2)MODE_2加载 该加载方式情况下，结构安全系数如图6所示，其中图6(a)未经放大，图6(b)取Scale=5以便与MODE_1进行同水平比较.

(3)MODE_3加载 该加载方式情况下，结构安全系数如图7所示，其中图7(a)未经放大，图7(b)亦取Scale=5以便与MODE_1和MODE_2进行同水平比较.

由图5～7可见:斜撑与塔筒及桩套管连接处是疲劳破坏的易发区;同时，从安全系数云图可以直观地对结构各部位的抗疲劳能力做出观察和评判.另外，从云图中的安全系数云图区域亦可看出，3种加载方式造成损伤的严重程度是正弦波＞往复型＞渐增型.

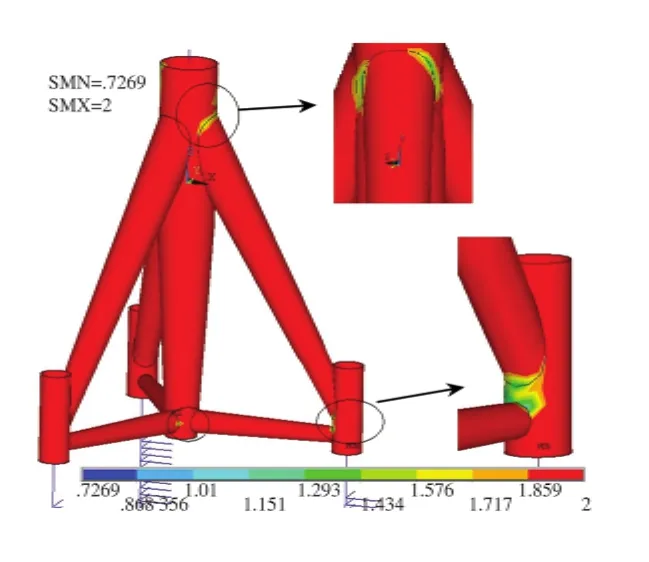
图5 MODE_1安全系数(放大5倍)Fig.5 Fatigue safety factor for MODE_1(scale=5)

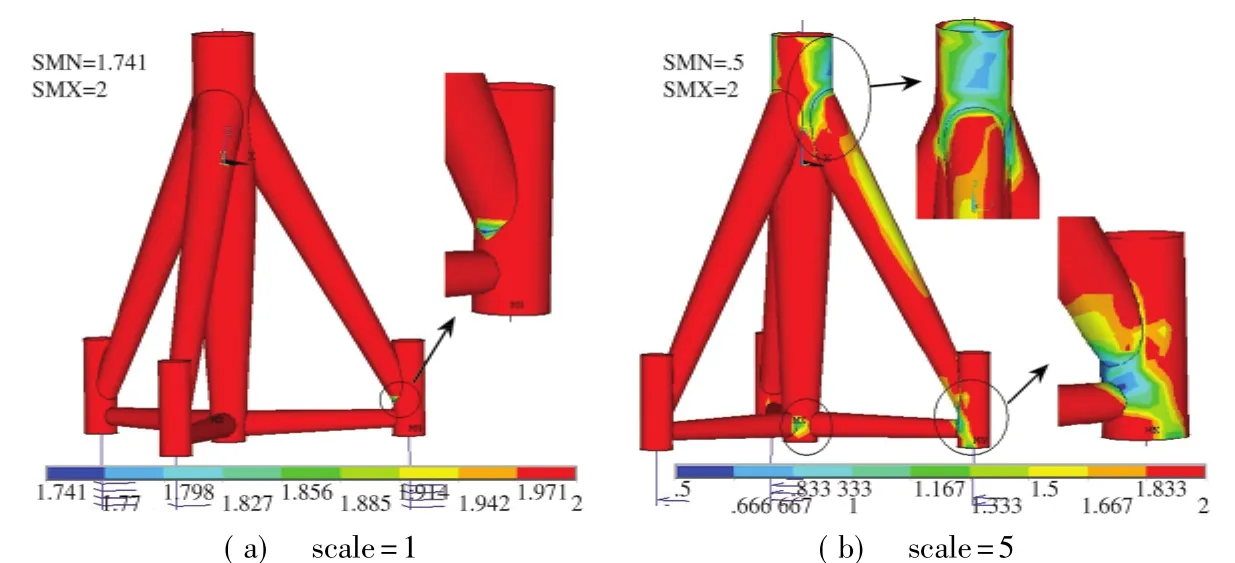
图6 MODE_2安全系数Fig.6 Fatigue safety factor for MODE_2

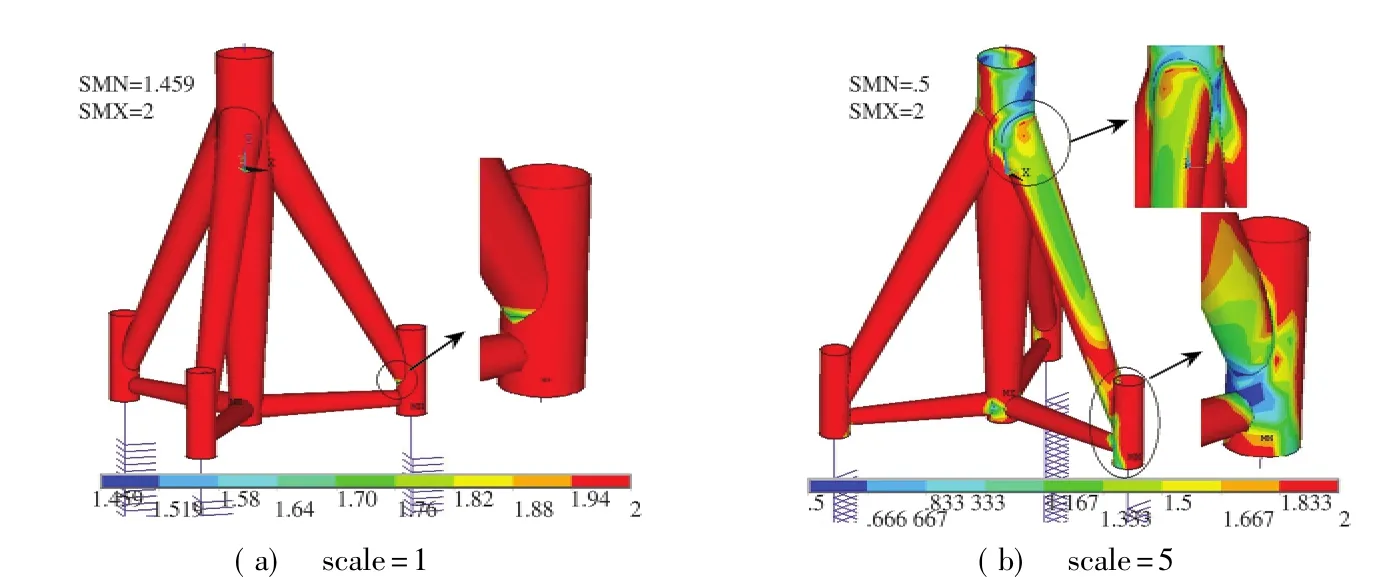
图7 MODE_3安全系数Fig.7 Fatigue safety factor for MODE_3

3.2 多级疲劳荷载作用

假设基础结构受到表1所示的11级疲劳荷载作用.疲劳寿命及相应的疲劳损伤计算结果列于表1.根据Miner理论，可求得结构线性累计损伤为0.032考虑，一定的安全系数，如3，得到结构在给定的疲劳荷载作用下累计损伤为0.096，小于1，满足要求.

表1 疲劳荷载Tab.1 Fatigue loads

Miner理论认为各级疲劳荷载之间相互独立，其计算模式是分别单独求解各级疲劳荷载作用下的结构疲劳损伤，最后累积叠加各损伤值作为结构总体累积损伤，因此无法体现加载顺序的影响，而实际工程中，加载顺序对结构的疲劳损伤影响是不容忽视的.为了解加载顺序的影响，本文借助有限元软件的时间步加载模式，将各级疲劳荷载按照“低→高”(WAY1)和“高→低”(WAY2)的顺序加载，获取结构应力水平信息，并按照MODE_1～3的3种表现模式分别分析该应力水平，得到结构安全系数量化云图见图8所示，其中图8(b)表示WAY2应力水平放大5倍.

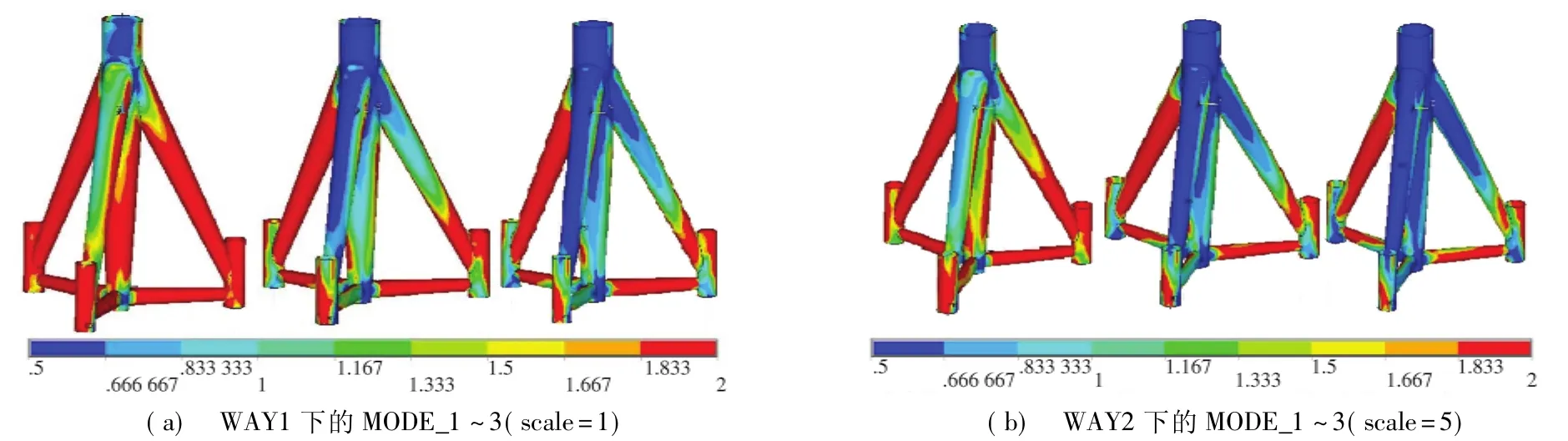
图8 安全系数Fig.8 Fatigue safety factor

可见，3种作用方式造成结构疲劳损伤的能力依然体现为:正弦波＞往复型＞渐增型;对于同样的多级疲劳荷载和同样的加载方式而言，疲劳荷载由高到低的作用顺序对于结构抗疲劳能力是不利的，即由低到高加载顺序对于结构产生“锻炼效应”.

图9 x方向位移响应(冲击荷载)Fig.9 x-displacement response

3.3 瞬态动力学分析

在图4(a)冲击荷载作用下，沿高程递增(node 1～4)摘取塔筒上4个点，其中node 4位于塔筒顶部，x方向位移响应见图9.

可见，距离冲击点较近的node1点位移响应峰值与冲击荷载开始作用的t=2 s时刻接近，随着高程的增加，塔筒高处远离冲击点的位置所出现的位移响应峰值逐渐滞后于t=2 s时刻;沿塔筒方向，随着高程的增加，x方向位移响应峰值渐增，响应曲线摆动幅度愈发明晰，换言之，距离冲击点较近的位置，响应峰值滞后会伴随冲击荷载的渐减而渐趋平稳，而距离冲击点较远的塔筒高处位置在位移响应峰值之后，尽管也呈衰减趋势，但在惯性力作用下，趋于平缓所需的时间较长.

冲击荷载作用下，结构疲劳损伤识别结果可通过图10(a)所示的安全系数云图及换算为概率统计结果的云图显示.其中，概率统计结果表示失效概率百分比.

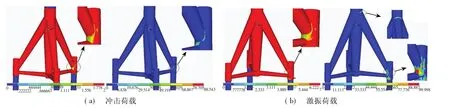
图10 安全性识别Fig.10 Safety identification

可见，在该冲击荷载作用下，结构易发生疲劳破坏的部位是斜撑与桩套管连接处.在图4(b)激振荷载作用下，结构疲劳损伤识别结果可通过图10(b)所示.可见，斜撑与塔筒连接处、斜撑与桩套管连接处均为易出现疲劳区域.

4 结语

研究了海上风电基础结构疲劳分析方法，区分荷载类型为单级疲劳荷载和多级疲劳荷载，依据线性累积损伤理论对结构疲劳损伤及疲劳寿命进行了计算;选用渐增型、往复型、正弦波型这3种疲劳荷载作用方式研究了疲劳荷载作用方式对结构疲劳损伤的影响，验证了疲劳荷载作用方式对结构疲劳损伤的影响不容忽视，并以安全系数量化结构不同区域抗疲劳损伤的能力.

在本研究所涉及的基础结构型式、疲劳荷载取值情况下，3种作用方式造成的结构疲劳损伤严重程度为渐增型＜往复型＜正弦波型.

通过对比加载顺序对结构疲劳损伤的影响，说明线性累积损伤理论无法考虑加载顺序影响.

［1］API RP 2A-WSD(2007)，Recommended practice for planning，designing and constructing fixed offshore platforms-working stress design［S］.

［2］DNV-OS-J101(2010)，Design of offshore wind turbine structures［S］.

［3］李炜，郑永明，周永.近海风电基础桩土作用3D有限元模拟［J］.水电能源科学，2010，28(8):162-164.(LI Wei，ZHENG Yong-ming，ZHOU Yong.3D-FEM simulation of soil pile interaction for offshore wind power generation［J］.Water Resources and Power，2010，28(8):162-164.(in Chinese))

［4］李炜，郑永明，周永.海上风电基础ANSYS数值模拟［J］.水运工程，2010(8):125-128.(LI Wei，ZHENG Yong-ming，ZHOU Yong.Computer simulation of offshore wind turbine using ANSYS［J］.Port＆ Waterway Engineering，2010(8):125-128.(in Chinese))

［5］LI Wei.Study on the fuzziness in fatigue life estimation of the foundation of offshore wind turbine［J］.Advanced Materials Research，2011，243-249:4741-4745.

［6］李茜，杨树耕.采用ANSYS程序的自升式平台结构有限元动力分析［J］.中国海洋平台，2003，18(4):41-46.(LI Qian，YANG Shu-geng.The finite element dynamic analysis for self-elevating platform by ANSYS/Multi-physics program［J］.China Offshore Platform，2003，18(4):41-46.(in Chinese))

［7］李明，陶正梁，姚海田.基于ANSYS的平台波流载荷下动力分析及疲劳分析［J］.石油钻探技术，2005，33(3):45-48.(LI Ming，TAO Zheng-liang，YAO Hai-tian.The dynamic and fatigue analysis for offshore platform under the wave and current forces by ANSYS［J］.Petroleum Drilling Techniques，2005，33(3):45-48.(in Chinese))

［8］刘翔，李刚，岳前进，等.抗冰导管架平台疲劳可靠性优化［J］.工程力学，2010，27(1):215-220.(LIU Xiang，LI Gang，YUE Qian-jin，et al.Optimization of ice-resistant jacket platform design based on fatigue reliability［J］.Engineering Mechanics，2010，27(1):215-220.(in Chinese))

［9］舒铁.单立柱海洋平台安全性评价研究［D］.大连:大连理工大学，2005.(SHU Tie.Study on safety evaluation for singleleg jacket platform［D］.Dalian:Dalian University of Technology，2005.(in Chinese))

［10］杨秀娟，修宗祥，闫相祯，等.深水导管架海洋平台随机疲劳寿命可靠性分析［J］.机械强度，2011，33(2):264-269.(YANG Xiu-juan，XIU Zong-xiang，YAN Xiang-zhen，et al.Random fatigue life reliability analysis of deep water jacket platform［J］.Journal of Mechanical Strength，2011，33(2):264-269.(in Chinese))

［11］谢文会，谢彬.深水半潜式钻井平台简化疲劳分析［J］.海洋工程，2010，28(2):37-43.(XIE Wen-hui，XIE Bin.Simplified fatigue assessment for deepwater semi-submersible rig［J］.Ocean Engineering，2010，28(2):37-43.(in Chinese))

［12］刘翔，李刚，岳前进，等.抗冰导管架平台疲劳可靠性优化［J］.工程力学，2010(10):215-220.(LIU Xiang，LI Gang，YUE Qian-jin，et al.Optimization of ice-resistant jacket platform design based on fatigue reliability［J］.Engineering Mechanics，2010(10):215-220.(in Chinese))