模糊递归神经网络在软测量中的应用

彭晓波

（湖南工业大学 电气与信息工程学院，株洲 412007）

0 引言

在现代工业过程中，对控制的要求越来越高。因而要达到较高的控制精度，必须对测量的各种过程变量也有很高的要求，一般解决工业过程测量精度不断提高的方法是研制新型的过程检测仪表，以满足生产过程中对质量和产量进行控制的要求。但是这类过程变量大都具有难测的特点，而且研制新型检测仪表成本非常高、研制周期长，测量对象、范围和功能都受到一定的限制；因此，有必要寻求一种新的思路。近年来在过程控制和检测领域涌现出的软测量技术正是这一思想的集中体现。

软测量建立待测变量与可测或易测过程变量之间的非线性函数关系，间接得到待测变量的估计值。经过多年的发展，已经形成了一些较为成熟的软测量建模方法：机理建模[1]；基于人工神经网络建模[2]；模糊建模[3]；集成建模[4]。机理模型是通过对机理过程中物质和能量的转化过程进行分析,得到机理数学表达式，每个系数均具有实际物理意义。但实际模型的结构是非常复杂，由于对生产过程的认识是不全面的，就导致了其检测精度就会随着生产过程的不同阶段，不同条件的变化而变化，从而无法建立较好的机理模型。神经网络是目前软测量研究中最活跃的领域，它是根据对象的输入输出数据直接建模，在解决高度非线性和严重不确定性系统控制方面具有巨大的潜力，特别适用于工业过程的软测量建模。但是，一般神经网络是一种静态映射，不适合用来表示动态映射[5,6]。而一般的生产过程都是动态的，因此动态递归神经网络对于动态过程的软测量，提供了一种极具潜力的选择，代表了神经网络软测量的发展方向。模糊理论模拟人类思维，是处理模型未知或具不确定性的复杂系统的一种有效手段。近年来，模糊理论与神经网络结合构成模糊神经网络大量应用于软测量中，它既有模糊逻辑表达定性知识的能力，又有神经网络很强的自学习和处理定量数据的能力，因而非常适合处理一些复杂的非线性软测量建模问题。

本文结合递归神经网络和T-S模糊模型，提出了基于T-S动态递归型模糊神经网络的软测量模型，不仅可以很好地反映动态的生产过程，还具有定性知识表达的能力，把它应用在冶炼过程，获得了很好的效果。

1 T-S动态递归型模糊神经网络(DTRFNN) 的结构

如图1所示，本文提出了DTRFNN结构。

DTRFNN被分为6层，形式如下：

Rule r：IFχ1(t) is Ar1andχ2(t) is Ar2and hr(t) is G Then y (t+1) =αr0+αr1+χ1(t) + …αrN+1h1(t)and… h1(t+1) isr1and… hr(t+1) isrr

这里描述DTRFNN：

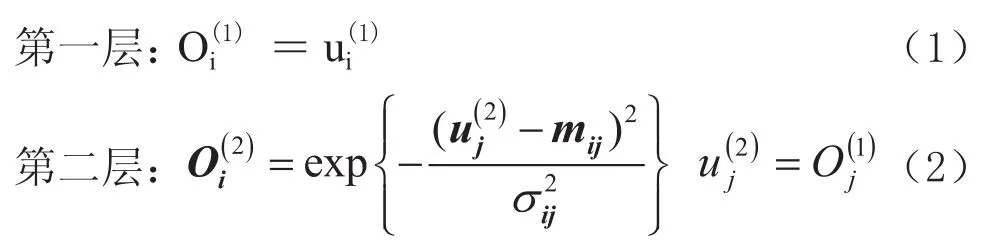
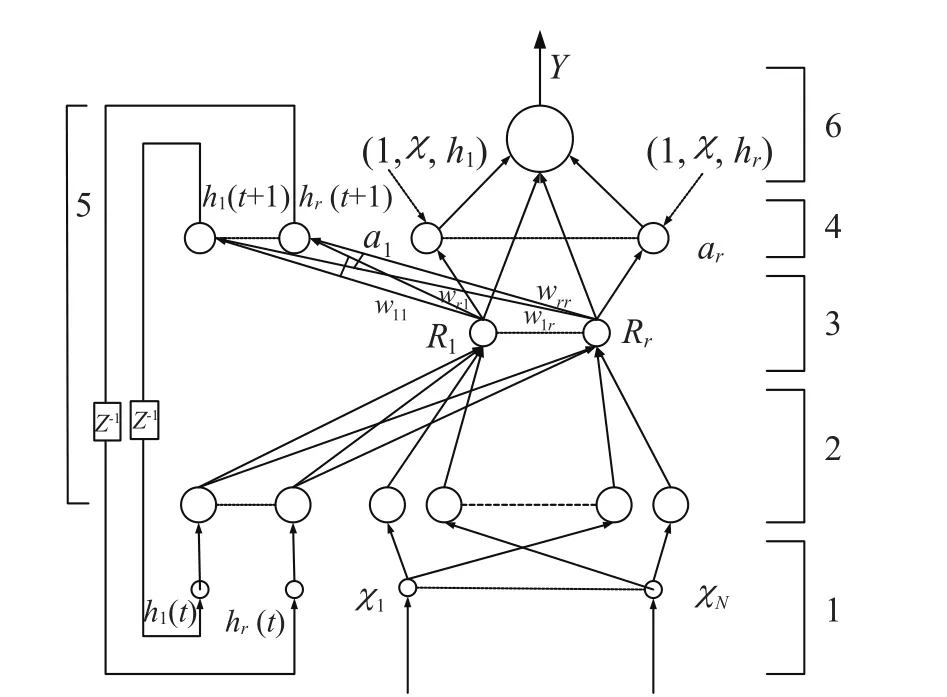
图1 DTRFNN 的结构

2 T-S动态递归模糊神经网络在工业过程软测量中的应用

冶炼过程和化工过程是非常复杂的动态工业过程，在反应过程中伴有强烈的氧化和还原反应、物相的变化及能量的转换。从控制的角度看,冶炼过程属于典型的非线性过程，是大滞后、强耦合、分布式的连续动态过程。现在的冶炼厂和化工厂控制系统一般采用DCS系统，采用前馈-反馈方式进行在线控制。在反馈控制中，某些金属的含量，金属化合物的温度、微量金属比等等工艺参数是重要的反馈信息，这些参数的稳定对生产的稳定至关重要。但是目前这些参数很多都是通过人工获得，测量值在时间和准确性上都严重影响了控制系统的效果，如果采用测量传感器，因为工艺原因，经常要更换，成本非常高，这样急需一套实用的软测量方法来满足生产的需要。因此，目前的参数测量方式很难保证生产过程长期稳定，导致了产量和质量很难有本质上提高，而且单位产量的能耗一直居高不下。针对工艺参数测量这个关键问题。本文采用了T-S递归模糊神经网络软测量模型，以解决以上的测量问题。

在某冶炼过程中，渣中金属的流失不可避免，但是如果有合适的铁硅比，可以大大的减少金属的流失，并且金属溶剂和渣的分层也是由铁硅比决定的，因此对铁硅比的测量直接影响到了金属的产量，但是铁硅比的测量都是由通过人工现场取样，然后再到化验室进行化验，这样会导致这些参数比实际参数要滞后很多，而且认为主观的因素占了很大一部分，因此测量值在时间上和准确性上都严重影响了控制系统的效果，本文采用T-S动态递归模糊神经网络对铁硅比进行软测量

对于这个软测量模型, 输入变量的选择是非常重要的。通常可以检测的间接变量有几十个，将这些检测变量都作为输入变量显然是不符合要求，而且也容易造成计算量的过大。因此输入变量的选择可根据工艺与实际经验来确定[7]，也可采用相关分析法[8]， 确定与被软测量变量最相关的几个间接输入变量。表一 给出了某冶炼过程中软测量模型的输入输出变量。

质量指标铁硅比作为控制目标量，即DTRFNN输出参数；氧、风、溶剂、精矿、烟灰、精矿成分11个量为操作参数，即DTRFNN的11个输入参数。

首先，根据现场采集到的大量数据(包括输入变量和输出变量) 对DTRFNN 进行学习。需要指出的是，在对输入、输出数据要进行预处理，因为数据随时可能出现“异常点”，还有数据归一化的问题，最重要是要考虑输出变量与输入变量的滞后问题。即t 时刻的数据(可以是化验分析值) 是与（T-S）时刻的输入数据对应的，根据工艺操作经验，S一般为60min。经过大量的数据仿真分析，最后确定DTRFNN 的结构为11-55-5-5-1，即输入变量为6个 ，第二层的节点数是55个，第三层和第四层的节点数都是5，输出变量为1个,即铁硅比。

对铁硅比给出了仿真结果，对几个月的生产数据进行处理、进行训练，50多组数据进行验证。在图2中，DTRFNN的结果用星号来表示，实际值用圆圈来表示。从数据中，我们可以知道DTRFNN平均准确率达到了很高。显示了DTRFNN能很好的对冶炼参数进行软测量。进行推广，DTRFNN也可以对复杂的大型工业过程参数进行软测量，为解决过程工业参数测量的难题提出了一条新的思路。

表1 参数软测量输入与输出变量

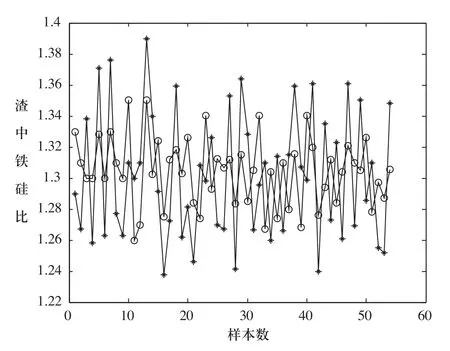
图2 渣中铁硅比的DTRFNN输出与实际值

3 结论

针对参数测量在过程工业中的问题，本文采用了DTRFNN动态软测量模型，对它的结构进行了描述。并结合在冶炼过程中金属元素含量的测量，结果表明，DTRFNN动态模型能很好的实现软测量，取得了良好的效果。

[1] 杨慧中.聚丙烯腈质量指标软测量模型的数据动态校核[J].华东理工大学学报, 2001, 27(5):536-639.

[2] 李勇刚,桂卫华,陈峰.基于因素分析的复合神经网络及其在软测量中的应用[J].信息与控制,2004,33(2):141-144.

[3] 马铭, 孟庆锴, 张利彪.基于模糊系统优化的软测量建模[J].辽宁工程技术大学学报, 2010, 29(5):763-766.

[4] 陈晓方, 桂卫华, 王雅琳, 吴敏, 阳春华.基于智能集成策略的烧结块残硫软测量模型[J].控制理论与应用, 2004,21(1): 75-80.

[5] C H Lin, W D Chou, F J Lin.Adaptive recurrent neural control for nonlinear syetem tracking.IEEE Proc.Control Theory Appl, 2001,148(2): 156-168.

[6] Tommy W S, Chow, Yong Fang.A recurrent neuralnetwork-based real-time learing control strategy applying to nonlinear systems with unknown dynamics.IEEE Trans.Indust.eLEC, 1998, 45(1):153-161.

[7] 于静江, 周春晖.过程控制中的软测量技术[J].控制理论与应用, 1996, 13 (2): 137-144.

[8] 宋德臻.软测量技术及其在工业过程中的应用[D].杭州:浙江大学, 1998.