地方政府收购中的融资优化应用研究——以小煤矿群整改为例

文 竹，文宗川，侯 剑

(1.内蒙古工业大学 管理学院，内蒙古 呼和浩特 010051;2.内蒙古工业大学 理学院，内蒙古 呼和浩特 010051)

引言

产业市场集中度的提高有利于煤炭产业利润和安全绩效的改善，中国煤炭产业的HHI值＜500，应该进一步提高市场集中度，通过兼并、重组等方法组建大公司、大企业(李艳梅，2007)。在资源浪费严重、生态环境恶化、矿难频发以及税费流失严重等背景下，以山西为代表的煤矿大省，掀起了一轮煤矿整改的热潮。其整改的预期效果是通过以中央煤炭企业为主的大型煤企兼并、重组中小煤矿，减少煤矿的总数量，提高产业的集中度，并保证政府的控股地位(绝对控股或者相对控股)。各煤矿大省的煤改前景是好的，但是过程却很艰辛。在煤矿整改中最棘手的问题就是地方政府以及收购企业资金不足，不能及时、足额地补偿被兼并煤矿矿主，从而造成煤矿主怨声载道，迟迟不肯退出历史舞台，形成煤矿整改过程中极大的阻力。

2008年下半年国家实施了积极的财政政策以后，各地地方政府一改往日融资渠道单一的状况，纷纷创新投融资模式，通过搭建政府融资平台，采取股权转让、发债、银行贷款等多种方式筹集资金(计承江，2010)。政府融资渠道的拓宽有利于解决煤矿整改中资金短缺的问题，但融资规模扩大带来的金融风险不容小视。在过去一年中，地方政府融资平台的数量和融资规模急剧膨胀，目前官方统计数量已经超过3千个，总体融资规模达到4到5万亿元，中国银监会已把地方融资平台风险列为2010年银行业3大风险之首(杨海霞，2010)。这就使得地方政府在融资初期做好还款计划显得十分重要。

按照现代企业优序融资理论，在市场经济下，企业优序融资的模式是先内源融资，再债务融资(包括发行债券和银行贷款)，最后才是股权融资。赵晓丽(2008)基于权衡理论、优序理论和技术评价理论，以综合融资成本最小化为目标，建立了水电企业债务融资与股权融资最优比例的模型，虽然模型针对的是水电企业，但其融资方式与本文中地方政府可采用的融资方式一样，本文参考了其建立模型时变量的设计方法。与企业融资不同，本文从中国实际情况出发，分析了地方政府在弥补整改煤矿的资金缺口时，利用上述各种方式融资的利弊，以财政支出最小化和政府控股权最大化为优化目标。考虑到当前地方政府债务风险较大的现实情况，将重点放在保证政府融资后每年的还款能够顺利进行上。利用优化理论，建立了模型，并分析了地方政府股权投资预期收益率变动对最优决策的影响。

一、煤矿整改中的地方政府融资方法

(一)矿权转股权

若干煤矿整改合并，可以适当地让民营资本入股。在收购私人矿权时，可以利用矿权转股权的方法，将一部分矿主的矿权折算成股份，这种方法的优点就是不需要政府出资，缺点是造成企业股权分散，同时政府将失去相应股份的分红。

(二)银行贷款

按照《商业银行法》和《贷款通则》，商业银行不得向政府机构发放贷款，但通过设立各类投融资机构借款，地方政府实际向商业银行进行了大量的融资(李俊文，2008)。银行贷款的优点是可以一次性大规模的资金融入，缺点是银行资金大多来源于存款，有较高的成本(包括利息成本和经营成本)，所以银行贷款利率较高。同时银行为了降低自己的风险，多采用等额本息的还款方式，这样会增大政府每期的还款压力。

(三)发行地方债

从2009年开始，国家允许各省、市、自治区政府发行地方债。就目前来看，地方债发行规模一般都在三十亿左右，最高的不超过百亿元，发行利率集中在1．6% －2．36%之间，期限都是3年(数据来源:上海证券交易所)。地方债每年按票面利率支付固定的利息，到期一次性归还本金加最后一期利息。其优点是将融资对象从单纯的银行扩大到非银行金融机构及民众，资金来源更广泛，利率低于银行贷款利率。缺点是期限短，短期还款压力大。

二、政府融资的优化模型

政府整改的目标是将众多分散的私有煤矿整合成几个大型的国有控股煤矿。整改方式有两种，一是成立新的国有控股公司，二是利用现有大型煤炭中央企业进行并购。两种方式都面临着资金短缺问题，都需要通过融资来解决，不同的是融资后最终还款人一个为政府，一个为中央企业。本文以第一种整改方式为例进行建模。

模型建立的假设条件如下:

(1)若干私有煤矿整改后形成一个新的大型煤炭企业;

(2)政府对该煤炭企业实现控股;

(3)整改形成的新公司，从见效益开始，每年预期分红率固定;

(4)政府每年财政收入(不包括新公司分红)中用来偿还整改借款的资金额度相等。

假设期初需整改的若干私营煤矿的总价值为W，上述三种融资手段的融资规模的比例分别为y1，y2，y3，政府期初出资比例为 y4，于是有:

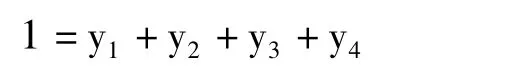
为了保证政府的控股地位，需有1－y1≥M0。

其中M0为保证政府控股(绝对控股或相对控股)的最低持股比例。若政府计划为第n年末还清所有债务，新公司从第k1年底开始分红，预期分红率为r1;银行贷款年利率为r2，第n年末还清;地方债票面年利率为r3，第k3年到期;政府计划每年财政收入(不包含新公司红利)中用于偿还债务的资金额度占W的比例为y5，市场利率为r。考虑到政府实际财政压力，模型中添加约束条件:

y4≤M1(政府期初能出的最大资金额同W的比例)

y5≤M2(政府后续还款中每年能出的最大资金额同W的比例)

模型优化目标为:

目标1(控股权最大化)为:minz1=y1

目标2(期初财政支出最小化)为:minz2=y4

目标3(后续财政支出最小化)为:minz3=y5

于是可以建立优化模型:

minz1=y1

minz2=y4

minz3=y5

约束条件:

y4≤M1

y5≤M2

y1+y2+y3+y4=1

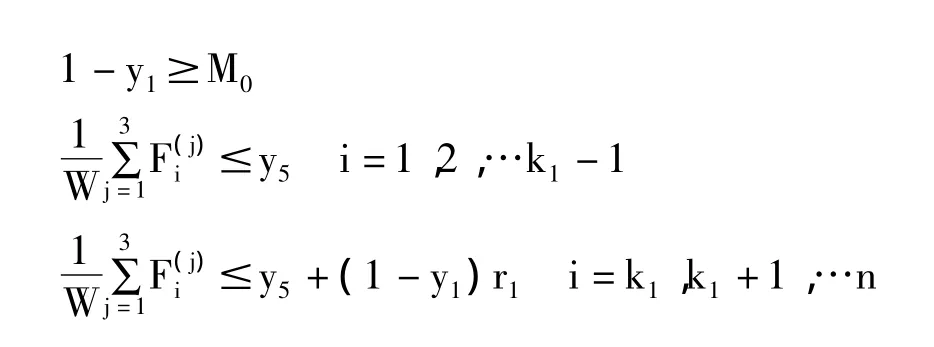
yj≥0 j=1，2，3，4

一般银行采取等额本息的还款方式，所以第(2)种融资手段在第i年造成的政府资金流出

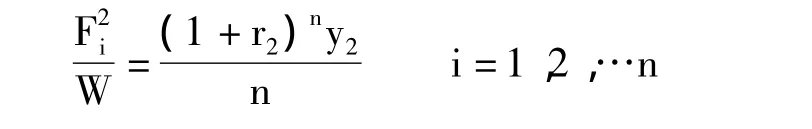
地方债前几年只支付利息，到期归还本金加最后一期利息，所以第(3)种融资手段在第i年造成的政府资金流出

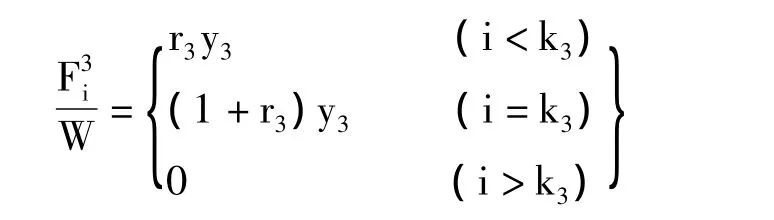
上述模型是一个多目标的线性规划问题，可以转化为一个目标规划来求解。转化后模型的优化目标变为:

其中w1，w2，w3为权系数。权系数的变化对模型最优解有重要的影响(赵可培，2008)，本文通过现值的比较来确定权系数:

新公司投产后后续每年分红的现值为:

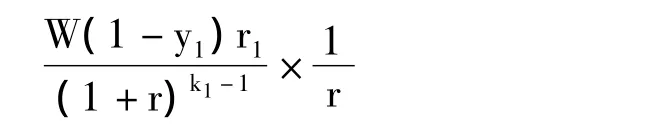
政府期初出资为Wy4

政府每年利用财政收入(不包括新公司分红)固定还款的现值为:y1每减少一个单位，相当于y4增加个单位。

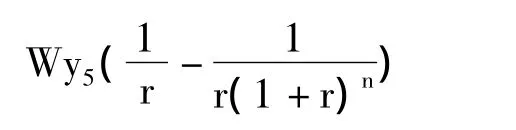
y5每增加一个单位，相当于 y4增加

三、利用模型进行实证分析

(一)数据来源与描述

我们取最近发行的十个地方债利率的平均值2．198作为模型中的地方债利率，期限为3年，取最近一次利率调整日期2008年12月23日的中央银行一年期贷款基准利率5．31%作为模型中的银行贷款年利率，市场利率同比一年期银行存款利率2．25%(数据来源:中国人民银行)。一般公司的培养期为3年，所以可假设新公司第3年底开始分红。本文作了一个5年的规划，即政府所有借款在第5年底还清。政府实现绝对控股(即y1＜50%)，同时限制M1=M2=15%。

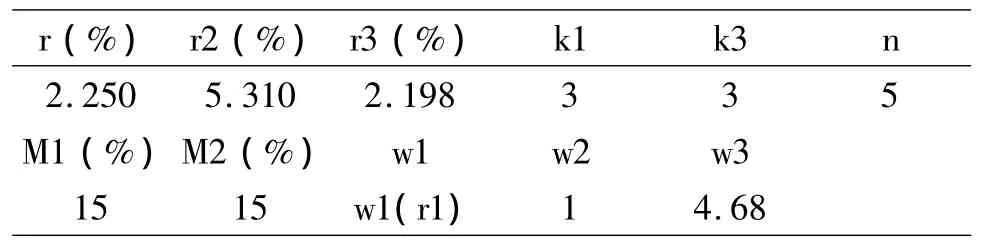
表1 各参数列表

(二)规划求解结果

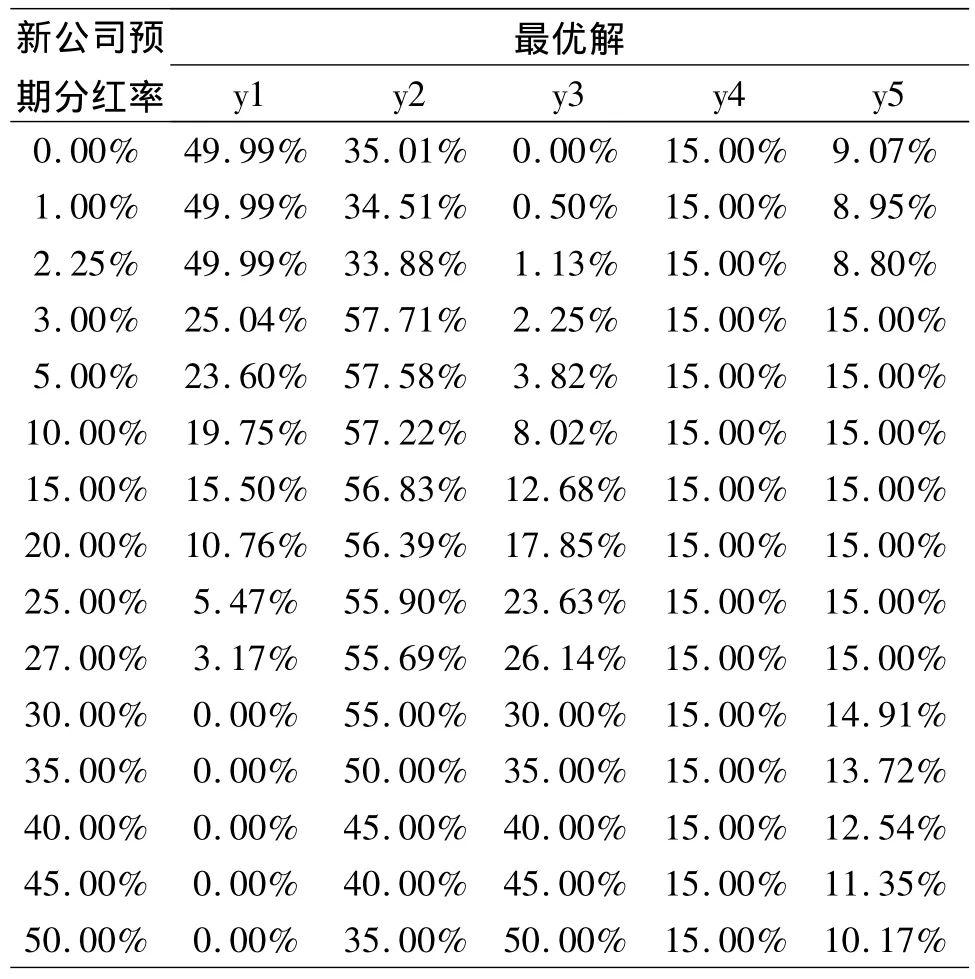
表2 新公司预期分红率对模型最优解的影响

通过规划求解，我们可以得到新公司不同预期分红率下上述模型的最优解状况。

(三)实证分析结果解释

当新公司的预期分红率比较低时，政府的最优选择应该是在保证国有控股的前提下尽可能的利用矿权换股权手段来缓减收购资金的压力，随着新公司预期分红率逐渐提高，最优策略中矿权换股权和银行贷款的比例要逐渐下降，利用地方债融资的比例逐渐提高。无论新公司预期分红率怎么样，政府期初出资比例都要维持在能承担的最大限度上。在本例的参数下，当新公司的预期分红率超过30%时，则选择最优策略时，应该完全放弃矿权转股权的行为。

四、结论及展望

在整改煤矿过程中，解决资金问题的渠道有多种。在保证政府的还款计划能够顺利实施，同时国有控股的目的能够实现的条件下，各种渠道如何搭配有一个最优化的选择。在实际整改过程中，根据实际情况确定了模型中的各种参数后，则可以利用本文中建立的优化模型，得出一个最佳搭配比例。

如果地方债通过“荷兰式”的招标方式发行，则发行利率由竞拍形成，会受到发行规模的影响，即r3=r3(Wy3)，在这种情况下上述模型就转化成了一个非线性模型，求解将会变得困难。解决的方法是如果条件允许，可以将地方债的发行安排在其他融资方式的最前面，等发行结束，确定了地方债的融资规模W和息票率后，再代入上述模型，对其他四个变量进行求解。

本文建立的模型提供的融资方案也可以应用到任何行业的以国有控股为目标的整改中。

［1］ 李艳梅．中国煤炭产业集中度与绩效的实证分析［J］．北京交通大学学报，2007，(3):11－14．

［2］ 彭晓英．基于EDA模型的煤炭上市公司股权融资效率评价［J］．中国矿业，2008，(12):25 －29．

［3］ 计承江．关于政府融资平台发展问题的探讨［J］．金融理论与实践，2010，(1):4 －6.

［4］ 刘降斌．我国政府投资项目融资机构优化分析［J］．经济研究导刊，2006，(5):101 －103.

［5］ 杨海霞．地方政府融资风险难题——规范地方融资［J］．中国投资，2010，(3):37 －41.

［6］ 赵晓丽．水电企业融资组合优化模型设计［J］．技术经济，2008，(5):68 －73.

［7］ 赵可培．运筹学［M］．上海:上海财经大学出版社，2008．

［8］ 张亦春．金融市场学［M］．北京:高等教育出版社，2008.

［9］ 郑荣鸣．中外企业融资结构比较分析［J］．会计研究，2004，(7):67 －71.

［10］ 雷辉．上市公司并购融资方式与治理绩效研究［J］．财经理论与实践，2009，(11):42 －45.

［11］ 李俊文．地方政府机构的银行融资情况研究［J］．经济问题探索，2008，(10):110 －117.

［12］ 秦成逊．西部地区地方债融资探析［J］．经济问题研究，2009，(12):37 －42.

［13］ 石绍宾．地方债为公共品融资:条件与效应分析［J］．税务与经济，2007，(2):24－28.

［14］ 刘红霞．中小企业融资方式机构优化问题研究［J］．生产力研究，2007，(24):108 －110．

［15］ 王顺金．融资方式规划的Excel模型设计［J］．中国管理信息化，2006，(6):34 －38.

［16］ JoséIgnacio Munoa．Optimal Investment portfolio in renewable energy:The Spanish case［J］．Energy Policy，2009，(37):5273 －5284.

［17］ Catherine Casamatta．Optimal Financial Contracts with Venture Capitalists［J］．The Journal of Finance ，2003，(10):2059－2085.

［18］ WB Elliott．Market timing and the debt－ equity choice［J］．Journal of Financial Intermediation，2008，17(2):175－197.

［19］ JB Guerard．Debt，Equity，The Optimal Financial Structure And The Cost Of Funds［M］．Springer US，2007.

［20］ Robert A．Jarrow．On Model Testing in Financial Economics［J］．Financial Review，2010，45(2):277 －285.