装有平衡悬架半挂汽车列车的平顺性建模与仿真分析

李相彬，赵又群

(南京航空航天大学能源与动力学院，南京 210016)

半挂汽车列车是由半挂牵引车与一辆半挂车组合而成的汽车列车，它主要用于中长途货物的运输。由于半挂汽车列车的装载能力大，因此在使用过程中其载货质量变化比较大，而悬架的刚度也大，故不平路面的激励更容易传到车身及驾驶室。根据各项统计分析和试验结果，在各类公路行驶车辆中，半挂汽车列车的平顺性最差。因此，多年来半挂汽车列车的平顺性一直是国内外学者的研究重点［1－2］。

本文以装有平衡悬架并采用全浮式驾驶室的半挂汽车列车为研究对象，根据其实际结构，采用1/2车模型，建立半挂汽车列车的11自由度振动系统模型。用路面不平度功率谱密度构造路面输入的功率谱矩阵，利用随机响应计算方法中频域法的频率响应函数，对汽车进行随机振动分析，并计算驾驶室质心位置的垂直方向加速度均方根值，为该型车平顺性的设计和改进提供建议。

1 半挂汽车列车平顺性模型

平顺性主要研究汽车在不平路面等外界激励下所产生的振动和冲击导致人感到不舒适、疲劳甚至损坏健康的性能。根据路面不平的统计特性和人体对振动的响应特性，平顺性研究的频率范围在50 Hz之内，尤其在20 Hz之内。为了简化分析模型，建立了多自由度的半挂汽车列车1/2车振动模型，如图1所示。

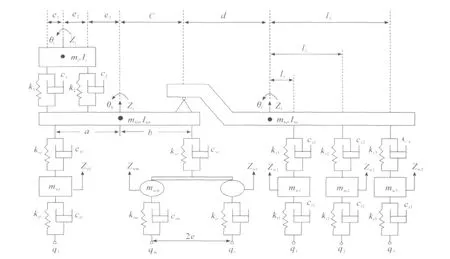
图1 车辆11自由度振动模型

模型分析假设:

1)汽车沿纵向中心线左右对称，并作匀速直线运动;

2)车身在平衡位置附近作微幅振动，车身质心在轴向面内的振动忽略不计，车体绕Z轴的角振动忽略不计;

3)平衡悬架的钢板弹簧可视为弹性弹簧与刚性平衡杆2个分开的元件，忽略平衡杆的转动惯量，平衡杆的质量等分给牵引车中、后车轴;

4)刚性平衡杆和中、后车轴以铰接的形式连接;

5)牵引车与半挂车之间以铰接的形式连接;

6)忽略除路面以外的其他振源［3］。

该模型考虑11个自由度:驾驶室的垂直运动Zj、俯仰运动θj;牵引车车身的垂直运动 Zb、俯仰运动θb;半挂车的俯仰运动θt;牵引车各个轴的垂直运动 Zwf、Zwm、Zwr;半挂车各个轴的垂直运动Zw1、Zw2、Zw3。

需要注意的是，由于受鞍座的约束，半挂车的垂直运动和俯仰运动只有1个有效自由度。半挂车的垂直运动位移Zt、俯仰运动角θt和牵引车的垂直运动位移Zb、俯仰运动角θb有如下数学关系

图1 中各符号意义:mi、mhb、mht分别为驾驶室、牵引车车身、半挂车车身质量;Ii、Ihb、Iht分别为驾驶室、牵引车车身、半挂车车身面内转动惯量;mwf、mwm、mwr分别为牵引车前轴、中轴、后轴非簧载质量;mw1、mw2、mw3分别为半挂车1 轴、2 轴、3 轴非簧载质量;a，b分别为牵引车车身质心至前轴、中后轴中心的纵向距离;c、d分别为牵引车质心、半挂车质心至鞍座的纵向距离;2e为牵引车中后轴纵向距离;e1、e2分别为驾驶室质心至驾驶室前、后悬置纵向距离;e3为牵引车质心至驾驶室后悬置纵向距离;l1、l2、l3分别为半挂车车身质心至1轴、2轴、3轴中心的纵向距离;k1、k2分别为驾驶室悬置的前后弹簧刚度;c1、c2分别驾驶室悬置的前后减震器阻尼;ksf为牵引车前轴悬架垂直刚度;csf为牵引车前轴悬架垂直阻尼;ksr为牵引车中后轴平衡悬架垂直刚度［4］;csr为牵引车中后轴平衡悬架垂直阻尼;ktf、ktm、ktr分别为牵引车前轴、中轴、后轴的轮胎刚度;ctf、ctm、ctr为分别为牵引车前轴、中轴、后轴的轮胎阻尼;ks1、ks2、ks3分别为半挂车1轴、2 轴、3 轴悬架垂直刚度;cs1、cs2、cs3分别为半挂车1 轴、2 轴、3 轴悬架垂直阻尼;kt1、kt2、kt3分别为半挂车1轴、2轴、3轴的轮胎刚度;ct1、ct2、ct3分别为半挂车1轴、2轴、3轴的轮胎阻尼;qf、qm、qr、q1、q2、q3分别为牵引车及半挂车各轴路面对轮胎激励;Zwf、Zwm、Zwr分别为牵引车前轴、中轴、后轴非簧载质量的垂向位移，图示方向为正;Zw1、Zw2、Zw3分别为半挂车1轴、2轴、3轴非簧载质量的垂向位移，图示方向为正;Zj、Zb、Zt分别为驾驶室质心、牵引车车身质心、半挂车车身处的垂向位移，图示方向为正;θj、θb、θt分别为驾驶室、牵引车车身、半挂车车身面内转动角度，图示方向为正。

用拉格朗日法［5］建立矩阵形式的微分方程为

式(2)中:

位移向量

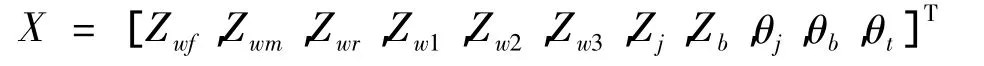
质量矩阵

其中 Mt=diag(mwf，mwm，mwr，mw1，mw2，mw3，mj)。

阻尼矩阵

其中

刚度矩阵K的形式和阻尼矩阵C的形式相同。

广义激励力矩阵

式(3)中:KT、CT分别为轮胎的广义刚度矩阵和广义阻尼矩阵分别为路面垂直位移输入和速度输入。

2 半挂汽车列车平顺性分析

为了求出车辆在不同等级路面的响应，采用频域分析的方法对模型进行求解。在线性系统中，根据随机振动理论，有

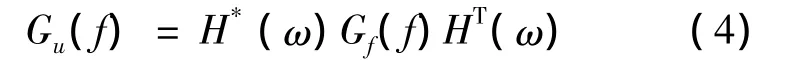
式(4)中:Gu(f)为振动响应的功率谱密度;Gf(f)为路面输入的功率谱密度;H*(ω)为系统频率响应函数矩阵的共轭;HT(ω)为系统频率响应函数矩阵的转置，并且ω=2πf。

对式(2)进行傅里叶变换，可求出系统的频率响应函数为

根据GB 7031《车辆振动输入——路面不平度表示》中的建议，空间频率路面谱密度的拟合表达式为

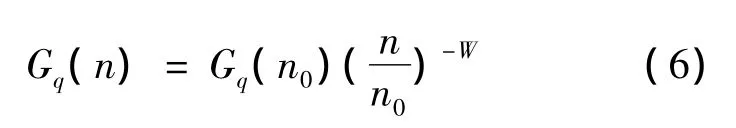
换算为时间频率功率谱密度

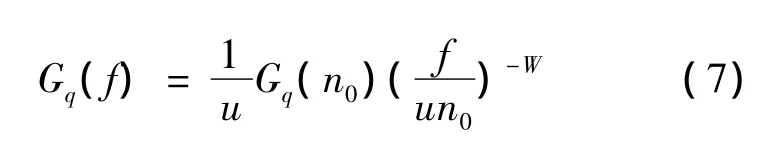
式(6)、(7)中:Gq(n0)为路面不平度系数(m3);n为空间频率(m－1);n0为参考空间频率，取n0=0.1 m－1;W为频率指数，取 W=2;u为车速(m/s);f为频率(Hz)。

路面输入的功率谱密度矩阵［6］

式(8)中:L1=a+b－e;L2=a+b+e;L3=a+c+d+l1;L4=a+c+d+l2;L5=a+c+d+l3。

将式(5)和式(8)带入式(4)，便可得到系统对不同等级路面输入的频率响应。

对于平顺性的评价，需要计算由路面激励传递至人体的振动响应。求得位移响应的功率谱密度后，根据式(9)可求得加速度响应功率谱密度

再根据式(10)计算出频率加权后的加速度均方根值

本文只考虑垂向运动，因此频率加权函数W(f)可用式(11)表示

加权加速度均方根值是汽车平顺性的最终评价指标，反映了驾驶员舒适性的好坏。

3 计算实例

根据上述理论，采用Matlab编制软件［7］。以某半挂汽车列车为例，选取不同等级路面和不同车速进行随机响应仿真分析［8］。

图2给出该车分别在A级路面(Gq(n0)=16×10－6m3)、B 级路面(Gq(n0)=64×10－6m3)、C级路面(Gq(n0)=256×10－6m3)，车速为 60 km/h条件下，驾驶室质心处的垂向加速度响应功率谱密度曲线。图3给出该车在B级路面，车速分别为30、60、80 km/h条件下，驾驶室质心处的垂向加速度响应功率谱密度曲线。由图2和图3可知:随着路面状况变差，驾驶室质心处的振动增大;车速的提高会降低车辆的平顺性能。

图2 车速60 km/h驾驶室质心位置垂直加速度功率谱密度

图3 B级路面驾驶室质心位置垂直加速度功率谱密度

此外，还计算了上述5种不同行驶条件下驾驶室质心处的垂向振动加权加速度均方根值，结果列于表1中。从表1中也可以看出，差的路面状况和高车速都会降低车辆的平顺性。

表1 不同行驶条件下驾驶室质心处加速度均方根值

4 结束语

以装有平衡悬架并采用全浮式驾驶室的半挂牵引车为研究对象，建立了11自由度的结构系统振动模型，适用于半挂牵引车振动系统响应的预测和分析，能反映系统振动性能的好坏，迅速求出半挂汽车列车的振动响应的主要数值，为参数的选择匹配提供方便，提高了半挂汽车列车的设计效率。

［1］余志生.汽车理论［M］.4版.北京:机械工业出版社，2006.

［2］范 永法.牵引车－半挂车乘坐舒适性的优化与分析［J］.汽车工程，1989(1):53 －65.

［3］秦 玉英.汽车行驶平顺性建模与仿真的新方法研究及应用［D］.长春:吉林大学，2009.

［4］蒯 行成，李用红，任恒山.采用平衡悬挂系统的载重汽车的随机响应分析［J］.湖南大学学报，2005，32(2):25－28.

［5］胡海岩.机械振动与冲击［M］.修订版.北京:航空工业出版社，2002.

［6］何 仁，李丽.重型牵引车平顺性的预测与分析［J］.机械设计，2008，25(3):56 －59.

［7］王 诚，宋东璠.冯晓强，等.基于matlab和zemax模拟双透镜耦合系统［J］.激光杂志，2010，31(2):17－19.

［8］薛 定宇，陈阳泉.高等应用数学问题的MATLAB求解［M］.2版.北京:清华大学出版社，2008.

［9］何 仁，孙丽.轻型客车平顺性优化设计与试验评价［J］.重庆理工大学学报:自然科学版，2010(10):13－17.

［10］过吉生，欧健，陈毅挺，等.基于虚拟样机技术的CNG轿车平顺性仿真分析［J］.重庆工学院学报:自然科学版，2009(8):10－14.