粒子群算法在等效系统拟配中的应用

林 敏， 徐浩军， 薛 源， 苏 晨

(空军工程大学工程学院，西安 710038)

0 引言

对于现代战斗机，由于在气动布局、结构、动力系统等先进技术的应用及飞行控制系统的日益完善，组合系统的特征方程的阶次越来越高。在对飞机的飞行品质进行评定时，通常采用的方法是等效系统法，飞行品质规范MIL－F－8785C和MIL－HDBK－1797A中都对等效系统准则作了相应的规定。等效系统法是将飞机的操纵系统和飞机本体组成的高阶系统等效拟配成体现典型模态特性的低阶系统，从而依据飞行品质规范进行等级评定［1］。

对等效拟配问题的研究已取得一些相关成果。文献［1］针对遗传算法在全局搜索性能与收敛速度间的矛盾，将改进遗传算法应用于等效系统拟配;文献［2］采用最小二乘法与频域极大似然法求解飞机的低阶等效系统，依据参数辨识结果进行评价;文献［3］采用阻尼最小二乘法拟配飞机的长、短周期反应，表明其效果较好;文献［4］介绍了模式搜索算法进行参数优化，并取得较好的仿真结果。然而，最小二乘法等优化算法对初值依赖性较强，若选取不当，可能出现不合理的解;遗传算法则操作复杂，解高维问题时收敛速度慢，且容易陷入局部最优解。

粒子群优化算法［5］(Particle Swarm Optimization，PSO)是J.Kennedy博士和R.Eberhart博士提出的一种种群优化算法，源于对鸟群捕食的行为研究。系统初始化一组随机解，粒子通过迭代在解空间追随最优的粒子进行搜索，搜寻最优值。PSO算法基于种群算法的全局搜索策略，采用简单的速度－位置模型，保留特有的记忆性，具有个体数目多、计算简单、鲁棒性好等优点，适合于多维连续优化问题求解，已广泛应用于科学与工程等领域［6－7］。等效系统拟配是寻求等效系统数学模型中各个参数的值，使得高低阶系统频率特性最接近的过程，在数学上，这是一个参数最优化问题。PSO利用随机初始化的粒子，在参数要求的限定范围内，按照粒子速度－位置进化方程更新自己的速度位置，寻求等效模型参数的最优值。

本文分析了等效系统拟配的数学模型和目标函数;引进了自适应调节粒子速度经验权重的控制参数，并将改进的粒子群优化算法应用于实例中，采用失配度和失配包线对结果进行了检验，结果均满足品质规范的要求。

1 粒子群优化算法及改进

在PSO系统中，每个备选解被看作是在多维搜索空间中一个没有重量和体积的粒子i，多个粒子共存、合作寻优(近似鸟群寻找食物)，每个粒子根据它自身的“经验”和群体的最佳“经验”进行动态调整飞行速度，搜索最优解。

假设搜索空间是n维，粒子群由m个粒子组成。Xi=(xi1，xi2，…，xin)表示 n维空间中的第 i粒子的位置，xij∈［xjmin，xjmax］，j∈［1，n］;第 i个粒子的速度表示为 Vi=(vi1，vi2，…，vin)，vij∈［vjmin，vjmax］。粒子 i的速度 － 位置的进化方程为［8－9］

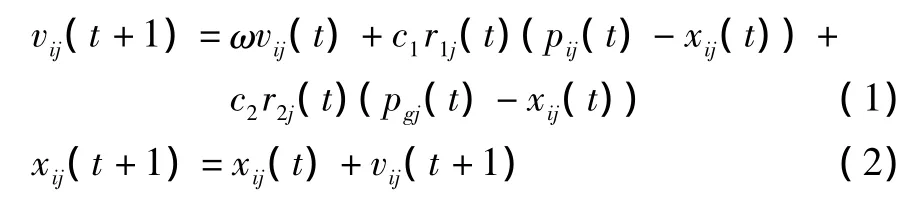
其中:i=1，2，…，m 为粒子的个数;j=1，2，…，n 表示粒子的维数;ω为惯性权重;c1，c2为加速度权重;r1，r2是介于［0，1］之间服从均匀分布的随机数;Pi=(pi1，pi2，…，pij)是粒子i当前所经历的最优位置，称为个体最优位置;Pg=(pg1，pg2，…，pgj)是整个群体中所有粒子所经历的最优位置，称为全局最优位置。

为平衡粒子群的全局探索和局部搜索能力，避免算法过早收敛而陷入局部最优点，提高解的精度。引进自适应调节参数φ1，φ2，其中，φ1为一函数值小于1的线性递减函数，使得群体在进化初期，尽量考虑粒子自身的因素，使得粒子在前期具有较高的全局搜索能力;φ2为一函数值小于1的线性递增函数，使得群体在进化后期尽量考虑群体共享信息，使得粒子具有较高的局部开发能力以加快算法的收敛速度。将式(1)改进为

其中:φ1=1为(0，1)之间的系数。

2 基于粒子群算法的等效系统拟配

2.1 低阶等效系统模型

在飞机横航向运动中，飞行员最关心的运动参数为飞机滚转角γ和侧滑角β，根据飞行品质规范MIL－F－8785C，可以得到横航向运动等效系统的数学模型为

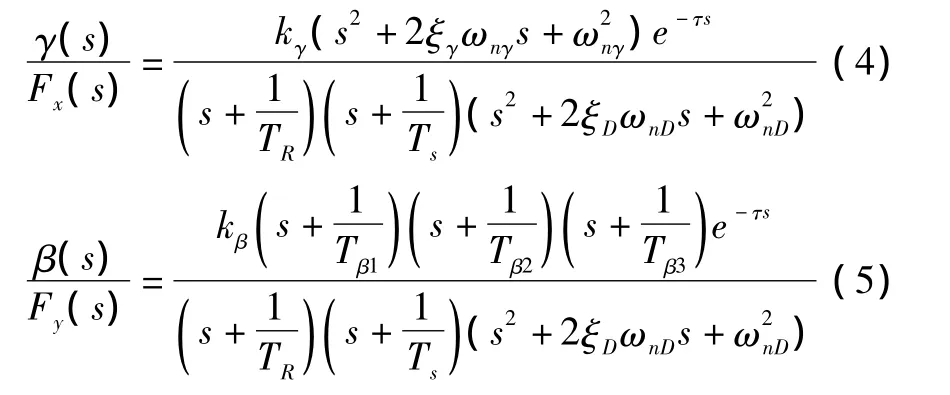
在频率域内进行等效系统拟配，将横向和航向分开考虑，目标函数(失配度)为

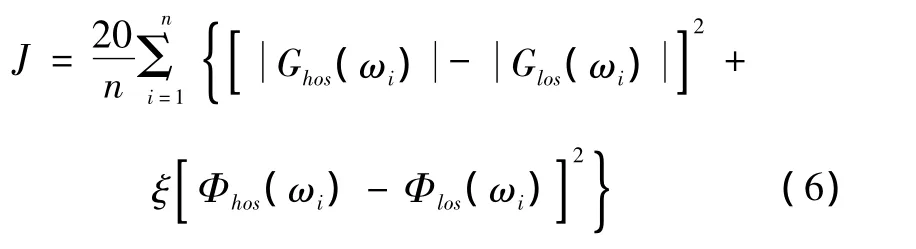
式中:n为所选取的频率点数，一般取20;ω为拟配频率点，在0.1～10 rad/s的范围内按对数坐标n等分选取;Ghos，Φhos分别为高阶系统频率特性的幅值和相位;Glos，Φlos分别为低阶系统频率特性的幅值和相位;ξ表示幅值偏差和相位偏差之间相对重要性的加权因子，一般取为 0.01745 dB/(°)。

2.2 拟配过程

1)初始化。设定种群规模N和迭代次数T。并用预定义的值域随机初始化粒子群中的粒子的位置和速度。

2)计算每个粒子的适应值J(Xi)，并以此初始化个体最优Pi，以种群中最好适应值的粒子初始化全局最优Pg。

3)根据式(2)、式(3)更新粒子的位置和速度。

4)当 vij＞ vjmax或 vij＜ vjmin，则令 vij=vjmax或 vij=vjmin;当 xij＞ xjmax或 xij＜ xjmin，则令 xij=xjmax或 xij=xjmin。

5)如果粒子的适应值J(Xi)优于Pi的适应值，则Pi更新为新位置;反之，Pi保持不变。

6)如果粒子的适应值J(Xi)优于Pg的适应值，则Pg更新为新位置;反之，Pg保持不变。

7)循环迭代，检查结束条件，若满足，则寻优结束，输出全局最优粒子Pg和最优适应值;若未达到最大收敛代数，则返回步骤3)，结束条件为寻优达到的最大进化代数tmax，或适应值小于给定精度。

3 仿真分析

以飞机横向运动参数滚转角单拟配计算过程为例进行仿真验证。其拟配模型如式(4)，共有8个待拟配参数 kγ，ξγ，ωnγ，τ，TR，Ts，ξD，ωnD。依据飞机飞行品质规范中的等级要求，设定各参数的拟配区间取为kγ∈［－50，50］，ξγ∈［0，2］，ωnγ∈［0，20］，τ∈［0，0.25］，TR∈［0，10］，Ts∈［0，500］，ξD∈［0，1］，ωnD∈［0，10］。依据仿真的精度要求，设置迭代次数为100次，粒子数目为50个。

选取5个状态点，在0.1～10 rad/s的范围内，按等间隔对数频率取20个点，按照拟配的要求进行了拟配计算，拟配计算结果见表1。

表1 系统等效拟配结果Table 1 Equivalent system analog-matching result

由表中数据可见，拟配目标函数(失配度)J的值均较小，满足品质规范所规定的失配度不大于20的要求。其中h=6 km，Ma=0.6时的高阶系统和等效低阶系统的幅值、相角曲线如图1、图2所示(图中，实线为高阶系统，虚线为低阶等效系统)。由图可见，高阶系统和低阶等效系统的幅值、相频曲线都拟配得很好。

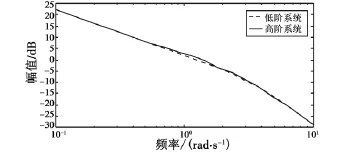
图1 幅值对比曲线Fig.1 Magnitude comparison curve

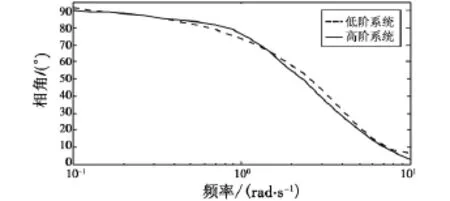
图2 相角对比曲线Fig.2 Phase comparison curve

在实际应用中，MIL－HDBK－1797A建议使用失配包络线作为拟配精度的检验［10］，在飞行员对飞机动态特性最为敏感的频率区域(1～4 rad/s)内，要求高低阶系统的幅相失配量处于失配包络线内。图3为高低阶系统的幅值失配包络图，图4为高低阶系统的相角失配包络图。从失配包络图中可以发现，在所选取的频率点上，失配量均处于失配包络线内，因此，拟配结果是可用的。

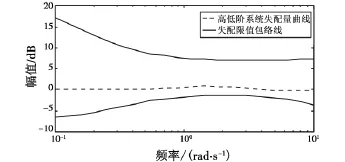
图3 幅值失配曲线Fig.3 Magnitude error curve

图4 相角失配曲线Fig.4 Phase error curve

由此，PSO算法在各拟配参数要求的范围内随机初始化粒子的初值，不需要确定各个拟配参数的初值，克服了初值选取不当的问题;根据改进的粒子速度－位置进化方程，易更新粒子的速度位置，并将优化解限定在该范围内，避免出现不合理解。仿真结果均满足符合品质规范的要求。

4 结论

仿真结果验证了PSO算法应用到等效系统拟配计算中的有效性和可行性。相对于遗传算法等群体智能算法，PSO算法结构简洁，易于实现;粒子从随机初始状态出发，克服了初值选取不当的问题，具有随机性和全面性;引进自适应调节参数，可以平衡算法的全局搜索和局部开发能力，避免过早陷入局部最优，这对解决多维寻优问题是非常重要的。尽管如此，算法还有许多不足之处，如粒子位置和速度更新中随机性的选择，如何在迭代后期进行算法的动态调节及保持粒子多样性，在提高运算速度的同时有效规避陷入局部最优，这些改进将有利于求得等效拟配的最优解。

［1］杨蔷薇，张翔伦.遗传算法在等效系统拟配中的应用［J］.飞行力学，2005，23(3):45-47.

［2］孟捷，徐浩军，葛志浩.等效系统参数辨识法在飞行品质评价中的应用［J］.数学的实践与认识学，2008，38(8):79-84.

［3］陈桂孙，方振平.俯仰轴飞行品质中等效系统准则的计算与模拟［J］.飞行力学，2003，21(1):16-20.

［4］田海燕.飞行品质中低阶等效系统的研究［D］.西安:西安电子科技大学，2008.

［5］纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京:科学出版社，2009.

［6］邹刚，孙即祥，敖永红.粒子群优化的聚类方法在图像分割中的应用［J］.电光与控制，2009，16(2):5-6.

［7］章魁，曲立国，黄友瑞.一种改进的PSO算法在PID参数优化中的应用［J］.电光与控制，2008，15(2):58-61.

［8］汪定伟，王俊伟，王洪峰，等.智能优化方法［M］.北京:高等教育出版社，2007.

［9］王德强.基于改进粒子群算法的PID控制器参数整定［D］.南京:南京信息工程大学，2008.

［10］Anon.Flying qualities of piloted aircraft，MIL-HDBK-1797［M］.USA:Department of Defense，1997.