一种初始种群算法的应用研究

姜彬峰

（吉林铁道职业技术学院 计算机科学技术系，吉林 132001）

0 引言

在日常生产实践中，我们往往会遇到一些约束优化问题。为了更好地使用计算机求解这些问题，人们普遍采用遗传算法。遗传算法（Genetic Algorithm,GA）是近几年发展起来的一种崭新的全局优化算法。它是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，1962年霍兰德(Holland)教授首次提出了GA算法的思想，1975年他发表《Adaptation in natural and artificial systems》的专著，如今发展成为标准形式的遗传算法。

遗传算法作为一种快捷、简便、容错性强的算法，在各类结构对象的优化过程中显示出明显的优势。与传统的搜索方法相比，遗传算法具有如下特点：

搜索过程不直接作用在变量上，而是在参数集进行了编码的个体。此编码操作， 使得遗传算法可直接对结构对象（集合、序列、矩阵、树、图、链和表）进行操作。搜索过程是从一组解迭代到另一组解，采用同时处理群体中多个个体的方法，降低了陷入局部最优解的可能性，并易于并行化。采用概率的变迁规则来指导搜索方向，而不采用确定性搜索规则。对搜索空间没有任何特殊要求（如连通性、凸性等），只利用适应性信息，不需要导数等其它辅助信息，适应范围很广。广泛应用在函数优化、组合优化、生产调度问题、自动控制、机器人学、图象处理、人工生命、遗传编码和机器学习等领域。

遗传算法的基本流程如图1所示。

l）产生初始群体，随机产生m个个体，每个个体看作是一个染色体，m个染色体组成一个群体；

2）对群体中每个个体计算相应的适应度值；

3）通过选择和复制操作从群体中选出满足条件的个体，并放入到交配缓冲池中；

4）对交配缓冲池中的个体使用交叉和变异算子形成下一代群体中的m个个体；

5）计算每个新个体的适应度值；

6）如果满足结束条件，则停止；否则转到第3步。

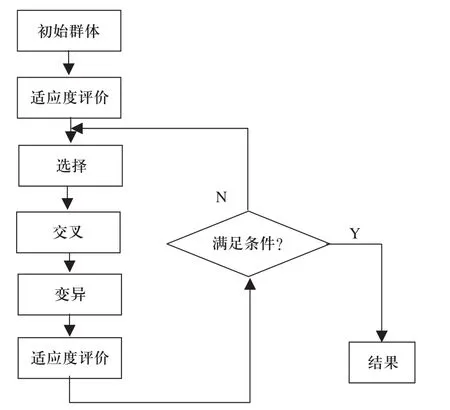
图1 标准遗传算法流程图

由图1可见，初始群体是遗传算法的第一步，初始种群的分布状态不仅直接关系到遗传算法的全局收敛性，还影响算法的搜索效率，所以对初始种群进行科学合理设定是应用遗传算法进行寻优计算的一个重要问题。

1 需求解的实际模型

在铁路客运领域，铁路企业为实现客运总收益最大化，在基于旅客需求预测的前提下可以建立以下一种多区间多票价的座位控制模型。

式中，AKT为FODF使用区间的矩阵，矩阵的列为一个FODF所包含的区间，akt为第t个FODF使用第k区间，否则akt＝0；

ck为第k个区间的列车的容量，C为全部ck组成的K维列向量；

st为第t个FODF的座位控制数，也就是决策变量，S为由全部st组成的t维列向量；

Rt为第t个FODF的收益。

该模型是一个随机规划模型，对于这种约束优化问题，可以使用遗传算法进行求解。

2 初始种群算法

对于该模型，如果使用产生随机数的方法来得到足够数量的初始种群，将大大增加算法的运算时间，而且由于传统GA的初始种群是随机选取的，初始种群的覆盖空间具有很大的不确定性，如果初始种群空间不包含全局最优解的信息，而遗传算子又不能在有限的进化代数内将覆盖空间扩延到全局最优解所在的区域，那么过早收敛就不可避免的[6]。本文采用以下方法得到初始种群。

定义1：随机产生一个个体，若该个体满足约束条件，则该个体称为可行个体，若该个体不满足约束条件，则称该个体为非可行个体[1]；

定义2：最初的可行个体的全体称为初始种群，个体的数量称为种群规模[1]；

设ai和bi分别为决策变量xi的取值上限和下限，Xi为第i个初始个体：

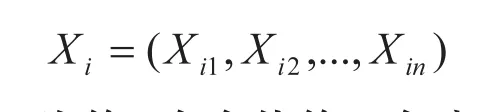
式中：Xip为第i个个体第p个分量的初始值，p＝ 1, 2, ,n。

若令rip为与第i个初始个体第p个分量相对应的在[0, 1]区间内服从均匀分布的随机数，X1为一个已知初始可行个体，它满足规划模型中的约束条件。

初始种群规模为m，于是可按下式随机产生一个初始个体X2：

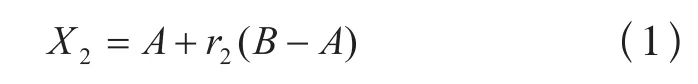
其中：检验新生成的X2是否满足约束条件，若满足则生成新的初始个体X3，若不满足则重复执行式（2）直至X2成为可行个体。

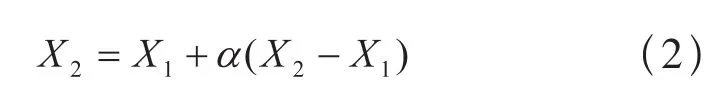
式中 为收缩系数，0≤ ＜1，一般可取0.5。

设x1p为X1的第p个分量，x2p为X2的第p个分量，其中p＝1, 2, ,n，为X2的第p个分量经过式（2）第k次迭代（即重复执行式（2）k次）后的值，则有

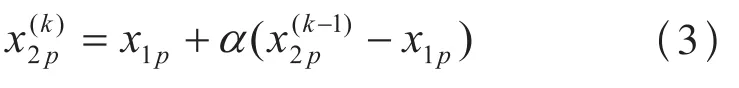
又因为

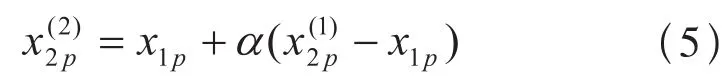
将式（4）代入式（5）中可得

设

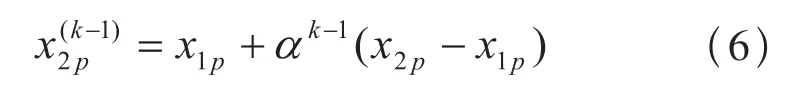
将式（6）代入式（3）中可得

由数学归纳法可知对于k＝1, 2, ，式（7）恒成立。

因为0≤ ＜1，当x2p≠x1p时，下述两式成立。

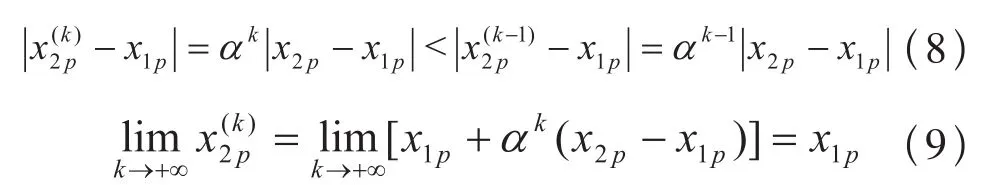
式（8）说明，当式（2）重复执行时，将使X2中的各分量的值不断地向X1中对应的各分量的值靠近。

式（9）说明，当式（2）重复执行时，将使X2中的各分量的值不断地向X1中对应的各分量的值无限地靠近。在一定的精度要求下，当与x1p的差距在精度要求的范围内时，可以令＝x1p。

若x2p＝x1p，当式（2）重复执行时，由式（7）可知，将始终等于x1p。

综上所述，若新生成的X2仍不满足约束条件，则对其重复执行式（2），使X2中的各分量的值不断地向X1中对应的各分量的值靠近。在一定精度要求下，可以经过有限次迭代，最终使X2中的各分量的值等于X1中对应的各分量的值。

通过上述算法，在X2向X1靠拢的过程中，X2有可能成为X1以外的其他可行个体，也有可能最终成为X1。当X2成为X1时，为了保证初始种群个体的多样性，可以按（1）再重新生成 ，再用式（2）重新迭代。

事实上，如果取 ＝0.5，我们可以认为用式（2）进行一次迭代后的新X2是X1与原X2连线的中点，如图2所示。

X2产生后，再产生X3，采用与X2同样的方法进行处理，最终能够产生m个初始可行个体。

对于本文的多区间座位控制模型，每个决策变量的取值范围均可以设定为[0, C]，其中C是列车的容量。根据边际期望座位收益方法分析，一般座位数量不会与需求量偏差很大，所以编码时对于每一个决策变量St只取[0,t+ 3t]之间的值，这样将会缩小搜索空间的范围，减少运算时间。

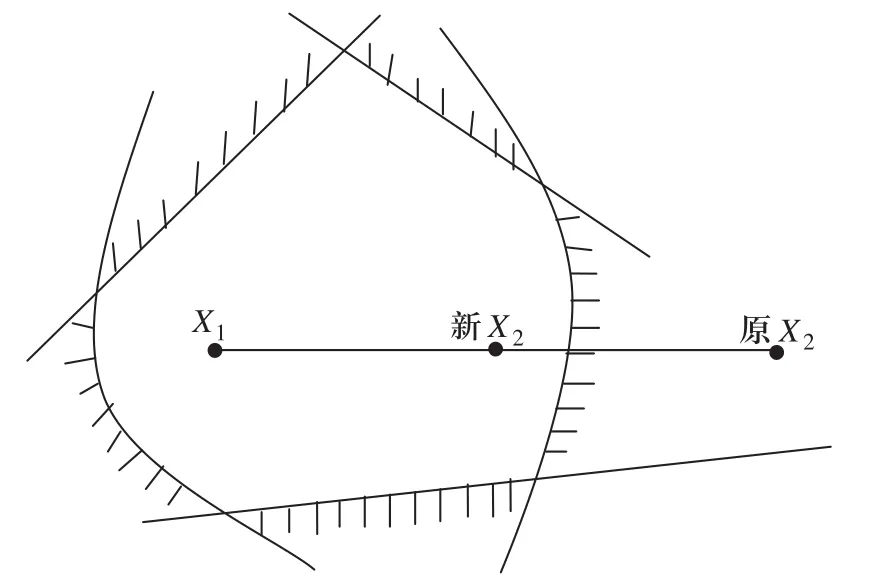
图2 X1与原X2和新X2之间的关系

对于本文的多区间座位控制模型，我们知道零向量是一个初始可行个体，可以将X1定义为零向量。但为了提高算法的收敛速度，对于第一个初始可行个体，可以采用如下方法自动获得。

我们知道，对于X1中第p个分量x1p所对应分布的p和p均为正数，其中p＝1, 2, ,T，因此若X1还不是可行个体，重复上述作法，可以使每一分量均逐渐向0靠拢，能够保证在有限迭代次数内使X1成为零向量，因此重复上述做法必然使X1成为可行个体。当X1成为可行个体后，再按照上述产生初始种群的方法产生其他初始可行个体。

3 算例

以2区间5种票价结构为例，初始种群规模设定为300。所有决策变量取值均在[0,1020]区间内。按随机产生初始种群的方法和本文所用的方法分别进行计算，得到表1所示的结果。

表1 两种方法的运行时间

4 结束语

实践证明，采用该初始种群算法可以有效地缩短求解该模型的时间。同时，该算法也可以应用到其他类似问题的求解中。

[1] 王福林,吴昌友,杨辉.用遗传算法求解约束优化问题时初始种群产生方法的探讨[J].东北农业大学学报.2004, (5).

[2] 田延硕.遗传算法的研究与应用[J].电子科技大学.2004.

[3] 张秀敏.我国铁路客票折扣销售研究[J].西南交通大学.2005[4] 高强, 朱金福, 陈可嘉.航空收益管理中多航段舱位控制模型[J].交通运输工程学报.2005, (4).

[5] 刘昌贵, 但斌.基于蒙特卡罗仿真技术的随机型库存决策方法[J].重庆大学学报(自然科学版).2006, (2).

[6] 何大阔, 王福利, 贾明兴.遗传算法初始种群与操作参数的均匀设计[J].东北大学学报(自然科学版).2005, (9).

[7] Chatwin R.E.Optimal Airline Overbooking.Ph.D.thesis.Department of Operations Research.Stanford Unicersity Palo Alto CA.1992.

[8] Sun X..Airline Yield Management.A Dynamic Seat Allocation Model.Master’s thesis Faculty of Commerce.University of British Columbia.1992.

[9] Shaykevich.Airline Yield Management.Dynamic Programming Approach Master’s thesis.Department of Operation Research.University of North Carolina.Chapel Hill, NC.1994.