基于压缩传感的超分辨率红外成像研究*
池小梅 马建伟 黄景涛
(河南科技大学电子信息工程学院)
基于压缩传感的超分辨率红外成像研究*
池小梅 马建伟 黄景涛
(河南科技大学电子信息工程学院)
为解决红外图像系统复杂度与成像分辨率之间的矛盾,采用压缩传感(compressive sensing, CS)理论对红外成像系统进行研究。通过对原始红外图像进行稀疏化,构造基于高斯随机噪声的测量矩阵,实现对目标的压缩感知,以较少数目的测量信号表示目标,获取目标的稀疏表达,基于对目标的稀疏表达,构造基于正交匹配追踪的重构算法对目标信号进行重构,实现以较少的测量信号构造较高分辨率的图像。在几种典型红外目标图像上的分析表明,压缩传感理论可实现对目标的超分辨率成像,以较低分辨率的传感器获得较高分辨率的目标信息,重构出的目标红外图像与相应高分辨率传感器所获得的图像之间误差较低。
压缩传感;红外图像;重构;测量矩阵;正交匹配追踪
1 引言
红外成像由于具有环境适应性好、作用距离远、隐蔽性好等特点,在军事领域有着广泛的应用,随着红外成像技术自身的发展,越来越多地应用于电力、石化、消防、医疗等民用领域。红外图像的高效获取和传输是一项极为重要的技术。随着技术进步和系统复杂性的提高,应用领域对红外成像质量的要求也不断提高,目前的主要方法是通过采用高分辨率的红外成像设备获取目标的高分辨率图像信息。为了方便传输、存储和处理,往往需要对所获取的高分辨率图像进行压缩处理,实现压缩的前提是信号本身具有一定的稀疏性,传统的红外图像处理过程是由高分辨率的成像设备获取目标信息,研究采用适当的压缩算法对所获取的红外图像进行压缩处理。压缩传感理论的出现为红外成像系统提供了新思路,其思想是将传感采样过程与压缩编码过程融合在一起,直接获取目标的结构信息;通过对所获取稀疏信号的重构,获取目标的高分辨率图像信息,Candes和Tao等建立了压缩传感的理论基础[1-2]。
压缩传感理论自出现以来,受到了广泛关注,在图像处理方面有着良好的应用前景。范晓维等采用分块技术对压缩传感过程进行了研究,提高了算法的处理速度[3];方红等研究了基于亚高斯的随机投影的图像重建方法[4];Chan等研究了单像素太赫兹成像系统,对目标进行快速成像[5];Duarte等在实验室实现了单像素成像系统[6];Herman等研究了压缩传感在雷达成像系统中的应用[7];Lustig等基于压缩传感理论研究了MRI快速成像问题[8]。本文针对红外成像问题基于压缩传感理论进行研究,探索超分辨率红外图像的获取方法。
2 压缩传感原理
自然信号大多具有内在稀疏性,这使我们可以对信号进行压缩处理,传统的信号处理方法是先根据Shannon采样定理采集信号,然后构造压缩算法对数据进行压缩处理,压缩传感的思想是直接将压缩和采集两个步骤融合为一个过程,直接采集稀疏信号,并基于稀疏信号进行原始信号的重构。压缩传感理论主要包含信号的稀疏表达、测量及重构三个环节。
2.1 信号的稀疏表达
实际物理信号往往为随时间变化的物理量,在时域内的信号f(t)可投影到一个正交空间内,表示为一组正交基的线性组合,即

2.2 压缩传感
对可压缩信号f(t),压缩传感理论指出,可以直接获取信号f的稀疏表达的传感矩阵(sensing matrix)。传感矩阵在什么条件下才能够由测量信号y重构出原始时域信号f是一个关键问题,Candes和Tao给出了传感矩阵需满足的等距约束性条件(restricted isometry property, RIP)[1],且此时,原始信号f可通过求解一个l0优化问题得到精确重构,即
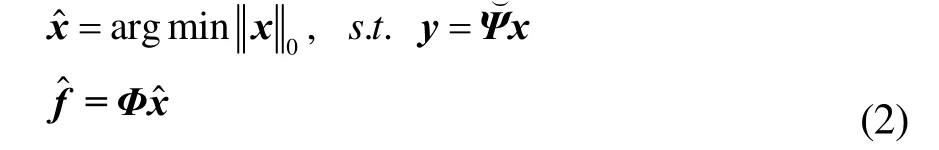
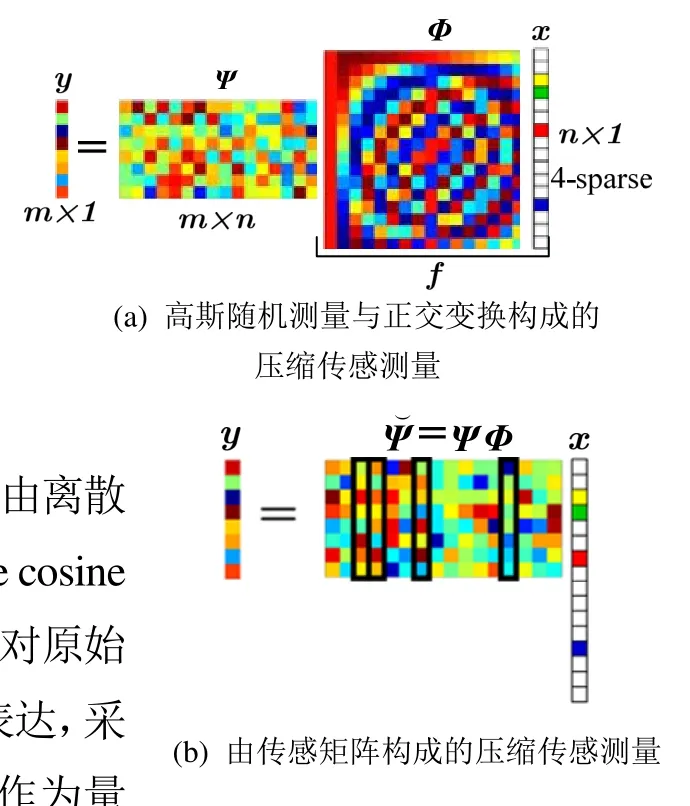
图1 压缩传感原理
2.3 信号的重构
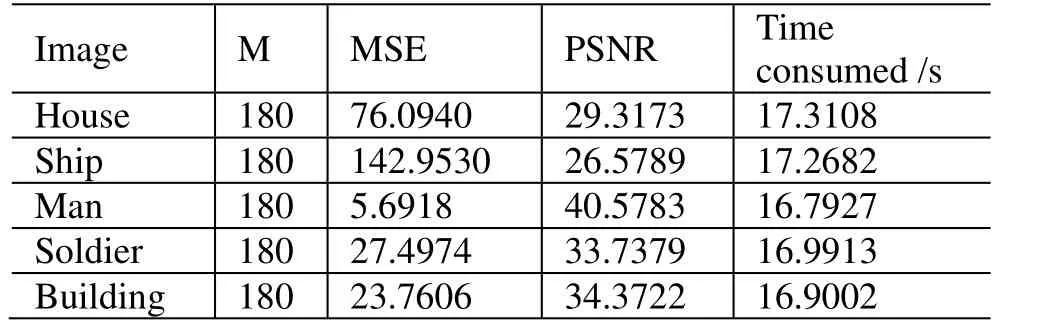
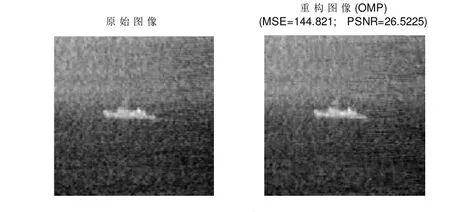
如上文所述,压缩传感的前提是信号具有稀疏性,可以在某一正交变换下进行稀疏表达,进而构造测量矩阵实现对稀疏信号的测量,获取测量信号y。能否由测量信号完美重构出原始信号f是一个关键问题。理论证明表明,对于一个K-sparse信号f,传感矩阵满足约束等距性条件的情况下,测量信号y的长度m≥cKlog(n/ K)时,在很大概率下能够由m< 式(2)是一个组合优化问题,直接求解存在一定困难,为此,可将其转化为一个等价的L1优化问题进行求解。以L1范数代替L0范数,问题(2)可转化为如下等价问题: 实际应用中允许存在一定的重构误差,问题(3)中的约束条件可放松为 正交匹配追踪算法(orthogonal matching pursuit, OMP)是信号重构的一种有效方法,属于一种贪婪搜索方法,在随机传感矩阵中不断搜索与稀疏信号匹配度最高的分量,最终在随机传感矩阵˘Ψ中找到K个与信号稀疏表达相对应的列向量,由此对原始信号进行重构,如图1(b)所示。该方法适合于低维小尺度信号的重构,对于大尺度、含噪声的信号,常用该算法重构效果较差,下面的实例分析也证实了这一点,本文OMP算法对红外图像进行压缩传感重构。 红外成像系统由于具有受光照影响小、可全天候工作的特点,在军事、工业、消防、电力等诸多行业有广泛用途。对红外图像质量的要求也越来越高,目前高分辨率的红外图像主要依靠高精度、高可靠性的传感器获得,以红外热像仪为代表的红外成像系统应用广泛,但成本较高。传感器阵列的增大带来很多技术问题,压缩传感理论的出现为超分辨率图像的获取提供了理论基础,可用较低像素的热像仪获取较高分辨率的图像信息。 本文对红外图像从稀疏表达、测量矩阵的选择、重构算法的构造等方面进行研究,以建筑物、战场人物、船只等典型场景红外图像进行分析处理,原始图像分辨率为256×256的灰度图像,灰度值在0~255之间。基于小波变换对原始图像进行稀疏表达,通过稀疏表达估计出原始信号稀疏度K,基此确定量测信号维数M,具体如表1所示。 表1 典型场景红外图像压缩传感结果 在Image、House、Ship、Man、Soldier、Building等几幅典型场景红外图像上的压缩传感及图像重构如图1~图5所示。基于压缩传感理论对信号进行稀疏表达,通过对稀疏信号随机投影得到其低维测量y,由测量值y直接通过OMP算法重构原始图像。原始红外图像的稀疏化采用离散小波变换(discrete wavelet transform,DWT),本文采用Symlets4作为小波母函数,分解层次根据图像分辨率确定,由于上述几幅典型场景的红外图像分辨率均为256×256,分解层次最小为4,最大为8。随机投影矩阵则采用高斯随机矩阵,如图1所示。得到目标信息的测量值后,通过OMP算法实现对目标信息的重构,即重构原始红外图像,获取比测量值分辨率高的红外图像。 重构图像与原始图像之间呈现较小的误差,在红外图像Man上的均方差(mean square error, MSE)只有5.69左右,其重构图像信噪比达40.5783;在图像Ship上的均方差则较大,达142.9530,图像信噪比为26.5789,这是由于原始图像本身噪声水平较高。在各场景红外图像的重构图像均方差MSE及峰值信噪比PSNR如表1所示,由于测量矩阵为随机矩阵,因此,即使对同一图像,每次重构结果也不尽相同,表1中的结果为10次实验的平均值,图2~图6则是对每一场景在10次实验中随机选择的一组结果。 图2 House压缩传感传感效果 图3 Ship压缩传感效果 图4 Man压缩传感效果 图5 Soldier压缩传感效果 图6 Building压缩传感效果 红外成像系统在现代武器、电力、医疗、化工等领域应用越来越广泛,各应用领域对红外成像质量的要求也越来越高,目前主要解决方法是研制高分辨率、高灵敏度的红外成像设备,这意味着红外成像系统的复杂度越来越高,应用成本也随之增高,同时,传感器分辨率的提高使其获取的图像数据量越来越大,对数据处理系统的要求也随之提高。另一方面,多数图像具有大量的冗余信息,即信号本身具有一定稀疏性,需要在传输、存储等环节对其进行压缩处理,压缩传感理论的出现为缓和系统复杂性与红外图像质量之间的矛盾提供了有效途径,将压缩和传感两个环节有机融合,直接获取目标的一组测量信息,基于低分辨率测量信息重构出目标的高分辨率红外图像,实现少数传感器阵列获取高分辨率的红外图像。本文采用压缩传感理论对几种典型场景的红外图像进行了分析,结果表明,采用压缩传感理论,基于低维测量信息可有效重构出高分辨率目标红外图像,重构出来的图像与原始图像之间误差较小,图像的峰值信噪较高。为构造红外图像压缩传感成像硬件系统提供了基础。 [1] Candes, E. and T. Tao. Near-optimal signal recovery from random projections:Universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006. 52(12):5406-5425. [2] CANDES, E., J. ROMBERG, and T. TAO. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006. 59(8):1207-1223. [3] 范晓维,刘哲,刘灿.分块可压缩传感的图像重构模型[J].计算机工程与应用, 2009. 45(29):153-155. [4] 方红,章权兵,韦穗.基于亚高斯随机投影的图像重建方法[J].计算机研究与发展, 2008. 45(008):1402-1407. [5] Chan, W., et al.. A single-pixel terahertz imaging system based on compressed sensing[J]. Applied Physics Letters, 2008. 93:121105. [6] Duarte, M., et al.. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008(3):83-91. [7] Herman, M. and T. Strohmer. High resolution radar via compressed sensing[J]. IEEE Trans. Signal Processing, 2007. 57(6). [8] Lustig, M., D. Donoho, and J. Pauly. Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 2007. 58(6):p. 1182–1195. [9] Baraniuk, R. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007. 24(4):118-120,124. 池小梅,女,1979年生,浙江金华人,硕士研究生,主要研究领域为压缩传感、图像处理。 马建伟,男,1965年生,河南新郑人,博士、副教授,主要研究领域为系统控制、信号处理。 黄景涛,男,1977年生,河南汝州人,博士、副教授,主要研究领域为复杂系统控制、智能系统。 Research on Super Resolution Infrared Imaging by Compressive Sensing Chi Xiaomei Ma Jianwei Huang Jingtao (Electronic and Information Engineering College, Henan University of Science and Technology) To solve the conflict between complexity and image quality of infrared imaging systems, the theory of compressive sensing was applied to research the infrared imaging systems. The sparse representation was obtained by projecting the original infrared image to a special space. To position the sparse of the original image, a measure matrix was constructed based on Gaussian noise distribution, then a measurement with less elements of the target can be obtained. A reconstruction method based on orthogonal matching pursuit was used to reconstruct the original infrared image from the measurement. So far super-resolution can be implemented by the sensor with low resolution. The results on several typical infrared images show that super-resolution imaging can be realized by compressive sensing theory, high resolution information can be sampled by low resolution sensors, and the mean square error was low between the reconstructed image and original image. Compressive Sensing; Infrared Image; Reconstruction; Measurement Matrix; Orthogonal Matching Pursuit
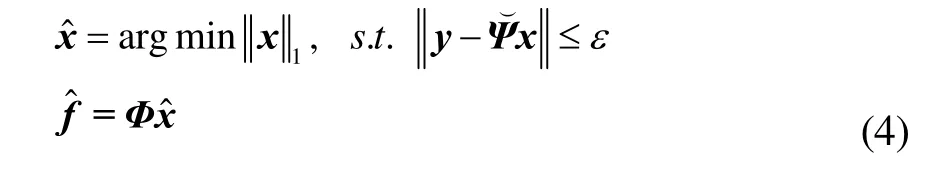
3 基于压缩传感的红外图像处理




4 结论

