重力坝坝踵应力控制标准的研究
杨清平,李俊杰
(大连理工大学,辽宁 大连 116023)
随着计算机技术的飞快发展,有限元计算方法也得到了迅猛的发展,已经广泛的运用在各个领域。但用有限元方法求解重力坝坝踵应力时,得不到准确解,应力在此失真,即随网格的不同,应力在坝踵区有明显的差别。然而,重力坝设计规范是根据材料力学解出的,有限元方法没有相配套的设计标准。加之,影响重力坝坝踵应力的因素很多,例如基岩特性、坝体材料分区、地基与坝体弹模比、扬压力等,所以到目前为止,重力坝坝踵应力控制标准一直没有得到很好的解决。在阅读文献[1]、文献[2]的基础上,作者做了一些有意义的工作。由于影响因素众多,本文的计算荷载仅考虑水平水压力和坝体自重,为进一步研究其他工况打下一定的基础。在此引入坝踵主应力区相对宽度的概念,定义坝踵主应力区相对宽度brL为坝踵主应力区宽度b与坝体底宽B的比值,用公式表示为brL=b/B×100%。
1 计算工况和网格剖分
1)坝高。为了考虑在不同坝高的情况下,网格剖分的不同对坝踵应力分布规律的影响,本文计算了几种坝高的重力坝,其坝高分别为80,110,160,190 m。其典型断面和计算水位如图1所示。
2)坝体下游边坡。为了考虑在不同坝体下游边坡的情况下,网格剖分的不同对坝踵应力分布规律的影响,对于每种坝高分别进行了3种边坡的计算,3 种边坡的大小分别是 1∶0.70,1∶0.75,1∶0.80。
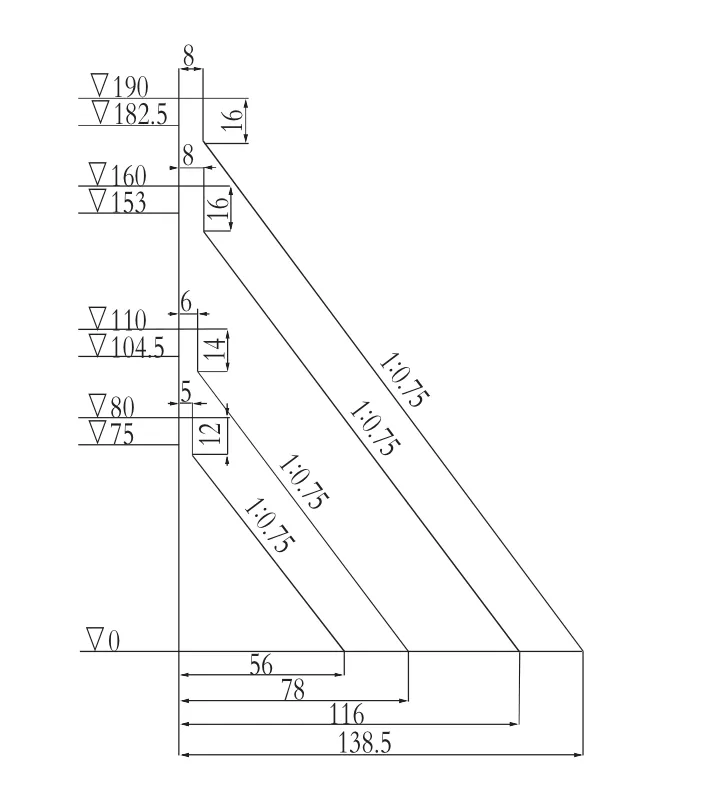
图14种坝高的典型断面和计算水位图
3)坝基与坝体弹模比。为了考虑在不同坝基与坝体弹模比的情况下,网格剖分的不同对坝踵应力分布规律的影响,对每种坝高、每种边坡计算了3种弹模比的计算,3种弹模比大小分别是0.5,1.0,2.0。对于160 m 的高坝进行了6种弹模比的计算。6 种弹模比分别为 0.5,1.0,2.0,4.0,8.0,10.0。
4)地基剖分区域。为了使计算的结果尽可能的接近实际的情形,在剖分坝基时,坝基上下游剖分长度分别为3倍的坝高,坝基剖分深度为三倍的坝高。
5)地基及坝体网格加密区域。根据以往作的研究表明,一般情况下,重力坝坝踵主拉应力区的相对宽度约为21%,主拉应力区的相对高度约为7%。基于这些结果,坝踵处加密区域采用水平向为坝底宽度的30%,加密区域竖向高度约为坝高的10%。并且,与坝踵及建基面相邻的地基也进行了加密。
6)网格尺寸。由于有限元方法在分析应力奇异点时,结果失真,网格剖分的不同对结果的影响很大,因此本文在计算时把加密区域的网格分为28组,便于分析网格对应力奇异点的影响。由于数据量很大,本文选用160 m高的坝,网格剖分数据见表1。

表1160 m高坝网格剖分信息
2 计算参数
由于工况很多,本文采用线弹性的有限元模型进行计算,取坝体混凝土容重γ=23544 N/m3,泊松比μ=0.17,弹性模量Ed=2×1010Pa。取地基容重 γ=0 N/m3,泊松比 μ=0.20,弹性模量 Ef=4×1010Pa。坝体与地基剪切模量按照公式转换。
3 网格对坝踵主拉应力分布规律的影响
通过对不同坝高、不同下游边坡、不同地基与坝体弹模比的情况,分别进行了28组网格的计算,计算结果表明:不同情况下,网格对坝踵主拉应力的影响表现出一致性和稳定性。
对于110 m坝、190 m坝,选取下游边坡为1∶0.75、地基与坝体弹模比为1.0的5组网格的计算结果分别绘于图2和图3中。

图2110 m坝五组网格计算的沿坝建基面相对宽度的变化曲线
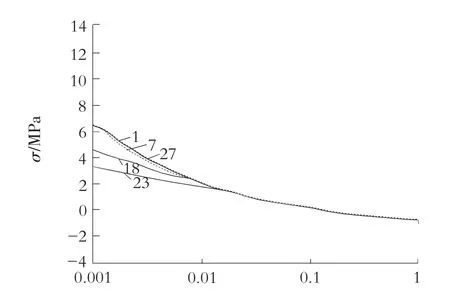
图3190 m坝五组网格计算的沿坝建基面相对宽度的变化曲线
由图2和图3可以看出,在沿建基面距坝踵一定范围之外,网格剖分的不同对主应力的分布规律的影响非常小,基本可以忽略不计。在沿建基面坝踵主拉应力区的范围内,网格剖分的不同对主拉应力的大小和分布有一定的影响,在沿建基面距坝踵较小的范围内,主拉应力随网格剖分的不同有较大的差异(见表2)。从表2中可以看出,对于110 m高坝,7号网格在坝踵处主拉应力值为5.31 MPa,23号网格在此处的主拉应力值为1.45 MPa,两者相差了3.86 MPa;对于190 m高坝,1号网格在坝踵处主拉应力值为13.48 MPa,23号网格在此处的主拉应力值为3.14 MPa,两者相差了10.34 MPa。如果用沿坝建基面相对宽度来度量,从图1和图2中也可以看出在距坝踵的相对宽度值大约为7%的范围以外,网格剖分的不同对主应力的分布规律的影响非常小;在距坝踵的相对宽度值大约为7%的范围以内,主拉应力随网格剖分的不同有较大的差异。网格剖分的越细,主拉应力在坝踵处的值也越大,其应力递减梯度也越大。但网格剖分的不同对坝踵的主拉应力区相对宽度影响较小。也就是说,坝踵的主拉应力区相对宽度相对于坝踵网格剖分的不同是较为稳定的。
4 重力坝坝踵应力控制标准的研究
通过以上的分析,可以知道:网格剖分的不同对主应力的大小和分布沿整个建基面都有不同程度的影响,从坝踵到坝趾这种影响依次减弱,不同网格之间的误差在距坝踵较近的区域内递减很快。为了研究这个问题,取80,110,160,190 m等4种不同的坝高、3种不同的地基与坝体弹模比0.5,1.0,2.0、下游边坡1∶0.75多种不同网格的计算结果来进行分析,为了研究方便,定义主应力σ1的绝对误差为:在沿建基面距坝踵等距的地方,不同网格计算的主应力值σ1i与这些主应力平均值的差值的最大值,用公式表示为,其中ea为主应力σ1在建基面某处的绝对误差,在这里,n=28。定义主拉应力σ1相对误差为:主应力σ1绝对误差与主应力平均值的比值,用公式表示为,其中,er为主应力σ1在建基面某处的相对误差。
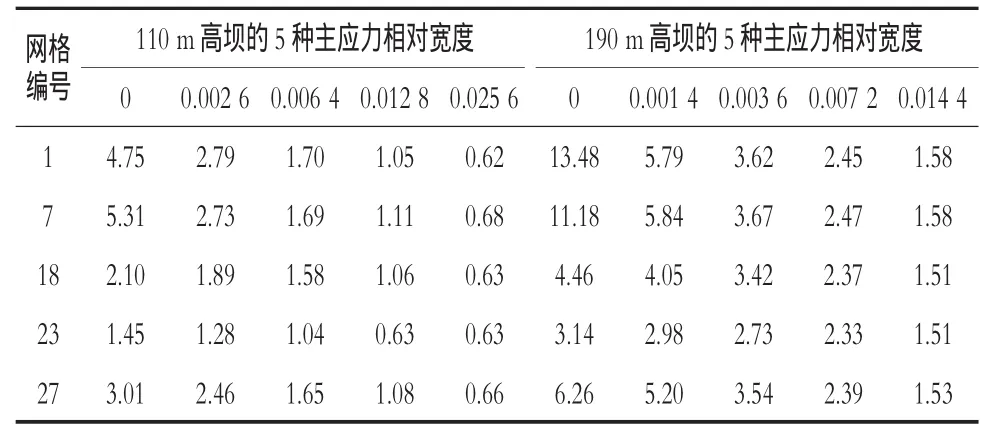
表2110,190 m高坝在不同网格下主应力相对宽度和对应的值
采用相同坝高,相同地基与坝体弹模比的不同网格之间的主应力σ1的相对误差来研究重力坝坝踵应力控制标准。本文取了7种主应力σ1的相对误差作为控制标准和他们对应的建基面相对宽度来分析不同网格之间的差距,其结果见表3。
从表3中数据可以得出:
1)地基与坝体弹模比的不同对网格剖分的影响。对于相同的坝体,不同的网格,在相同的主应力σ1的相对误差的控制下,地基与坝体的弹模比越大,大于该项误差的主应力σ1的分布区域越小。地基与坝体的弹模比越小,大于该项误差的主应力σ1的分布区域延伸的越远。甚至沿整个建基面都大于该项误差。也就是说,随着地基与坝体弹模比的增大,网格剖分的不同对主应力沿建基面的分布和大小的影响相对减弱。
2)坝高的不同对网格剖分的影响。对于相同的地基与坝体的弹模比,不同的坝高,在相同的主应力σ1相对误差的控制下,坝体越高,大于该项误差的主应力σ1的分布区域沿建基面相对宽度越小,并且沿整个坝基的主应力σ1的分布是很稳定的。也就是说:坝体越高,网格剖分的不同对主应力σ1沿建基面的分布和大小的影响相对减弱。

表312种工况,7种主应力σ1的相对误差控制值计算得出的坝踵沿建基面的相对宽度
3)局部条件下的应力控制标准。通过以上2点的分析,得出一些局部坝体的定量标准:在地基与坝体弹模比较小、坝高较小的情况下,网格剖分的不同对坝踵的主应力σ1的大小和分布影响越大,很难确定坝踵的应力控制标准。对于地基与坝体模比大于1.0、坝高大于80的坝体。其可以采用不同网格之间的5%的主应力σ1的相对误差作为控制标准,此时,应力失真区沿建基面的相对宽度可以认为小于2%。
5 结语
由于影响坝体的影响因素、计算工况很多,所以计算量很大。本文是基于平面四边形单元、考虑部分影响因素探讨了重力坝坝踵区的应力控制标准,成果的整理和分析相对比较粗糙,关于重力坝有限元的强度控制标准,还需要做大量后续工作。
[1]王春涛,练继建.重力坝坝踵应力集中问题的有限元法研究[J].水利水电技术,2003(5):10-12.
[2]赵代深.重力坝有限元计算网格剖分与应力控制标准问题[J].水利学报,1996(5):37-43.

