面向移动终端的统计机器翻译解码定点化方法

李 响，徐金安，姜文斌，吕雅娟，刘 群

(1. 中国科学院 计算技术研究所 智能信息处理重点实验室，北京 100190;2. 北京交通大学 计算机与信息技术学院，北京 100044)

1 引言

作为自然语言处理领域一项具有挑战性的技术，统计机器翻译为克服语言障碍提供了一个解决方向。与此同时，嵌入式硬件的快速发展使移动终端运行复杂的统计机器翻译系统成为可能。

最近，随着机器翻译研究的不断深入，基于语料库的自然语言处理技术的发展使现实环境中的语音翻译成为可能，一些多语言语音翻译系统已经出现。可以预见，在未来的国际交流和经贸交往中，具有高效统计机器翻译功能的移动终端将会得到广泛利用，将成为相关人士的必备工具。

目前，商用移动终端上的机器翻译主要采用基于规则的方法，这种方法需要针对源语言和目标语言设计翻译规则，而规则自动获取难度大，主要依靠人工编写，系统的造价和成本高，仅仅适用于受限的领域，系统不易扩充、更新和维护；然而，基于统计的机器翻译不依赖语言学知识，能够很快的实现多语言互译，但翻译模型庞大，翻译计算耗时长，消耗系统资源较多[1-2]。

近年来，嵌入式硬件性能的不断提升使移动终端运行统计机器翻译成为可能，然而，统计机器翻译需要大量的浮点运算，无浮点运算单元的中低端嵌入式处理器影响了翻译速度。另一方面，面向移动终端的语音翻译也面临同样问题。对此，本文提出了将统计机器翻译解码运算定点化的方法。与统计机器翻译的浮点解码运算相比，利用定点实现解码运算可以降低对计算资源的需求，获得更好的翻译性能。实验结果表明，在保证同等翻译质量的情况下，本方法可以有效地提高统计机器翻译在移动终端上的翻译速度。

本文在第2节简要介绍了统计机器翻译系统，第3节介绍了计算机内部数据的表示方法，第4节详细阐述了利用定点处理浮点运算的解码器实现，第5节是实验结果，第6节是对本文的总结和对未来的展望。

2 统计机器翻译系统

本文以Xiong et al.的Bruin系统[3]为实验系统，重新实现了一个以定点运算替代浮点运算的统计机器翻译解码器。

Bruin系统主要由以下三个特征：

(1) 括号转录语法(BTG)[4]，并用对数线性形式的多种特征对规则赋予权重；

(2) 基于最大熵的调序模型，其特征通过双语训练集自动学习；

(3) 采用Beam Search的CKY类型的解码器。

下面，我们主要介绍通过BTG对翻译过程的实现，如下式所示。

规则(3)将源短语x翻译为目标短语y，并生成一个块A，规则(1)和(2)以正向或反向顺序将两个连续的块合并为一个更大的块。

Bruin采用对数线性模型计算规则概率，从而构建一个BTG。对于规则(1)和(2)，指定的概率定义如公式(4)。

(4)

其中，Ω表示通过最大熵调序模型得到的A1和A2的重调序得分，λΩ表示Ω的权重；ΔPLM(A1,A2)表示根据调序结果得到的两个块的语言模型分数增量，λLM表示ΔPLM(A1,A2)的权重。

规则(3)的概率定义如公式(5)。

Prl(A)=p(x|y)λ1·p(y|x)λ2·plex(x|y)λ3

·plex(y|x)λ4·exp(1)λ5

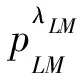
(5)

其中p(·)表示短语双向翻译概率，plex(·)表示词汇化双向翻译概率，exp(L)表示短语惩罚，exp(|y|)表示单词惩罚，λs表示特征权重，通过多种加权特征概率获得规则概率。

3 计算机内部的数据表示

下面主要介绍与本文密切相关的浮点与定点数据在计算机中的表示方法。

3.1 浮点数据表示方法

在广泛采用的IEEE-754浮点标准中[4]，浮点数是将特定长度的连续字节分割为特定长度的符号域S，指数域E和尾数域M，其尾数域M由小数部分和一个隐含的小数点组成，同时指数域E的基数2也是隐含定义的。

IEEE-754标准明确定义了32位单精度浮点和64位双精度浮点两种基本浮点数据类型的表示方式以及运算法则。

单精度浮点格式表示如图1，其中N共32位，其中S占1位，E占8位，M占23位。

图1 单精度浮点格式

双精度浮点格式表示如图2，其中N共64位，其中S占1位，E占11位，M占52位。

图2 双精度浮点格式

3.2 定点数据表示方法

在计算机中，定点数据既可表示整数也可以表示小数。定点数是将特定长度的连续字节分割为特定宽度的符号域S，整数域IWL和小数域FWL，如图3所示[6]，当设定隐含小数点在最低位时，定点数据只能表示整数，反之，则可以表示小数。

图3 定点数据类型的表示形式

定点数据类型约定了参与运算的数据的小数点隐含在某一固定位置上，而在对小数点位置做出选择后，运算中的所有数均应统一为定点数据类型，在运算中不再考虑浮点数问题。

4 解码器运算的定点化实现

由于无浮点运算单元的嵌入式处理器本身不提供对浮点运算支持的寄存器和指令集，即使可以通过编译器实现浮点运算，但这样会频繁产生CPU中断，增加了系统延迟，降低了运算效率。因此，为了提高无浮点运算单元处理器运行统计机器翻译的解码速度，在此类嵌入式处理器上运行的统计机器翻译解码算法中，我们需要用定点数据类型来表示解码算法中的浮点类型及实现相应运算，在保证一定翻译质量的情况下，提高解码器的翻译速度，即解码器运算的定点化实现。

4.1 数据类型的格式转换

数的定标是通过开发人员来决定小数点在定点数据中的位置，从而确定实数的范围和精度。Q格式是一种常用的定标格式，其小数部分位数已经设定，例如，Q15表示该定点数有15位小数。因此，针对移动终端统计机器翻译解码，我们采用Q格式定点数来处理浮点数据和运算。可以通过改变定标值，使程序更加灵活，适应不同的处理器和统计机器翻译解码器。

将一个基本浮点数据转换为Qn格式的W位定点数据所执行的操作如下：

(1) 获取存储浮点数的连续字节内容于一个W位整型变量；

(2) 根据IEEE-754标准对基本浮点数据的存储格式定义，获得浮点数的符号，指数和尾数；

(3) 根据指数对尾数进行缩放，然后根据Qn格式，将缩放后的尾数转换为相应的定点数，并采用截断方式处理超过定点字长的位。

最后，我们以小数1.123 4为例说明其转换方式，其单精度浮点数存储格式如图4。

图4 定点数值类型表示形式

其中：

符号：S=0，表明该浮点数为正数；

指数：E=0x7F，实际指数E′=E-Bias=127-127=0；

尾数：M=0x8FCB92，实际尾数M′=M|0x800000=0x8FCB92。

下面采用Q8格式的16位整数类型变量替换浮点数，则小数1.123 4的定点存储格式如图5。

图5 实数1.123 4的Q8格式定点存储格式

4.2 定点化类

为了在SMT系统中采用不同精度定点运算，我们用执行效率更高的C++设计了一个定点化类Fixed_SMT，该定点化类主要包含两个属性：整数域长度IWL和小数域长度FWL，通过这两个主要属性来调整实数的表示范围和精度，同时，该类对+，-和×等相关运算进行了重载定义，使其满足解码运算需求。这样通过定点类对象的运算可以模拟浮点运算。

4.3 解码器定点化方案

用定点运算模拟浮点运算是整个解码器定点化过程中的重点，需要预先知道解码过程中参与浮点运算的浮点类型变量的范围，然后用一定精度的定点类型变量来表示它们，再通过定点运算模拟实现原来的浮点运算。

下面，我们介绍对Bruin系统解码器的定点化工作。

(1) 由于解码器采用的语言模型直接调用SRILM[7]接口，我们暂时无法实现其定点化，因此，我们仍然利用常规的浮点运算获得语言模型和翻译模型；

(2) 由于解码器使用了语言模型、短语惩罚等九个特征，并为每个特征赋予权重，并采用式(6)计算当前短语翻译评分，因而我们便对其中的特征值和权重值分别进行定点化。

(6)

图6为解码器的定点化的具体流程，通过分析解码过程涉及的浮点变量的运算范围和精度，设置定点类采用的Q格式，进而替代解码器的浮点变量和运算，实现定点运算模拟浮点运算。最后，我们要对模拟结果进行验证，从而调整定点格式设置以优化解码运算和翻译精度。

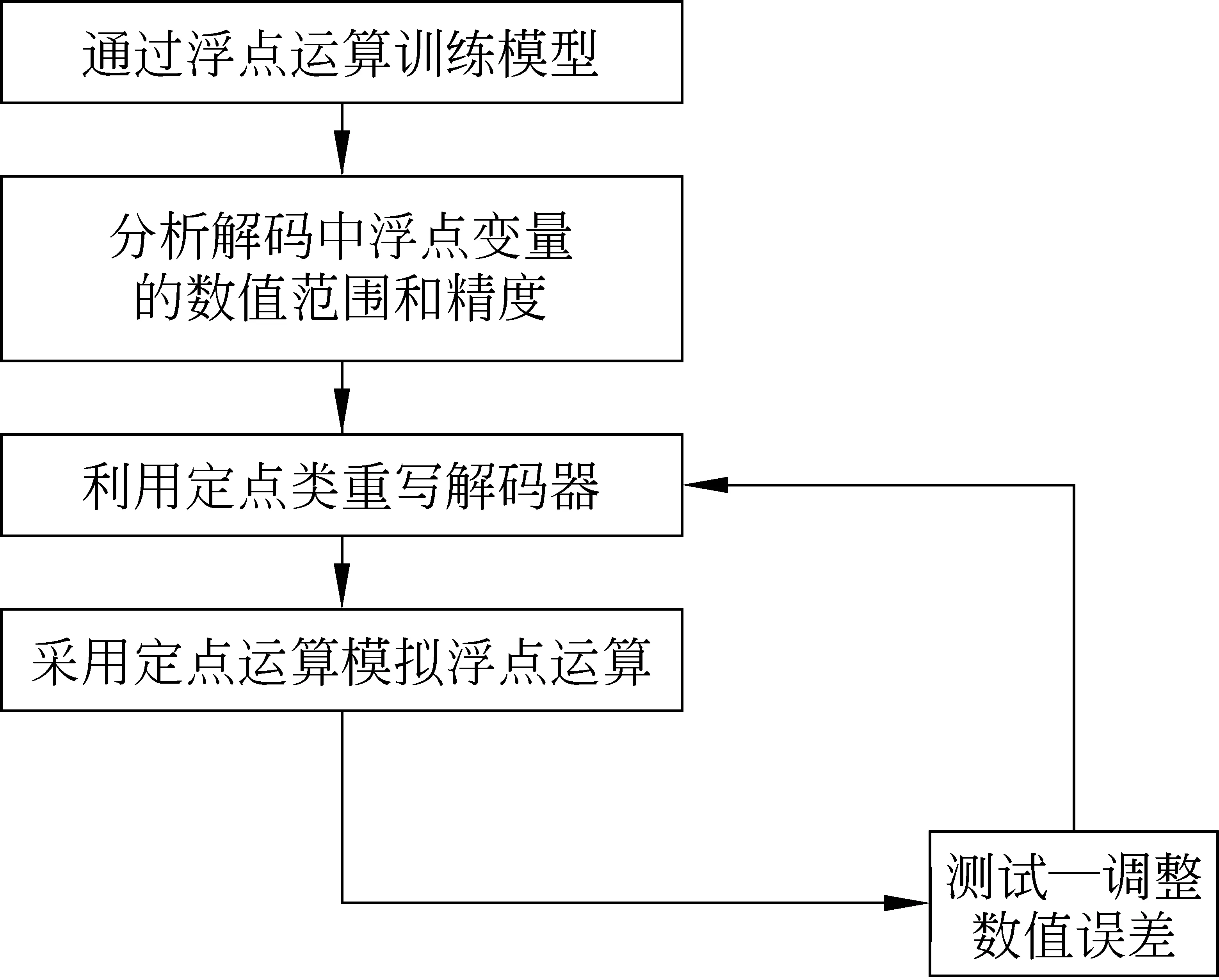
图6 解码器定点化流程

通过上述处理，定点运算在功能上完全和被替换的浮点运算一样，只是在精度上略逊于浮点运算。当把这样的替换应用到整个的解码器代码空间后，并且能保证翻译结果在允许的误差范围内时，相当于消除了所有的浮点运算，此时解码器也已经定点化。

5 实验

下面，我们将分别在PC和移动终端上进行定点解码器和浮点解码器的性能对比实验。

5.1 PC实验

本实验均是在汉英方向上进行，并且使用FBIS(共239K双语对)作为训练集，NIST 2002汉英测试数据作为开发集，NIST 2005汉英测试数据作为测试集。

我们使用SRILM工具包对训练语料的目标端训练了一个四元语言模型，并采用Kneser-Ney[8]平滑方法。同时，我们使用大小写不敏感的BLEU[9]来衡量翻译质量。

表1 PC实验平台配置信息

表2的PC实验结果表明，定点解码器可以保证较好的翻译质量，而速度稍慢于浮点解码器。可以预测，将定点解码器移植到无浮点运算单元的移动终端中，翻译速度将会有较大提升。

表2 PC实验结果

由于统计机器翻译系统对内存要求较大，限于硬件条件，我们采取在移动终端上对定点和浮点数值运算性能进行对比试验，间接验证我们的统计机器翻译定点化解码器的解码速度。

5.2 移动终端实验

我们在无浮点处理单元的移动终端中进行定点和浮点运算性能对比实验，分别对定点数值和浮点数值进行10 000 000次的循环运算，其中运算类型采用统计机器翻译解码中运算频率较高的乘法和累加运算。

由于实验采用的移动终端没有浮点处理单元，因此其浮点运算采用内核中非定义指令的异常中断处理方式，浮点指令被截获并由浮点模拟器模块来执行。

表4的实验结果表明，定点运算性能较浮点运算性能提高135.6%，从而可以间接验证，将本文设计的定点解码器移植到无浮点运算单元的移动终端中，将会有效提高统计机器翻译的解码速度。

表3 移动设备实验平台配置信息

表4 移动终端实验结果

6 总结与展望

近几年，统计机器翻译技术已经取得大量成果，进展迅速，实用性进一步提高，同时，由于嵌入式移动终端的广泛普及和硬件性能的提高，统计机器翻译可以在移动终端中得到应用。然而，由于大量的中低端低耗能的嵌入式处理器缺乏浮点处理单元，从而导致统计机器翻译速度较慢的问题。为了提高统计机器翻译在移动终端中的翻译速度，我们提出了解码运算的定点化方法。实验结果表明，本文方法有效地提高了统计机器翻译在浮点运算能力薄弱的移动终端上的翻译速度，同时保持了较好的翻译质量。

另外，本文提出的方法也适用于语音识别、语音翻译、图像处理等相关领域，具有较高的实用价值。

在以后的研究中，我们希望完成以下方面的工作：

第一，实现对SRILM训练语言模型的定点化，进一步提高移动终端中统计机器翻译性能；

第二，针对其他受限于浮点硬件的统计机器翻译系统模块，提出针对性的优化方法；

第三，针对iPhone，Android等移动平台，结合具体移动终端，利用我们的方法实现初步的统计机器翻译系统。

[1] 徐金安. 机器翻译展望[C]//2010海峡两岸信息科学与信息技术学术交流会议. 秦皇岛，2010：368-372.

[2] 刘群. 统计机器翻译综述[J]. 中文信息学报，2003，17(4)：1-12.

[3] Deyi Xiong, Qun Liu, Shouxun Lin. Maximum entropy based phrase reordering model for statistical machine translation[C]//Proceedings of the 21st International Conference on Computational Linguistics and the 44th annual meeting of the Association for Computational Linguistics，Sydney，Australia，2006：521-528.

[4] Dekai Wu. Stochastic Inversion Transduction Grammars, with Application to Segmentation, Bracketing, and Alignment of Parallel Corpora[C]//Proceedings of IJCAI 1995，Montreal，Canada，1995：1328-1334.

[5] ANSI/IEEE. IEEE Std 754-1985，IEEE Standard for Binary Floating-Point Arithmetic[S]. 1985.

[6] K-l Kum, J. Kang, and W. Sung. A floating-point to fixed-point C converter for fixed-point digital signal processors[C]//Proc. 2nd SUIF Compiler Workshop, 1997.

[7] Andreas Stolcke. SRILM—An Extensible Language Modeling Toolkit[C]//Proc. Intl. Conf. on Spoken Language Processing，2002：901-904 .

[8] Stanley F. Chen and Joshua Goodman. An empirical study of smoothing techniques for language modeling[C]//Proc. 34th ACL，1996：310-318.

[9] Kishore Papineni，Salim Roukos，Todd Ward et al. BLEU: a method for automatic evaluation of machine translation[C]//Proceedings of ACL 2002，2002：311-318.

[10] David Goldberg. What Every Computer Scientist Should Know About Floating-Point Arithmetic[J]. ACM Computer Surveys，1991， 23(1)：5-48.

[11] 张海滨，李挥. 基于S3C2410的WMA开源解码程序优化[J]. 计算机工程与设计，2009，30(1)：13-15.

[12] 曾微维，郑善贤，成钢. 基于统计的机器翻译在嵌入式系统上的实现[J]. 计算机系统应用，2009,18(9)：1-4.