多帧相参积累检测前跟踪方法✴

樊玲

（1.乐山师范学院物理与电子工程学院，四川乐山614004；2.电子科技大学电子工程学院，成都611731）

多帧相参积累检测前跟踪方法✴

樊玲1，2

（1.乐山师范学院物理与电子工程学院，四川乐山614004；2.电子科技大学电子工程学院，成都611731）

为了提高雷达对微弱目标的检测能力，提出了一种多帧相参积累的检测前跟踪（TBD）方法。通过对多帧时间内运动目标回波的分析，建立了相参积累的回波信号模型，其中目标回波出现距离单元走动和多普勒单元走动。利用目标回波的空-时相关性，采用速度匹配法和离散Chirp-Fourier变换（DCFT）联合估计目标径向速度、多普勒频率和调频斜率，补偿距离单元走动和多普勒单元走动，实现多帧时间内目标能量的相参积累。最后，采用仿真实验验证了信号模型的正确性和算法的有效性。

相参雷达；检测前跟踪；相参积累；速度匹配；离散Chirp-Fourier变换

1 引言

在低信噪比环境下检测和跟踪运动目标一直以来都是一个非常具有挑战性的研究课题。为了提高雷达对微弱目标的检测与跟踪性能，通过联合处理多帧原始数据，利用目标运动特性，沿目标轨迹进行能量积累，以实现同时检测和跟踪的检测前跟踪（TBD）方法受到了很大的关注。常用的TBD方法有基于Hough变换的方法［1］、动态规划TBD方法［2-4］和粒子滤波TBD方法［5-7］。这些方法对单帧回波数据进行相参处理，形成方位-距离-多普勒平面的幅度或功率输出，再在多帧的方位-距离-多普勒平面上采用TBD算法实现对目标能量的积累。也就是说，现有的TBD方法在多帧能量积累的过程中，只利用了幅度信息，而丢弃了相位信息，因此它们在多帧间实现了对目标能量的非相参积累。很明显，只利用幅度信息的非相参积累的效率低于同时利用幅度信息和相位信息的相参积累［8］。

基于上述分析，针对相参雷达系统，本文提出了一种在多帧时间内实现相参积累的TBD方法。首先分析了多帧时间内运动目标的回波，建立了多帧相参积累的信号模型。由于在多帧时间内，运动目标回波出现距离单元走动和多普勒单元走动，要实现相参积累必须进行运动补偿。运动补偿意味着要求已知运动目标的参数，而对于非合作目标，其参数是未知的，必须采用有效的算法对其进行估计。根据建立的相参积累回波信号模型，提出了联合采用速度匹配法和离散Chirp-Fourier变换（DCFT）的方法估计目标参数（径向速度、多普勒频率和调频斜率），补偿距离单元走动和多普勒单元走动，实现对多帧时间内目标能量的相参积累。最后，采用仿真实验验证了本文信号模型的正确性和所提算法的有效性。

2 回波模型

考虑一个电子扫描天线的相参雷达系统，该系统在连续的K帧时间内发射相参脉冲。由于天线的扫描，系统在每个方位单元发射M个脉冲，整个监视区域被分为Na个方位单元，系统对监视区域完成一次扫描的时间为TR，脉冲重复频率为Tp。因此，在K帧时间内，系统连续发射的相参脉冲数为N=K×Na×M。接收机序贯地接收回波，经去载频、滤波和采样后按图1所示的结构存储回波，回波在慢时间维上形成了一个连续的时间序列。

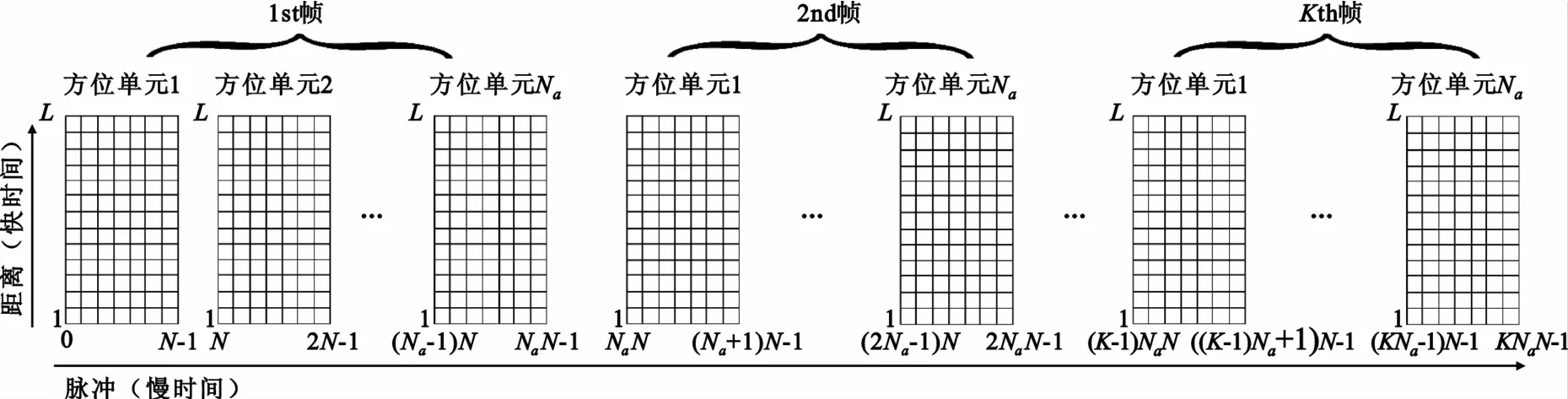
图1 K帧数据的存储格式Fig.1 Storage form of the data during K scans

由于雷达扫描速度较快且目标距离远，假设目标在K帧时间内未跨越方位单元，即在雷达连续扫描期间只在某个特定方位单元上有目标回波。因此，将特定方位单元的回波取出，对其它方位单元的回波置零，形成一个新的数据矩阵，如图2所示，其中对角线所示的阴影区域表示目标所在的方位单元，空白区域表示置零的方位单元。考虑到目标的运动，因此在多帧时间内目标位于不同的距离单元，如图2中实心区域所示，该现象称为距离单元走动。

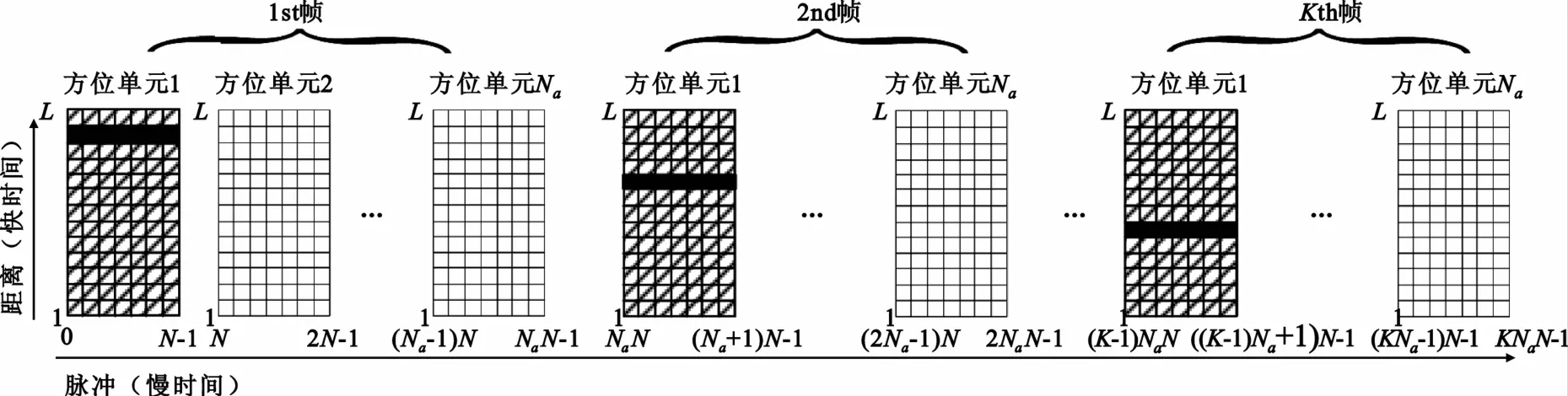
图2 脉冲选取后的数据矩阵Fig.2 Datamatrix after the pulses singled out

令Ω≡{0，1，…，N-1}表示相参脉冲的集合，S≡{1，2，…，L}表示距离单元的集合，ΩT表示目标所在方位单元的集合，ST表示目标所在距离单元的集合，因此，二元检测问题可以写为

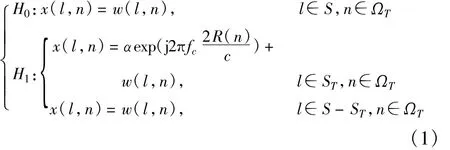
式中，S-ST表示集合S和ST的差，Ω-ΩT表示集合Ω和ΩT的差；α表示目标回波幅度；R（n）表示第n个脉冲时刻目标的距离；fc和c分别为载频和光速；w（l，n）为独立同分布的复高斯噪声，均值为零，方差为σ2w，即w（l，n）～CN（0，σ2w）。公式（1）中，由于慢时间维的时间是连续的，因此利用运动目标回波空-时相关的特性，我们能保留目标的相位信息。对距离R（n）在慢时间n=0处进行二阶Taylor展开得到：

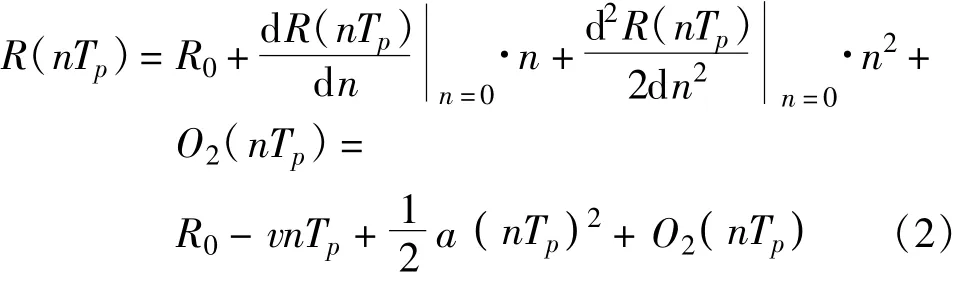
式中，v为目标径向速度，a为径向加速度，R0为n= 0时刻目标的初始位置，O2nT()p为二阶Taylor展开的残差。由于O2nT()p很小，因此可以忽略该项对相位的影响，将式（2）代入式（1）的H1假设中，得到：

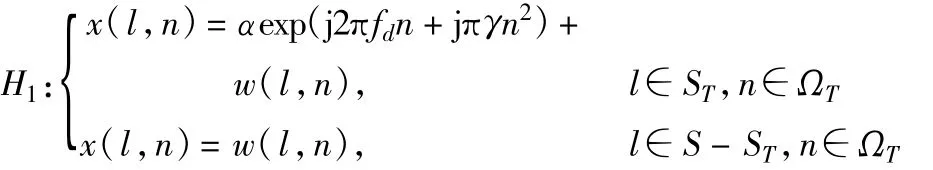
d率，即目标回波为一线性调频（LFM）信号，会出现多普勒单元走动的现象。

上述回波模型有效地保留了目标在多帧时间内的相位信息，使得多帧相参积累成为可能。但是，由于目标回波在多帧时间内可能出现距离单元走动和多普勒单元走动，因此必须进行运动补偿才能实现相参积累。运动补偿意味着要求已知运动目标的参数，而对于非合作目标，其参数是未知的，因此必须采用有效的算法对其进行估计。

3 相参TBD算法

3.1 距离走动校正

雷达接收机对回波信号在快时间维采样并按相应的回波延时将其存放在数据矩阵对应的距离单元中，因此n时刻目标回波所在的距离单元为

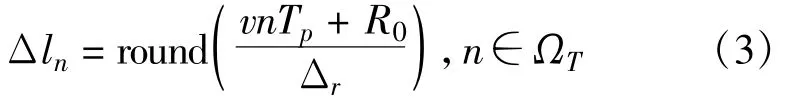
式中，Δr=cτ／2为距离分辨率，τ为发射脉冲宽度，round（·）表示选择最近的整数取整。当积累时间长或者目标速度高使得vnTp＞Δr时，目标回波将跨越距离单元出现距离单元走动的现象，导致无法有效地积累能量，因此必须先进行距离单元走动的补偿。根据公式（3），我们可以对回波进行如下的补偿：

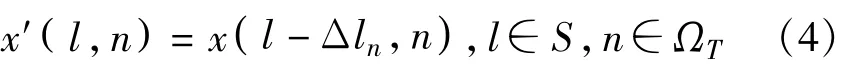
实现上述补偿的前提是已知目标的径向速度v，由于目标的径向速度是未知的，因此需要估计。本文采用速度匹配法来估计目标径向速度，实现距离单元走动校正。在给定的速度范围[Vmin，Vmax]内设定I个速度Vi，i∈I≡{1，2，…，I}，I表示速度的集合。对速度Vi，i∈I≡{1，2，…，I}根据公式3）计算其对应的距离单元走动量Δlin：

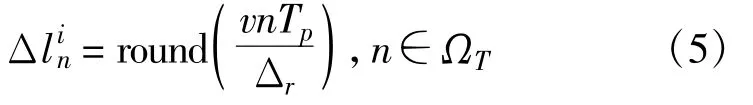
将其代入公式（4）中进行距离单元走动补偿：

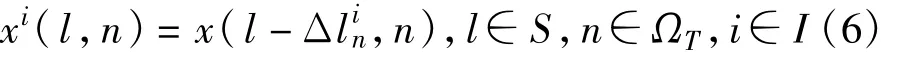
得到I个根据速度Vi进行距离单元走动补偿后的距离-慢时间数据矩阵。如果已知目标多普勒频率，可直接对I个补偿后的距离-慢时间数据矩阵沿其慢时间维进行相位补偿，得到I个L列相参积累的功率输出或幅度输出。假设目标径向速度v= V∈Vi，i∈{}

I，并且n=0时刻目标所在距离单元为l0，那么相参积累的功率输出或幅度输出将在V和l0处取得极大值。由于目标的多普勒频率未知，需要估计，并且目标回波为LFM信号，存在多普勒单元走动的情况，需要估计其调频斜率。下面介绍如何利用DCFT估计多普勒频率和调频斜率，实现相位补偿的方法。

3.2 相位补偿

根据回波模型得到回波信号为LFM信号，对其进行相位补偿需要估计其多普勒频率和调频斜率。DCFT是离散Fourier变换（DFT）的一种推广，它可以同时实现对多普勒频率的估计和调频斜率的估计［9］。对于长度为N的序列，其N点DCFT的定义如下：

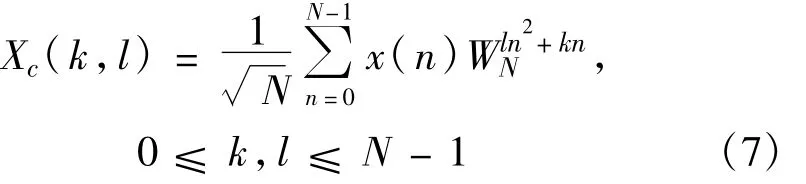
根据DCFT的定义，将I个根据速度Vi进行距离单元走动校正后的距离-慢时间数据矩阵xi( l，n)代入公式（7）中，做N点DCFT：

式中，k、κ分别为调频信号的调频斜率与多普勒频率。因此，zc（i，l，κ，k ）或zc（i，l，κ，k）2在目标参数(V，l0，fd，γ)处有极大值。通过对极大值的提取，可以得到目标相参积累的能量和相应的估计参数。

3.3 算法流程

综上，给出算法流程图如图3所示。

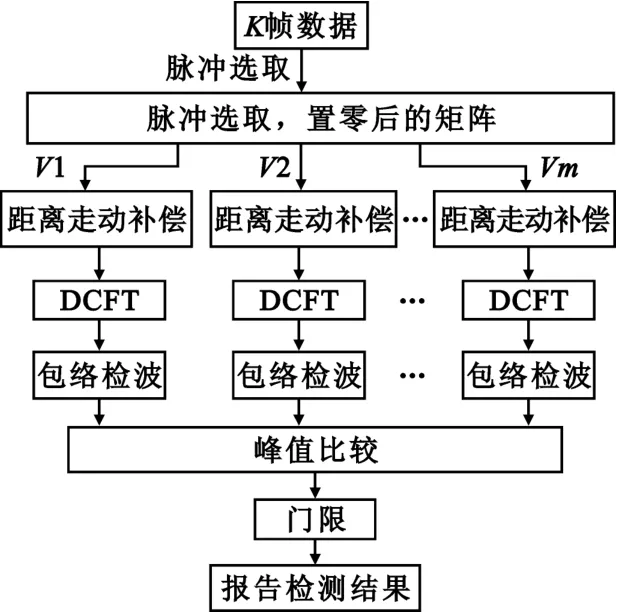
图3 算法流程Fig.3 Flowchart of the proposed algorithm

最后通过将得到的极大值与由虚警概率确定的门限进行比较，得到对目标有无的判断。通过上述流程图可看出，本算法可以对多个速度进行并行化处理，大大减小了速度估计所需的时间。下面我们将采用仿真的方法验证相参回波信号模型的正确性和所提算法参数估计的有效性。

4 仿真实例

设n=0时刻目标位于R0=300 km处，以2 Mach的速度向雷达靠近，其速度与雷达视线方向的夹角为β=60°，如图4所示。雷达系统参数为：雷达发射信号为单频相参信号，载频fc为10 GHz，脉冲重复频率（PRF）为820 Hz，脉宽τ为0.5μs，雷达监视区域被划分为Na=102个方位单元，雷达在每个方位单元上发射M=16个脉冲，完成一次扫描的时间为TR=1.99 s。

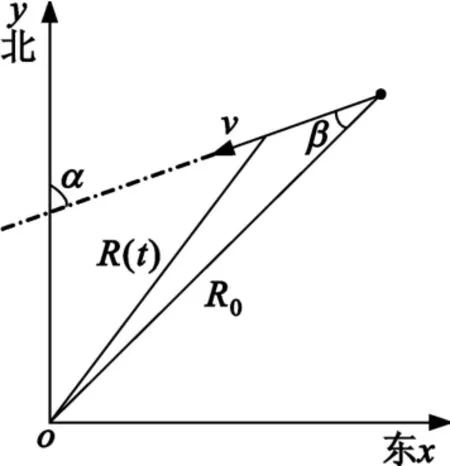
图4 目标运动轨迹Fig.4 Trajectory of an approaching target

信噪比定义为SNR=α2σ／2w。图5给出了K =3帧的回波数据，其中目标回波发生距离走动，回波分别位于95、86和77距离单元处，信噪比为20 dB。图6给出了仅对每帧目标所在方位向的脉冲做相参积累的结果，可以看出目标回波的多普勒走动非常严重。

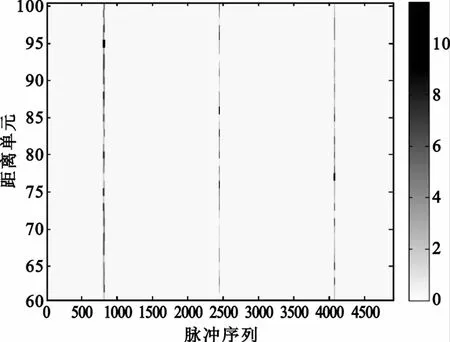
图5 脉冲选取后的数据矩阵，目标回波出现距离单元走动Fig.5 Echoesmigrate across range cell

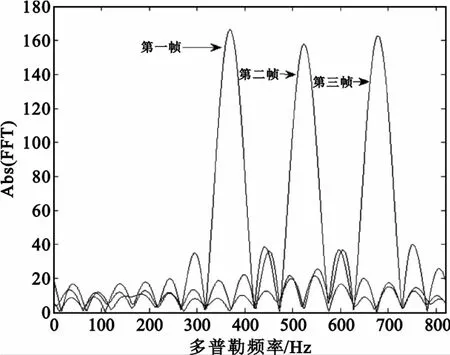
图6 目标所在方位向脉冲相参积累结果Fig.6 Coherent integration of the pulses at targets′azimuth cell

采用本文算法对K=3帧数据进行相参积累，速度范围设为Vmin，V[]max=200，[]1000 m／s，以1 m／s为速度间隔，得到I=801个速度。图7给出了信噪比为-6 dB时最大积累幅度值所在的距离-多普勒平面，该最大积累值即为目标回波积累值，该值远远高于噪声基底，表明了本文算法对目标能量积累的有效性。

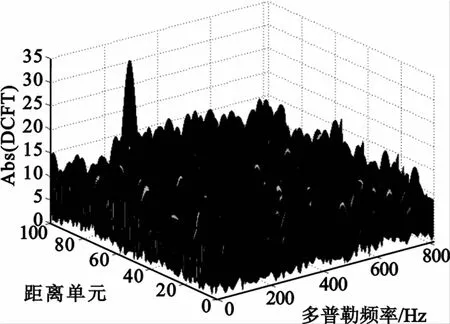
图7 3帧回波数据积累效果图Fig.7 Coherent integration amplitude output using the data of3 scans

图8 给出了采用200次Monte Carlo仿真得到的本文算法的检测性能，其中门限通过Monte Carlo方法求取，虚警概率Pfa=10-6，同样只对K=3帧数据进行联合处理。从图8中可以看出，本文算法采用3帧积累对SNR为-4 dB的目标检测概率能达到80%，而现有的TBD方法均采用6帧及6帧以上数据进行积累以实现对微弱目标的检测及跟踪［3-7］。由于本文算法实现了多帧数据间的相参积累，充分利用了目标的幅度信息和相位信息，因此，本文算法的能量积累效率高于现有的TBD方法，采用较少的帧数就能实现对微弱目标的检测。

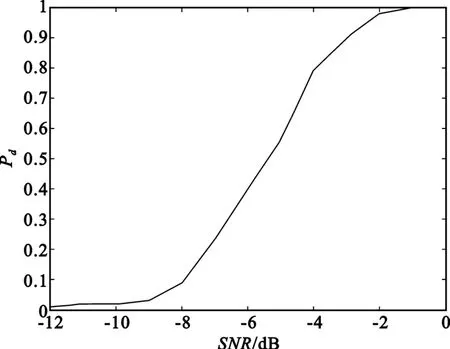
图8 本文算法的检测性能Fig.8 Detection performance of the proposed algorithm

5 结论

针对现有TBD方法在帧与帧之间只利用回波幅度信息而丢弃相位信息实现非相参能量积累导致积累效率低的特点，本文研究了在多帧时间内实现相参积累的TBD方法。利用目标回波的空-时相关性，建立了相参积累的回波模型，针对该模型呈现的特点，提出了一种实现相参积累的TBD算法。通过仿真实验验证了回波模型的正确性和所提算法的有效性。相比于现有TBD方法采用6帧数据积累能量实现对微弱目标的检测和跟踪，本文算法只采用3帧数据就能有效积累能量，实现对微弱目标的检测和跟踪。下一步工作将采用电磁仿真的方法模拟回波数据仿真验证本文算法的有效性。

［1］Carlson BD，Evans ED，Wilson SL.Search radar detection and track with the Hough Transform，PartⅠ：System Concept［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30（1）：102-108.

［2］Wallace W R.The use of track-before-detect in pulse-Doppler radar［C］／／Proceedings of IEEE 2002 International Radar Conference.Edinburgh，UK：IEEE，2002：315-319.

［3］BuzziS，LopsM，Venturino L.Track-before-detectprocedures for early detection ofmoving target from airborne radars［J］.IEEE Transactions on Aerospace and Electronic Systems，2005，41（3）：937-954.

［4］Buzzi S，Lops M，Ferri M.Track-before-detect procedures in a Multi-target environment［J］.IEEE Transactions on Aerospace and Electronic Systems，2008，44（3）：1135-1148.

［5］Rutten MG，Gordon N J，Maskell S.Recursive track-beforedetectwith targetamplitude fluctuations［J］.IEEProceedingsof Radar Sonar Navigation，2005，152（5）：345-322.

［6］Boers Y，Driessen H.Multitarget particle filter track before detect application［J］.IEEProceedingsofRadar Sonar Navigation，2004，151（6）：351-357.

［7］Boers Y，Driessen H，Torstensson J，etal.Track-before-detectalgorithm for tracking extended targets［J］.IEEProceedings of Radar Sonar Navigation，2006，153（4）：345-351.

［8］Richards M.雷达信号处理基础［M］.北京：电子工业出版社，2008. RichardsM.Radar Signal Processing Foundament［M］.Beijing：Publishing House of Electronic Industry，2008.（in Chinese）

［9］Xiang-Gen X.Discrete Chirp-Fourier transform and its application to chirp rate estimation［J］.IEEE Transactions on Signal Processing，2000，48（11）：122-3133.

Track-before-detect M ethod Based on Coherent Integration during M ulti-scan

FAN Ling1，2
（1.School of Physics and Electronic Engineering，Leshan Normal University，Leshan 614004，China；2.School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

A coherent integration track-before-detect（TBD）method is proposed to enhance the ability of detecting low signal-to-noise ratio（SNR）targets.Based on the analysis of themoving targets′echoes during several successive scans，the signalmodel for the coherent TBD is established，in which the targets echoes exhibit range cellmigration and Doppler cell shift.By exploiting the space-time correlation of the

echoes，a lowcomplexity power-efficientalgorithm is proposed.By using velocitymatchingmethod and discrete Chirp-Fourier transform（DCFT），the targets parameters such as target radial velocity，Doppler frequency and chirp rate are jointly estimated to compensate range cellmigration and Doppler cell shift and realize coherent integration.Finally，simulation results show the validity of the signalmodel and the efficiency of the proposed algorithm.

coherent radar；track-before-detect（TBD）；coherent integration；velocitymatching；DCFT

Project Supported by Educational Commission of Sichuan Province of China（07ZB140）；Foundation of Leshan Normal University（Z0820）

TN957.51

A

10.3969／j.issn.1001-893x.2011.07.011

樊玲（1977—），女，四川眉山人，2003年获硕士学位，现为讲师、博士研究生，主要从事雷达信号获取与探测的研究。

1001-893X（2011）07-0050-05

2011-04-07；

2011-06-03

四川省教育厅资助科研项目（07ZB140）；乐山师范学院科研项目（Z0820）

FAN Ling was born in Meishan，Sichuan Province，in 1977. She received the M.S.degree in 2003.She is now a lecturer and currently working toward the Ph.D.degree.Her research concerns detection of radar signal and tracking of radar targets.

Emial：fanling16＠tom.com，lingf＠uestc.edu.cn